Хелпикс

Главная

Контакты

Случайная статья



Практическая работа № 1.. Первичная статистическая обработка экспериментальных данных»



 Практическая работа № 1.

«Первичная статистическая обработка экспериментальных данных»

Задание.Составить вариационный ряд заданных статистических данных. Произвести группировку статистических данных. Найти выборочные числовые характеристики: среднее, дисперсию, среднеквадратическое отклонение, моду, медиану, коэффициент асимметрии, коэффициент эксцесса, максимальную и минимальную порядковые статистики. Построить гистограмму (или полигон). Провести анализ полученных результатов.

 

1). Заполняем таблицу экспериментальных данных

 

Год Их общая площадь, млн. м2
45,2
44,3
40,1
40,1
38,9
35,0
36,1

39,2

39,5

33,9

29,7

28,7
29,5

33,7

36,2

34,7

37,3

37,5

 

2). Упорядочиваем данные в таблице в порядке возрастания значений

Выделяем 2 столбца исходных данных®Меню Сортировка и фильтр ® Настраиваемая сортировка ® Сортировать столбец В, порядок – по возрастанию

 

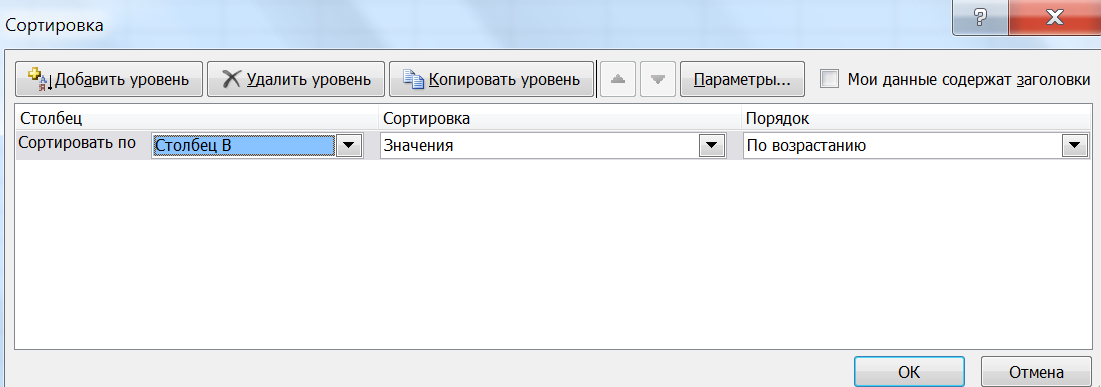
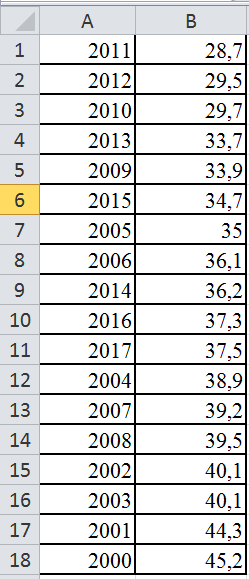
Получаем таблицу, которая называется вариационный ряд:

 

Находим :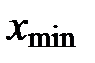

=МИН(B1:B18) ®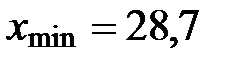

Находим :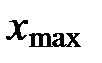

 =МАКС(B1:B18) ®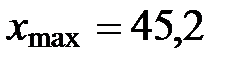

Подсчитываем общее количество данных (строк):

=СЧЁТ(B1:B18) ® n=18

 

3). Находим среднее :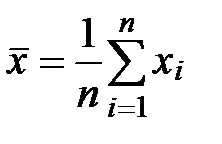

=СРЗНАЧ(B1:B18) ®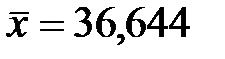

 

4) Находим дисперсию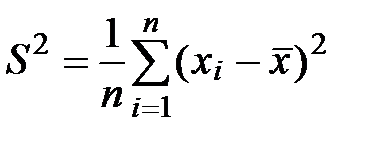

=ДИСПР(B1:B18) ®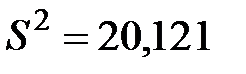  

 

5) Находим среднеквадратичное отклонение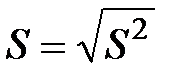

=СТАНДОТКЛОНП(B1:B18) ®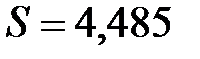

 

6) Находим коэффициент асимметрии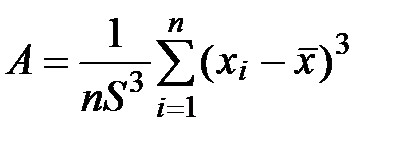

=СКОС(B1:B18) ®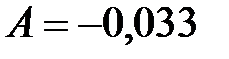

 

Если A = 0, то распределение имеет симметричную форму.

При A > 0 говорят о положительной (или правосторонней) асимметрии.

При A < 0 говорят о отрицательной (или левосторонней) асимметрии.

 

Замечание. Функция СКОС в Excel определяет величину асимметрии по выборочной совокупности, поэтому в ней реализована формула

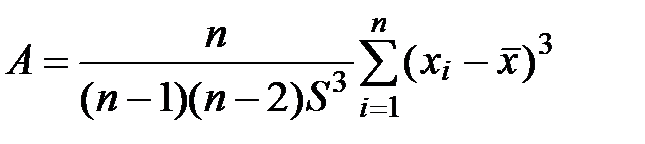
Если данные образуют не выборочную, а генеральную совокупность (как в рассматриваемом примере) то величину асимметрии необходимо рассчитывать по стандартной формуле через центральный момент 3-го порядка и стандартное отклонение по формуле из пункта 6)

 

7) Находим коэффициент эксцесса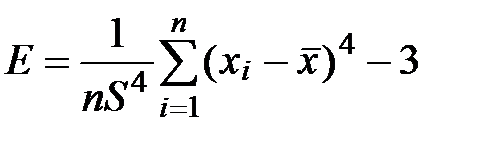

=ЭКСЦЕСС(B1:B18) ®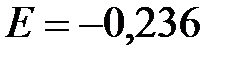

 

Если E > 0, то полигон вариационного ряда имеет более крутую вершину по сравнению с нормальной (гауссовой) кривой.

Если E < 0, то полигон вариационного ряда имеет более пологую вершину по сравнению с нормальной (гауссовой) кривой.

 

Замечание. Функция ЭКСЦЕСС в Excel определяет значение эксцесса по выборочной совокупности, поэтому в ней реализована формула

 

 

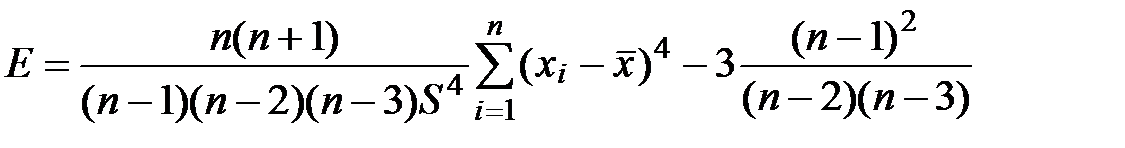
Если данные образуют не выборочную, а генеральную совокупность (как в рассматриваемом примере) то эксцесс необходимо рассчитывать по стандартной формуле через центральный момент 4-го порядка и стандартное отклонение по формуле из пункта 7)

 

 

9). Рассчитываем медиану

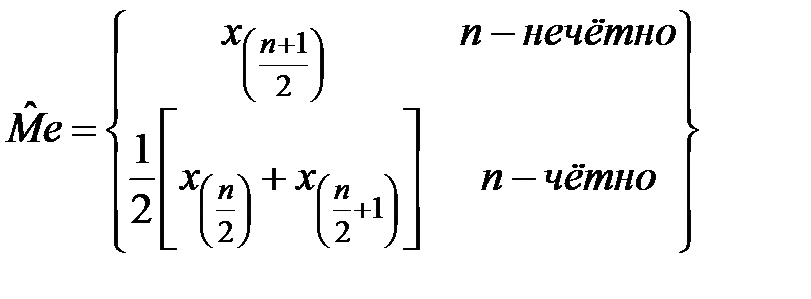
Медиана — это значение, разделяющее некоторое множество чисел на две равные части. Другими словами, половина чисел оказывается больше и половина — меньше медианы.

В Excel можно использовать функцию:

=МЕДИАНА(B1:B18) ®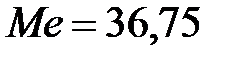

 

10). Упорядоченные по возрастанию данные записываем в виде интервальной таблицы частот. Для этого определяется величина интервала (шага, с которым разбиваются имеющиеся значения). Для этого вычисляем количество интервалов разбиения по формуле:

 

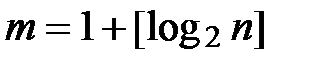
(здесь квадратные скобки обозначают целую часть числа), в Excel для этого можно использовать функцию целое, например, =1+ЦЕЛОЕ(LOG(E1;2))

где E1 – адрес ячейки со значением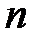

 

или по формуле Стерджеса:

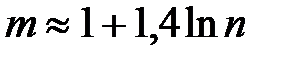 (m округляют до целого числа)

а затем определяем шаг разбиения

,

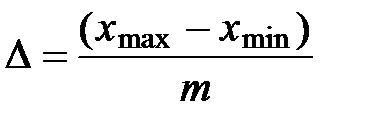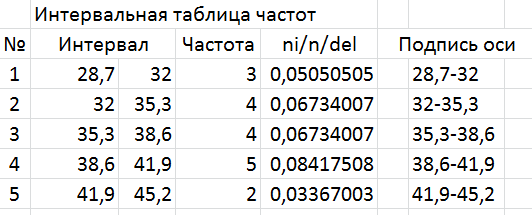
11). Записывается интервальная таблица частот в виде:

 

№ интервала

Интервалы

 Частоты
x min   x1= x min + D n1
x1 x2= x1 + D n2
x2 x3= x2 + D n3
… … … …
m xm-1 xm= xm-1 + D nm

Здесь n1 – число значений из вариационного ряда, попадающее в первый интервал, n2 – число значений из вариационного ряда, попадающее во второй интервал и т.д.

Для данного примера интервальная таблица будет иметь вид:

 

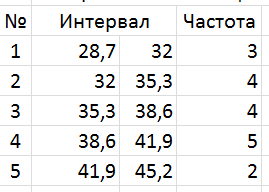
12). Для построения гистограммы используются данные из интервальной таблицы частот. По оси OXоткладывают интервалы шириной D от хmin до хmax. На каждом интервале строят прямоугольник площадью 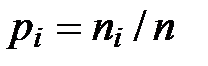 (равной относительной частоте попадания в данный интервал), то есть, высота прямоугольника 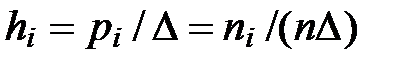. Объединение этих прямоугольников называется гистограммой выборки. Таким образом, площадь каждого прямоугольника гистограммы равна его частоте, а общая площадь равна единице.

 

В Excel для построения гистограммы рассчитывают столбец со значениями 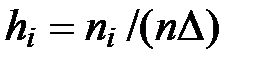 и столбец с указанием границ интервалов, используемый для подписи оси OX.

 

13). Для построения гистограммы из вкладки Вставка используем кнопку Гистограмма

 

 

Далее, нажимая на правую кнопку мыши, выбираем из меню команду Выбрать данные; добавляем ряд, соответствующий значениям 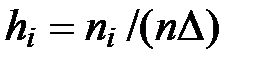; для подписи горизонтальной оси используем рассчитанный выше столбец Подпись оси.

 

14). Мода – выборочное значение, которому соответствует наибольшая частота.

Моду можно найти по простой или интервальной таблице частот.

Моду легко найти графическим путем с помощью гистограммы.

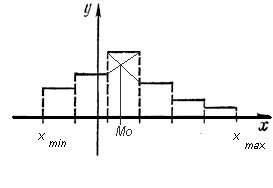
Моду можно рассчитать.

В рассматриваемом примере согласно гистограмме модальным интервалом построенного ряда является интервал 38,6-41,9 так как его частота максимальна (равна 5).

Формула для расчета моды имеет вид:

 

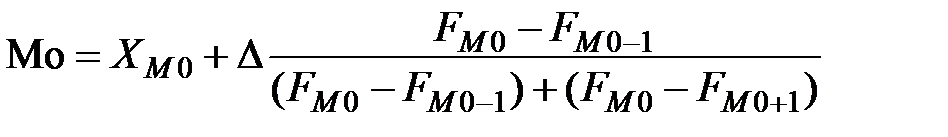=39,425

где

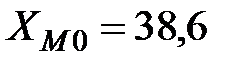 - нижняя граница модального интервала;

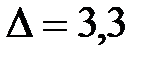 - величина модального интервала;

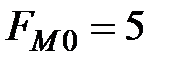 - частота модального интервала;

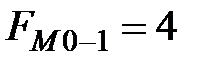 - частота интервала, предшествующего модальному;

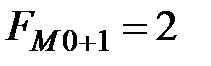 - частота интервала, следующего за модальным.

 

 


Вид отчета

 
  

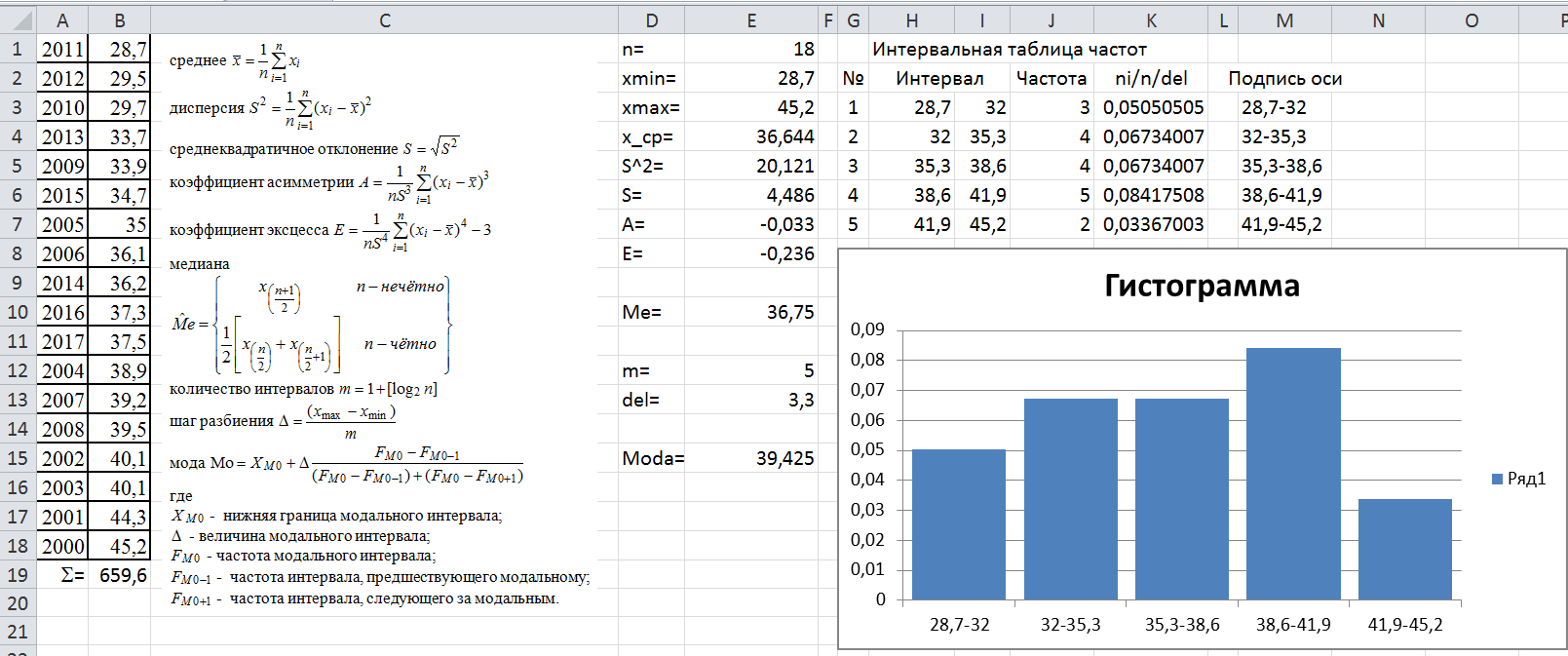
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.