Контакты

Случайная статья

Практическая работа № 3.. Многомерная линейная регрессионная модель»

Практическая работа № 3.

«Многомерная линейная регрессионная модель»

Задание. Определить уравнение множественной линейной регрессии. Оценить качество подгонки и значимость полученного уравнения в целом. Определить среднюю относительную ошибку для построенной модели. Расположить объясняющие факторы по убыванию корреляционной связи с объясняемой переменной. Провести анализ полученных результатов.

Уравнение линейной регрессионной модели будем искать в виде:

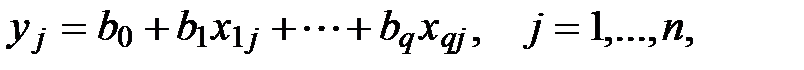
Для этого:

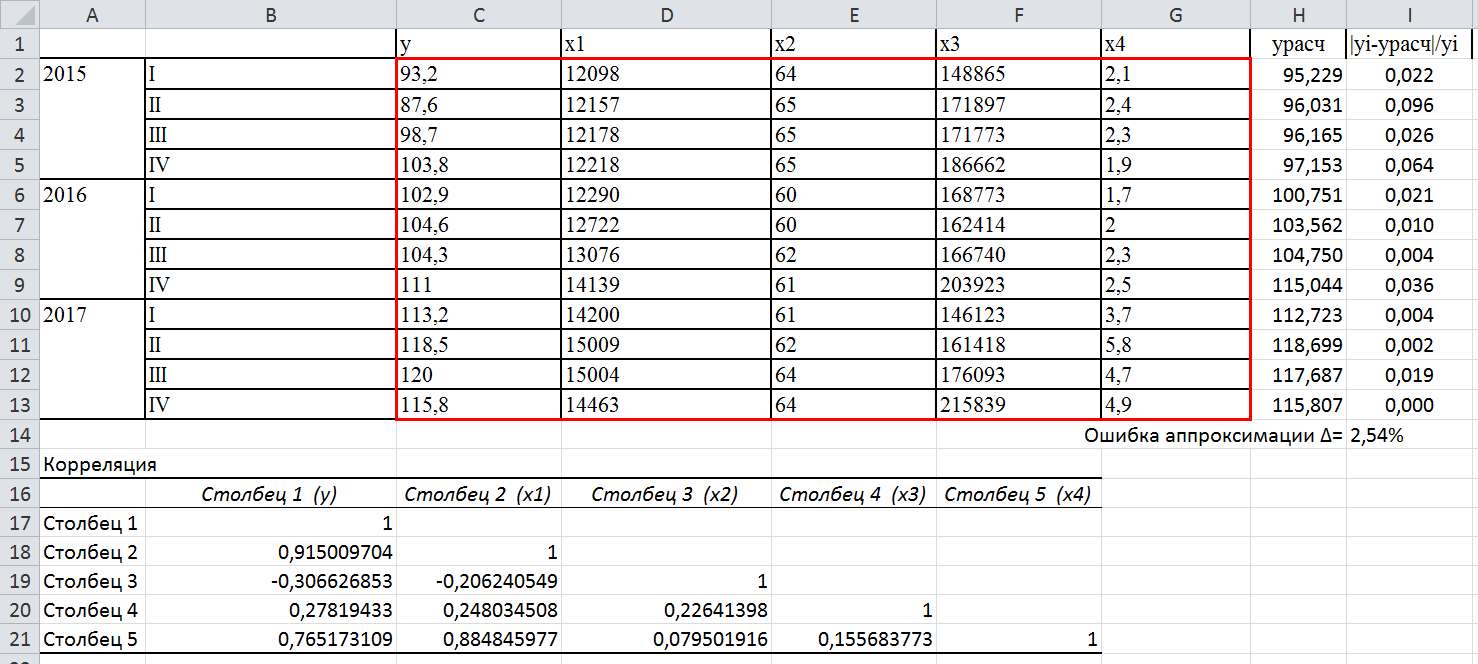
1). Вводим таблицу с данными для своего варианта

		y	x1	x2	x3	x4
	I	93,2				2,1
	II	87,6				2,4
	III	98,7				2,3
	IV	103,8				1,9
	I	102,9				1,7
	II	104,6
	III	104,3				2,3
	IV					2,5
	I	113,2				3,7
	II	118,5				5,8
	III					4,7
	IV	115,8				4,9

Здесь 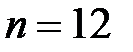(количество строк с данными), 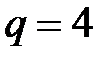(количество факторов )

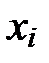2) Расчет коэффициентов корреляции в Excel с помощью пакета «Анализ данных».

Меню: Данные®Анализ данных®Корреляция

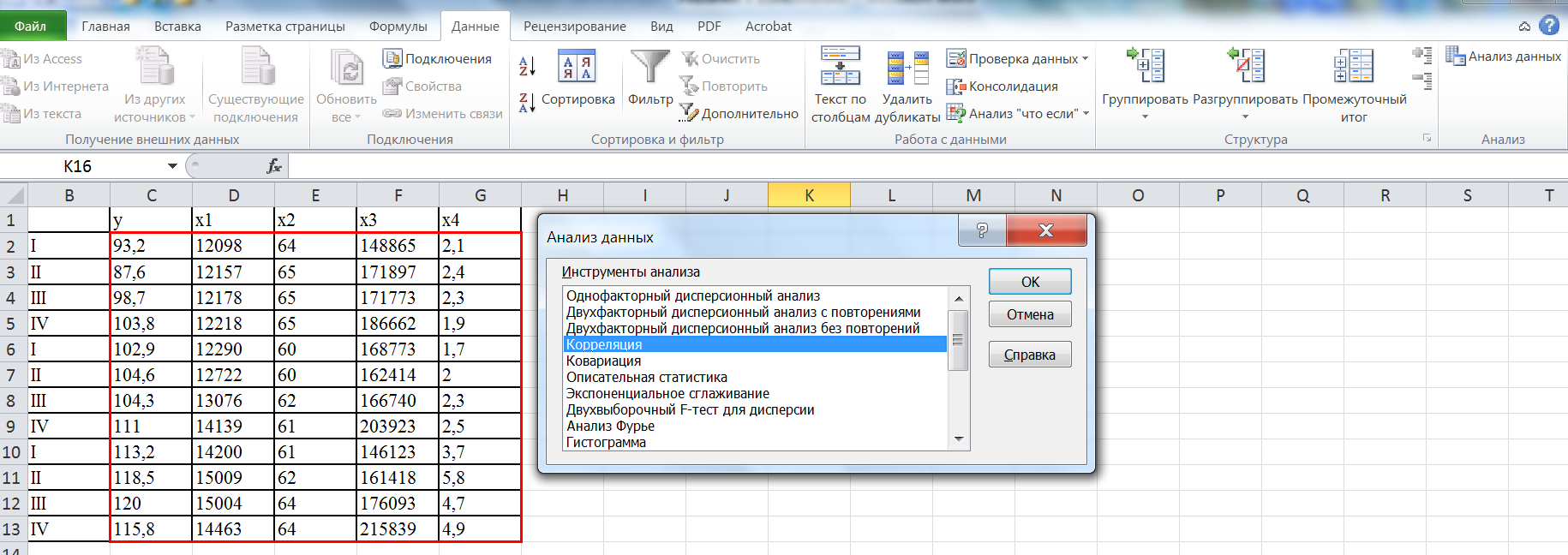
Если пакет анализ данных отсутствует, его надо установить:

Меню Файл®Параметры®Надстройки®Пакет анализа®Перейти (применить) ® Пакет анализа®OK

Ввод данных:

входной интервал: выделить область с данными

выходной интервал: любая свободная ячейка (или новый лист)

В результате получаем таблицу корреляции:

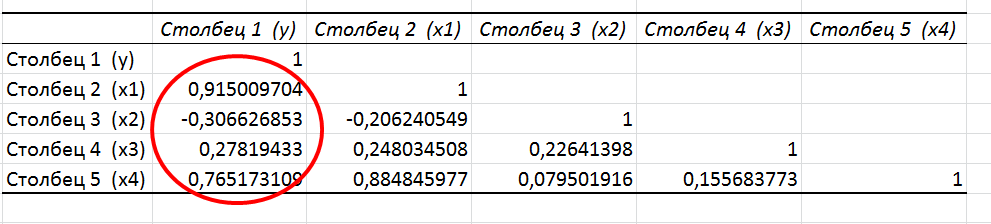
Коэффициенты корреляции из таблицы:

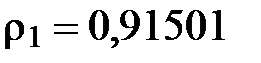
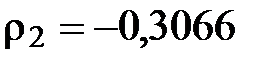
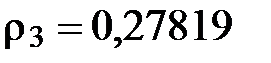
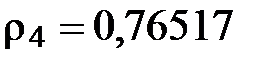
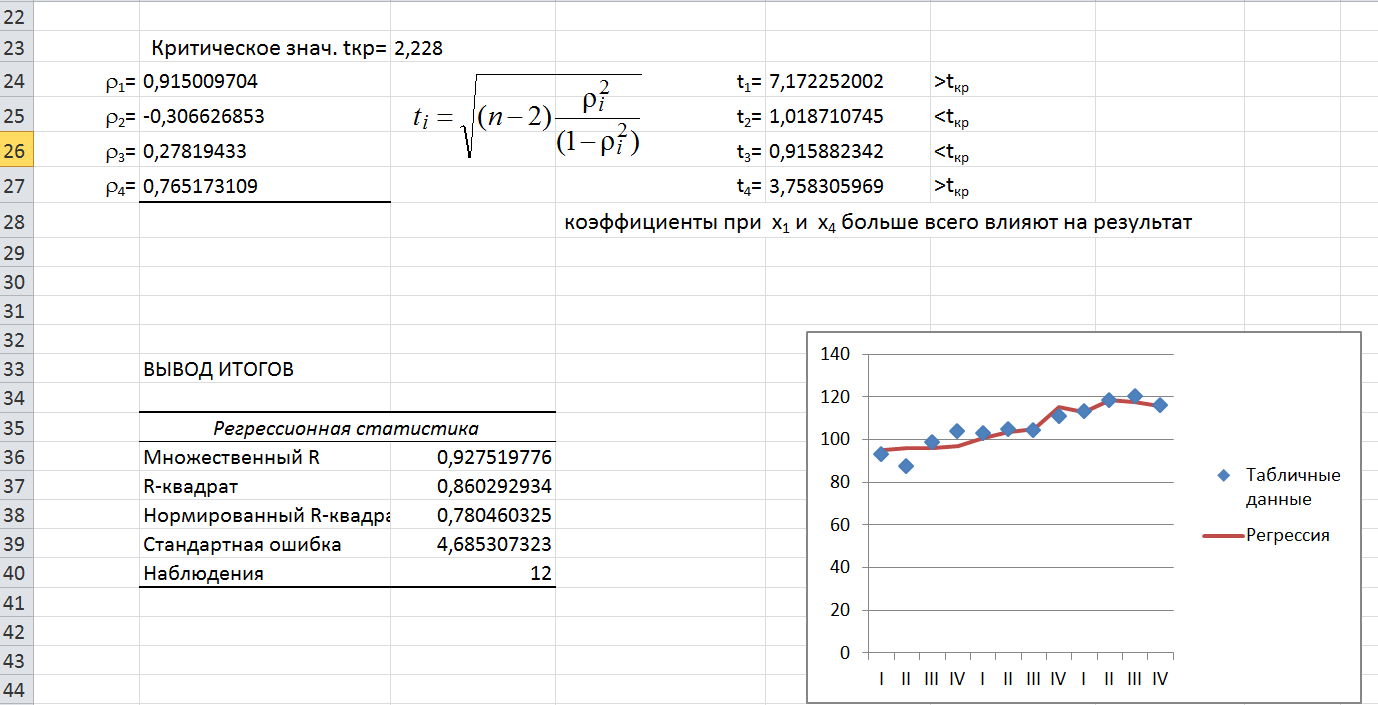
3). Проверка значимости коэффициентов по критерию Стьюдента:

рассчитываются значения 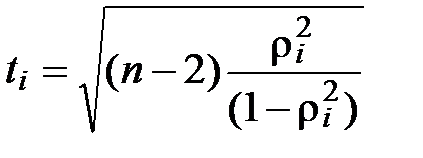, где 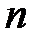– число данных ( 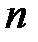=12 для данного примера)

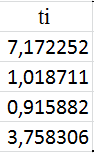
4). Вычисляем 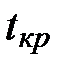с помощью функции обратного распределения Стьюдента:

=СТЬЮДРАСПОБР( α; n-2) = СТЬЮДРАСПОБР(0,05;10)

Получаем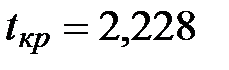

Из всех коэффициентов 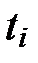выбираем те, которые .

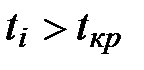В данном примере:

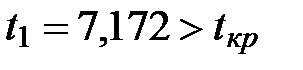
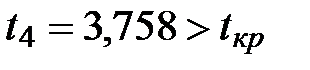
Вывод: коэффициенты пр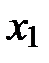и и 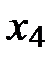больше всего влияют на результат.

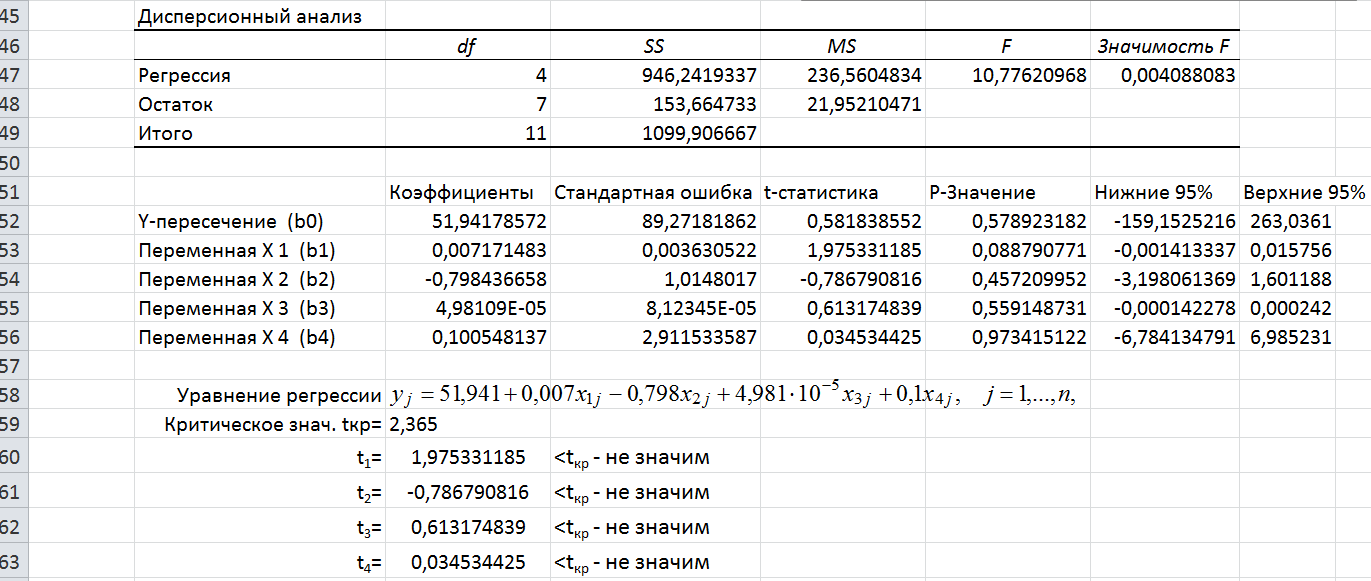
5). Построение многомерной регрессии

Меню: Данные®Анализ данных®Регрессия

входной интервал Y: столбец значений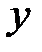

выходной интервал X: столбцы , , ,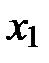

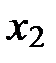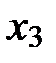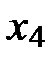
выходной интервал: любая свободная ячейка (или новый лист)

В результате получаем таблицу для коэффициентов регрессии , , , ,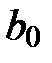

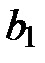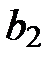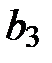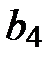
и t- статистику

Поэтому в данном примере уравнение линейной регрессии имеет вид:

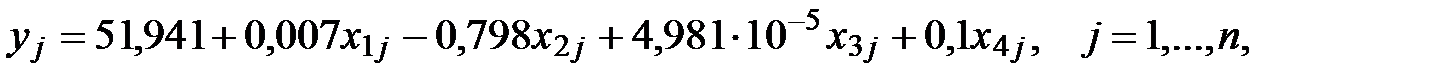
Проверка значимости коэффициентов также может быть реализована с помощью функции:

= СТЬЮДРАСПОБР( α; n-m-1)

В рассматриваемом примере n=12, m=4, α возьмем равным 0,05.

= СТЬЮДРАСПОБР(0,05;7)

Получаем .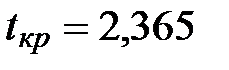

Если 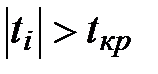то коэффициенты значимые.

t- статистика:

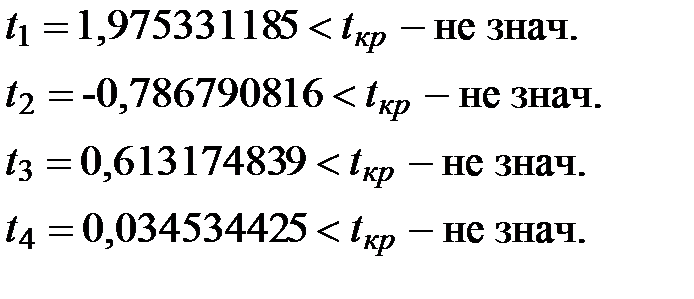
6). При заданных значениях 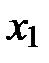, , 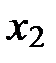, 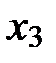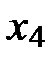(из условий задания) и полученных коэффициентов регрессии 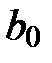, , 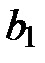, , 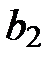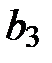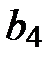вычисляем

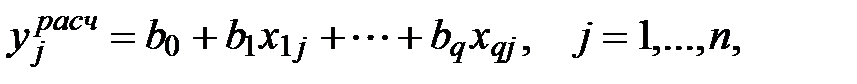
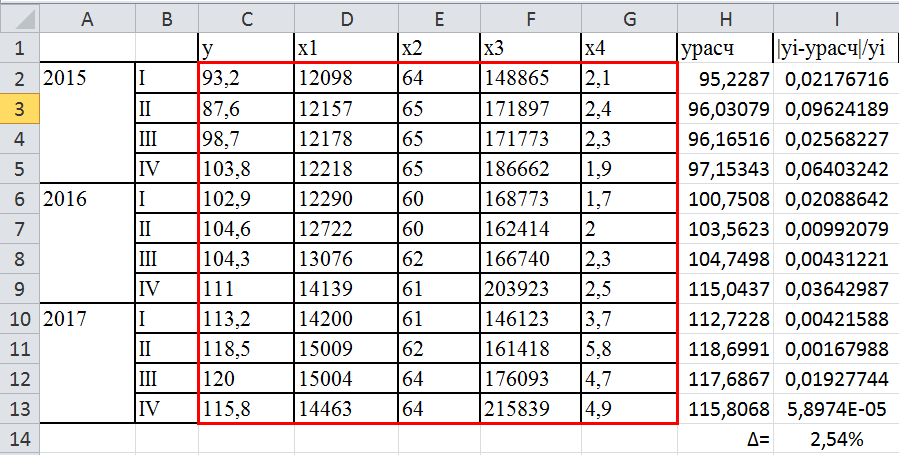
Здесь ∆ – средняя ошибка аппроксимации вычислялась по формуле:

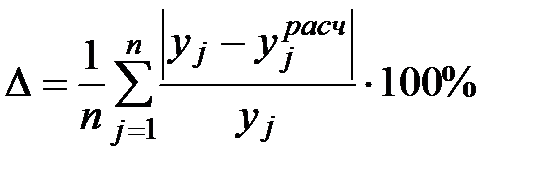
Замечание. В Excel можно не умножать на 100%, а применить к ячейке с результатом формат «процентный»

7). Строим график функции 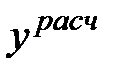, там же наносим данные для 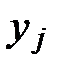, взятых из таблицы с исходными данными.

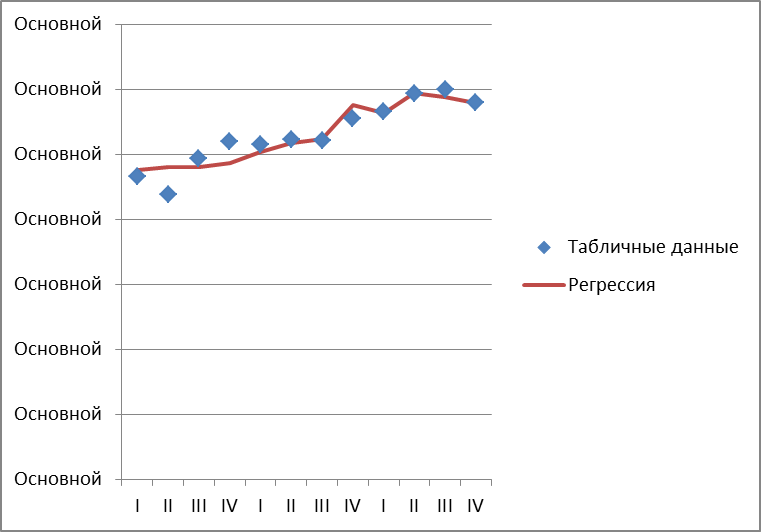
Уравнение линейной регрессии: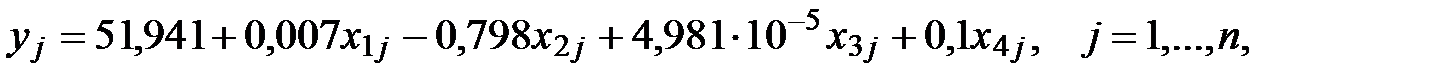

Вид отчета

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.