Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Банк открытых заданий по геометрии для промежуточной аттестации.

Банк открытых заданий по геометрии для промежуточной аттестации.

ЧАСТЬ 1

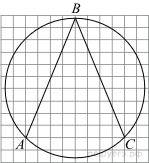
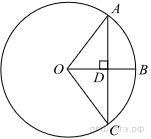
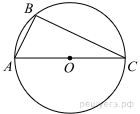
1.Найдите угол ABC. Ответ дайте в градусах.

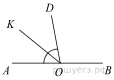
2. Найдите ве­ли­чи­ну угла DOK, если OK — бис­сек­три­са угла AOD, ∠DOB = 108°. Ответ дайте в градусах.

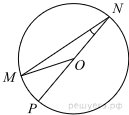
3. Найдите гра­дус­ную меру центрального ∠MON, если известно, NP — диаметр, а гра­дус­ная мера ∠MNP равна 18°.

4.Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.

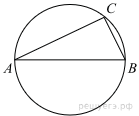
5.Найдите угол ABC. Ответ дайте в градусах.

6.Укажите но­ме­ра верных утверждений.

1) Бис­сек­три­са равнобедренного треугольника, проведённая из вершины, про­ти­во­ле­жа­щей основанию, делит ос­но­ва­ние на две рав­ные части.

2) В любом пря­мо­уголь­ни­ке диагонали вза­им­но перпендикулярны.

3) Для точки, ле­жа­щей на окружности, рас­сто­я­ние до цен­тра окружности равно радиусу.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

7.Медиана равностороннего треугольника равна 9√3. Найдите сторону этого треугольника.

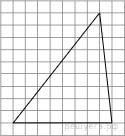
8. Найдите гра­дус­ную меру ∠ACB, если известно, что BC яв­ля­ет­ся диа­мет­ром окружности, а гра­дус­ная мера центрального ∠AOC равна 96°.

9. В пря­мо­уголь­ни­ке диагональ равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны 5√3. Най­ди­те площадь прямоугольника, деленную на √3.

10. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние от точки А до пря­мой ВС. Ответ вы­ра­зи­те в сантиметрах.

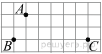
 11.Укажите но­ме­ра верных утверждений.

1) Цен­тры вписанной и опи­сан­ной окружностей рав­но­сто­рон­не­го треугольника совпадают.

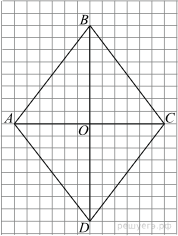
2) Су­ще­ству­ет квадрат, ко­то­рый не яв­ля­ет­ся ромбом.

3) Сумма углов лю­бо­го треугольника равна 180° .

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

12.В треугольнике АВС известно, что АС=54, ВМ - медиана, ВМ=43. Найдите АМ.

13.В окруж­но­сти с цен­тром O AC и BD — диаметры. Угол ACB равен 26°. Най­ди­те угол AOD. Ответ дайте в градусах.

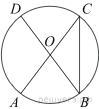
14.Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше другой.

15.На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние от точки А до се­ре­ди­ны от­рез­ка ВС. Ответ вы­ра­зи­те в сантиметрах.

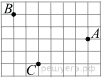
16.Укажите номера верных утверждений.

1) Если угол острый, то смежный с ним угол также является острым.

2) Диагонали квадрата взаимно перпендикулярны.

3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

17.Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 66, сторона BC равна 37, сторона AC равна 74. Найдите MN.

18. Прямоугольный тре­уголь­ник с ка­те­та­ми 5 см и 12 см впи­сан в окружность. Чему равен ра­ди­ус этой окружности?

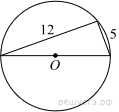
19.Найдите пло­щадь параллелограмма, изображённого на рисунке.

20.На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1x1 изображён тре­уголь­ник ABC. Най­ди­те длину его высоты, опу­щен­ной на сто­ро­ну AC.

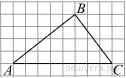
21. Укажите но­ме­ра верных утверждений.

1) Если три сто­ро­ны одного тре­уголь­ни­ка пропорциональны трём сто­ро­нам другого треугольника, то тре­уголь­ни­ки подобны.

2) Сумма смеж­ных углов равна 180°.

3) Любая вы­со­та равнобедренного тре­уголь­ни­ка является его биссектрисой.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

22. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 196, а ос­но­ва­ние — 96. Най­ди­те пло­щадь тре­уголь­ни­ка.

23. Радиус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окружности равен 5 см.

24. Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

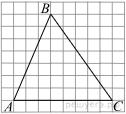
25. На клетчатой бумаге с размером клетки 1х1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АС

.

26. Какие из следующих утверждений верны?

1) Если угол равен 45°, то вертикальный с ним угол равен 45°.

2) Любые две прямые имеют ровно одну общую точку.

3) Через любые три точки проходит ровно одна прямая.

4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.

27.Медиана равностороннего треугольника равна 11√3. Найдите сторону этого треугольника.

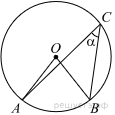
28.Найдите ве­ли­чи­ну (в градусах) впи­сан­но­го угла α, опи­ра­ю­ще­го­ся на хорду AB, рав­ную ра­ди­у­су окружности.

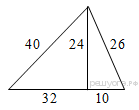
29.Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ражённого на ри­сун­ке.

30.Най­ди­те тангенс угла А тре­уголь­ни­ка ABC, изображённого на рисунке.

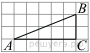
31.Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

32. В треугольнике АВС известно, что АВ=ВС, угол АВС равен 148°. Найдите угол ВСА. Ответ дайте в градусах.

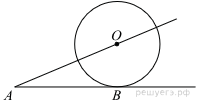
33. К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и секущая AO. Най­ди­те ра­ди­ус окружности, если AB = 12 см, AO = 13 см.

34. Сторона рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на √3.

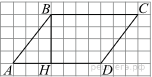
35. На ри­сун­ке изображен па­рал­ле­ло­грамм АВСD. Ис­поль­зуя рисунок, найди­те sin˪HBA

.

36. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние на­крест ле­жа­щие углы со­став­ля­ют в сумме 90°, то эти две пря­мые параллельны.

2) Если угол равен 60°, то смеж­ный с ним равен 120°.

3) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние од­но­сто­рон­ние углы равны 70° и 110°, то эти две пря­мые параллельны.

4) Через любые три точки про­хо­дит не более одной прямой.

Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

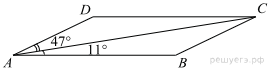
37. В па­рал­ле­ло­грам­ме ABCD про­ве­де­на диа­го­наль AC. Угол DAC равен 47°, а угол CAB равен 11°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD. Ответ дайте в градусах.

38. На окружности с центром O отмечены точки A и B так, что ∠AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.

39. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.

40. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

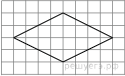
41. Какие из следующих утверждений верны?

1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.

3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

Если утверждений несколько, запишите их номера в порядке возрастания.

42.Найдите ве­ли­чи­ну остро­го угла па­рал­ле­ло­грам­ма ABCD, если бис­сек­три­са угла A об­ра­зу­ет со сто­ро­ной BC угол, рав­ный 15°. Ответ дайте в градусах.

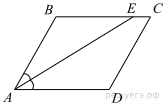
43. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

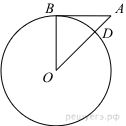
44. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

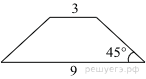
45. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

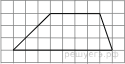
46. Какие из следующих утверждений верны?

1) Через любые три точки проходит не более одной окружности.

2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Если утверждений несколько, запишите их номера в порядке возрастания.

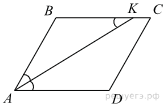
47.Биссектриса угла A па­рал­ле­ло­грам­ма ABCD пе­ре­се­ка­ет сто­ро­ну BC в точке K. Най­ди­те пе­ри­метр параллелограмма, если BK = 6, CK = 10.

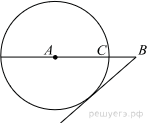
48. На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

49. Радиус круга равен 1. Найдите его площадь, деленную на π.

50. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

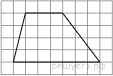
51. Какие из следующих утверждений верны?

1) Сумма углов выпуклого четырехугольника равна 180°.

2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

3) Диагонали квадрата делят его углы пополам.

4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

Если утверждений несколько, запишите их номера в порядке возрастания.

52.Точка O — центр окружности, на ко­то­рой лежат точки P, Q и R таким образом, что OPQR — ромб. Най­ди­те угол ORQ. Ответ дайте в градусах.

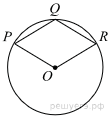
53. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

54. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.

55. Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

56. Какие из следующих утверждений верны?

1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.

4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

Если утверждений несколько, запишите их номера в порядке возрастания.

57.Сто­ро­на ромба равна 36, а ост­рый угол равен 60°. Вы­со­та ромба, опу­щен­ная из вер­ши­ны ту­по­го угла, делит сто­ро­ну на два от­рез­ка. Ка­ко­вы длины этих от­рез­ков? Перечислите эти длины в от­ве­те без пробелов в по­ряд­ке возрастания.

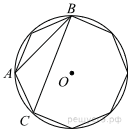
58. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

59. Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.

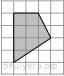
60. Какие из следующих утверждений верны?

1) Около всякого треугольника можно описать не более одной окружности.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Если утверждений несколько, запишите их номера в порядке возрастания.

61. Найдите боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной AB углы, рав­ные 30° и 45° соответственно.

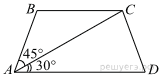
62. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

63. На клетчатой бумаге с размером клетки 1x1 изображена фигура. Найдите её площадь.

64. Какие из следующих утверждений верны?

1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4) Около любого ромба можно описать окружность.

Если утверждений несколько, запишите их номера в порядке возрастания.

65. Найдите угол ABC рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной CD углы, рав­ные 30° и 80° соответственно.

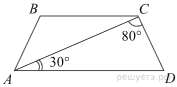
66. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.

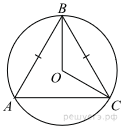
67. Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.

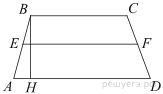
68. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

69. Какие из следующих утверждений верны?

1) Окружность имеет бесконечно много центров симметрии.

2) Прямая не имеет осей симметрии.

3) Правильный пятиугольник имеет пять осей симметрии.

4) Квадрат не имеет центра симметрии.

Если утверждений несколько, запишите их номера в порядке возрастания.

70. В  рав­но­бед­рен­ной тра­пе­ции из­вест­ны вы­со­та,  мень­шее ос­но­ва­ние и угол при ос­но­ва­нии. Най­ди­те боль­шее ос­но­ва­ние.

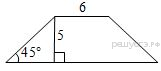
71. AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.

72. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.

73. На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.

74. Какие из следующих утверждений верны?

1) Правильный шестиугольник имеет шесть осей симметрии.

2) Прямая не имеет осей симметрии.

3) Центром симметрии ромба является точка пересечения его диагоналей.

4) Равнобедренный треугольник имеет три оси симметрии.

Если утверждений несколько, запишите их номера в порядке возрастания.

75. Около тра­пе­ции, один из углов ко­то­рой равен 49°, опи­са­на окруж­ность. Най­ди­те осталь­ные углы тра­пе­ции. Запишите ве­ли­чи­ны углов в ответ без пробелов в по­ряд­ке убывания.

76. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

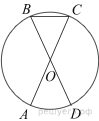
77. Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.

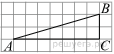
78. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.

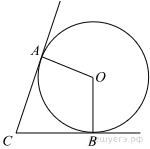
79. Какие из следующих утверждений верны?

1) Центром симметрии прямоугольника является точка пересечения диагоналей.

2) Центром симметрии ромба является точка пересечения его диагоналей.

3) Правильный пятиугольник имеет пять осей симметрии.

4) Центром симметрии равнобедренной трапеции является точка пересечения ее диагоналей.

Если утверждений несколько, запишите их номера в порядке возрастания.

80. Углы вы­пук­ло­го че­ты­рех­уголь­ни­ка от­но­сят­ся как 1:2:3:4. Най­ди­те мень­ший угол. Ответ дайте в градусах.

81. Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 115°.

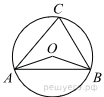
82.Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.

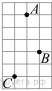
83. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

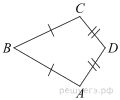
84. Какие из следующих утверждений верны?

1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

2) Любые два равнобедренных треугольника подобны.

3) Любые два прямоугольных треугольника подобны.

4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Если утверждений несколько, запишите их номера в порядке возрастания.

85. В вы­пук­лом че­ты­рех­уголь­ни­ке ABCD AB = BC, AD = CD, ∠B = 77°, ∠D = 141°. Най­ди­те угол A. Ответ дайте в градусах.

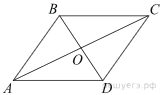
86. Сторона AC треугольника ABC содержит центр описанной около него окружности. Найдите ∠С, если ∠А=75°. Ответ дайте в градусах.

87. Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.

88. На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

89. Какие из следующих утверждений верны?

1) Любые два прямоугольных треугольника подобны.

2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

3) Стороны треугольника пропорциональны косинусам противолежащих углов.

4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Если утверждений несколько, запишите их номера в порядке возрастания.

90. Сумма двух углов равнобедренной трапеции равна 218⁰. Найдите меньший угол трапеции. Ответ дайте в градусах.

91. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.

92. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.

93. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg CDO

94. Какие из следующих утверждений верны?

1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.

2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.

3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.

4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.

Если утверждений несколько, запишите их номера в порядке возрастания.

ЧАСТЬ 2

1.Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .

2.Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28.

3. В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6, BC = 8 . Найдите медиану CK этого треугольника.

4. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.

5. Найдите площадь трапеции, диагонали которой равны 16 и 12, а средняя линия равна 10.

6. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 19, а расстояние от точки K до стороны AB равно 7.

7. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 7.

8. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.

9. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.

10. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 6, а сторона AC в 1,5 раза больше стороны BC.