
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Производной функции в точке называют предел отношения приращения функции в точке к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует.
Касательная к графику функции и производная с примерами решения
Вы уже знаете, какую прямую называют касательной к окружности. А что понимают, например, под касательной к синусоиде? Прямая 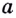
Пусть даны график функции 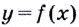 и на ней точка
и на ней точка 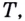 которая не является концом графика (рис. 60). Обозначим на данном графике по разные стороны от
которая не является концом графика (рис. 60). Обозначим на данном графике по разные стороны от 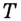 произвольные точки
произвольные точки 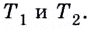 Прямые
Прямые 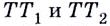 — секущие. Если же точки
— секущие. Если же точки 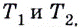 двигаясь по графику, приближать достаточно близко к
двигаясь по графику, приближать достаточно близко к 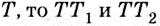 как угодно близко будут приближаться к некоторой прямой
как угодно близко будут приближаться к некоторой прямой 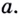 Такую прямую
Такую прямую 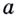 (если она существует) называют касательной к графику функции
(если она существует) называют касательной к графику функции  в точке
в точке 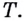
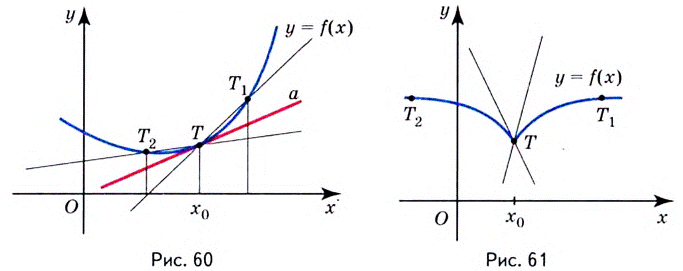
Если график функции такой, как показано на рисунке 61, то при неограниченном приближении точек 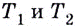 к точке
к точке 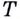 предельные положения секущих — прямые
предельные положения секущих — прямые 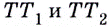 — не совпадут. Говорят, что в точке
— не совпадут. Говорят, что в точке  касательной к графику функции не существует.
касательной к графику функции не существует.

И если 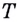 — крайняя точка графика, то касательной к нему в точке
— крайняя точка графика, то касательной к нему в точке 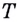 не существует.
не существует.
Понятие касательной к графику часто используют для исследования функций. Рассмотрим этот вопрос сначала в общем виде.
Касательная — это прямая. Её уравнение имеет вид 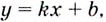 где
где 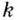 — угловой коэффициент — тангенс угла между лучом касательной, расположенным выше оси
— угловой коэффициент — тангенс угла между лучом касательной, расположенным выше оси 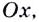 и положительным направлением этой оси. Обратите внимание на угловой коэффициент
и положительным направлением этой оси. Обратите внимание на угловой коэффициент 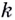 касательной, проведённой к графику какой-либо функции в его точке с абсциссой
касательной, проведённой к графику какой-либо функции в его точке с абсциссой  Если число
Если число 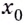 принадлежит промежутку возрастания функции, то соответствующее значение
принадлежит промежутку возрастания функции, то соответствующее значение  положительное (рис. 62). Если
положительное (рис. 62). Если 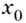 принадлежит промежутку убывания функции, то
принадлежит промежутку убывания функции, то 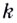 — отрицательное (рис. 63). И наоборот: если каждому значению
— отрицательное (рис. 63). И наоборот: если каждому значению 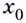 из некоторого промежутка
из некоторого промежутка 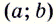 соответствует положительное значение
соответствует положительное значение 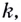 то на
то на 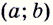 данная функция возрастает; если каждому значению
данная функция возрастает; если каждому значению 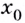 из некоторого промежутка
из некоторого промежутка  соответствует отрицательное значение
соответствует отрицательное значение 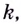 то на функция убывает. Заслуживают внимания и те точки графика функции, в которых касательная не существует, и в которых она параллельна оси
то на функция убывает. Заслуживают внимания и те точки графика функции, в которых касательная не существует, и в которых она параллельна оси 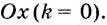

Итак, зная угловые коэффициенты касательных к графику функции в тех или иных точках, можно сделать вывод, возрастает данная функция в этих точках, или убывает.
Поскольку для исследования функций важно уметь определять угловой коэффициент касательной к её графику, то рассмотрим подробнее связь этого коэффициента с исследуемой функцией.
Пусть даны график функции 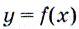 и на ней точку
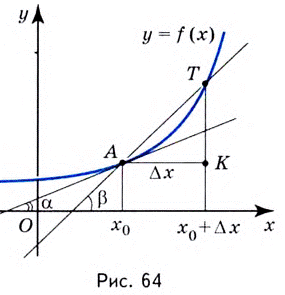
и на ней точку 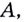 в которой существует касательная к графику (рис. 64). Если абсцисса точки
в которой существует касательная к графику (рис. 64). Если абсцисса точки 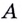 равна
равна 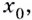 то её ордината —
то её ордината — 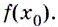 Дадим значению аргумента
Дадим значению аргумента 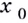 приращение
приращение 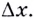 Тогда значению аргумента
Тогда значению аргумента 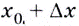 на графике функции соответствует точка
на графике функции соответствует точка  с абсциссой
с абсциссой 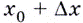 и ординатой
и ординатой 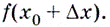
Через точки 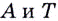 проведём прямые
проведём прямые 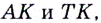 параллельные осям абсцисс и ординат. Они пересекутся в некоторой точке
параллельные осям абсцисс и ординат. Они пересекутся в некоторой точке 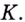 Тогда
Тогда 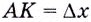 — приращение аргумента, а
— приращение аргумента, а 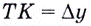 — приращение функции на
— приращение функции на 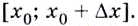
Угловой коэффициент секущей  равен тангенсу угла
равен тангенсу угла 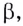 т. е. отношению
т. е. отношению 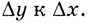
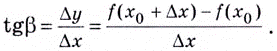
Если  то секущая
то секущая 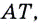 поворачиваясь вокруг точки
поворачиваясь вокруг точки 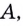 приближается к касательной, проведённой в точке
приближается к касательной, проведённой в точке 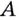 к графику данной функции. Итак, если
к графику данной функции. Итак, если 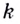 — угловой коэффициент этой касательной и
— угловой коэффициент этой касательной и 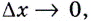 то
то
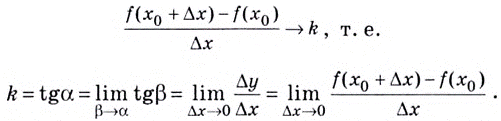
Так определяется угловой коэффициент касательной к графику функции 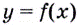 в некоторой точке
в некоторой точке 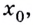 если касательная в ней не параллельна оси
если касательная в ней не параллельна оси 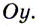 Если касательная к графику функции в некоторой точке параллельна оси
Если касательная к графику функции в некоторой точке параллельна оси 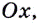 то угловой коэффициент этой касательной равен нулю.
то угловой коэффициент этой касательной равен нулю.
К вычислению значения выражения 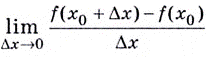 или
или  приводит решение многих задач по механике, электричеству, биологии, экономике, статистике и т. д. Именно поэтому это выражение получило специальное название — производная.
приводит решение многих задач по механике, электричеству, биологии, экономике, статистике и т. д. Именно поэтому это выражение получило специальное название — производная.
Производной функции в точке называют предел отношения приращения функции в точке к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует.
Производную функции 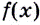 в точке
в точке 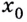 обозначают
обозначают 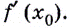 Её определение записывают также в виде равенства:
Её определение записывают также в виде равенства:
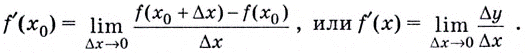
Пример:
Найдите производную функции 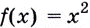 в точке
в точке 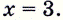
Решение:
Дадим аргументу 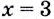 приращение
приращение 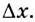 Соответствующее приращение функции
Соответствующее приращение функции 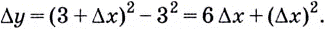
Тогда 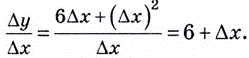 Если
Если 
Следовательно, 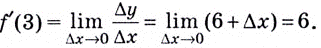
Ответ. 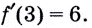
Так решают задачу, пользуясь определением производной функции в точке.
До сих пор речь шла о производной функции в точке. А можно рассматривать производную функции и как функцию. Пусть, например, дана функция  Найдём её производную в произвольной точке
Найдём её производную в произвольной точке 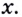 Для этого дадим значению
Для этого дадим значению  приращение
приращение 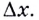 Соответствующее ему приращение функции
Соответствующее ему приращение функции
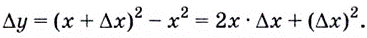
Поэтому 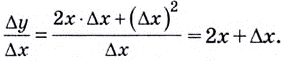 Если
Если 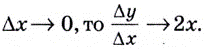
Имеем 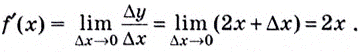
Следовательно, производная функции 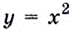 в каждой её точке
в каждой её точке 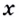 равна
равна 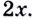 Пишут:
Пишут: 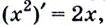 или, если
или, если 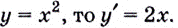
Обратите внимание! Производная функции в точке — это число. Когда же говорят о производной, не указывая «в точке», подразумевают производную как функцию: производной функции 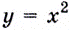 есть функция
есть функция 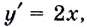 производной функции
производной функции 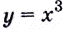 есть функция
есть функция 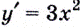 и т. д.
и т. д.
Зная это, производную функции в точке можно вычислять проще, чем по определению производной функции в точке. Пример 2. Дана функция 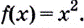 Найдите
Найдите 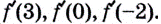 Решение. Производной функции
Решение. Производной функции 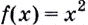 является функция
является функция 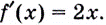 Поэтому
Поэтому 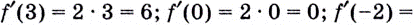
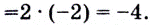
Нахождение производной называется дифференцированием. Функция, которая имеет производную в точке называется дифференцируемой в точке Функция, дифференцируемая в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.
Докажем, например, что линейная функция 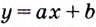 дифференцируема в каждой точке
дифференцируема в каждой точке 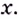 Действительно, приращению
Действительно, приращению 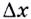 её аргумента
её аргумента 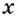 соответствует приращение функции
соответствует приращение функции 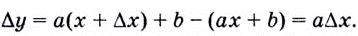 Поэтому
Поэтому 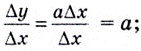 и если
и если  А это и значит, что в каждой точке
А это и значит, что в каждой точке 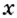 функция
функция 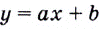 имеет производную
имеет производную 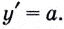
Пишут 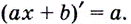
В частности: 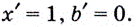
Производная постоянной равна нулю.
Из курса планиметрии известно, что уравнение прямой, проходящей через заданную точку 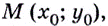 имеет вид
имеет вид 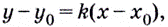 где
где 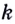 — угловой коэффициент прямой.
— угловой коэффициент прямой.
Поскольку для касательной к графику функции 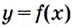 угловой коэффициент равен значению производной в точке касания
угловой коэффициент равен значению производной в точке касания 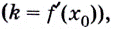 то можем записать общий вид уравнения касательной, проведённой к графику функции
то можем записать общий вид уравнения касательной, проведённой к графику функции 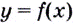 в точке касания
в точке касания 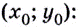
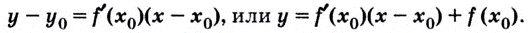
До сих пор речь шла о касательных к криволинейным графикам. Но графиком функции может быть и прямая или часть прямой. Поэтому для обобщения договариваются касательной к прямой в любой её точке считать эту самую прямую. Касательной к отрезку или лучу в любой его внутренней точке считают прямую, которой принадлежит этот отрезок или луч.
Выше было установлено, что производная линейной функции равна коэффициенту при переменной, т.е 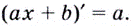
Полученный результат имеет очевидный геометрический смысл: касательная к прямой — графику функции 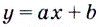 — есть эта самая прямая, её угловой коэффициент равен
— есть эта самая прямая, её угловой коэффициент равен 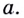
- Заказать решение задач по высшей математике
Пример:
Найдите угол, который образуете положительным направлением оси 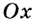 касательная к графику функции
касательная к графику функции 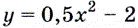 в точке
в точке 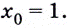
Решение:
Определим сначала угловой коэффициент этой касательной по формуле 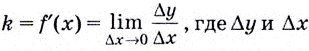 — приращения функции и приращения аргумента соответственно.
— приращения функции и приращения аргумента соответственно.
Найдем приращение функции 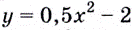 в точке
в точке 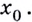
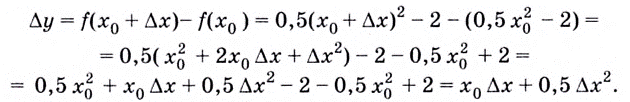
Найдём угловой коэффициент касательной:
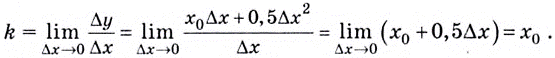
Поскольку 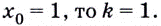
Известно также, что 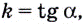 поэтому
поэтому 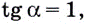 отсюда
отсюда 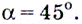
Пример:
Докажите, что для функции 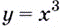 производной есть функция
производной есть функция 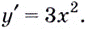
Решение:
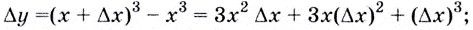
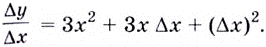 Если
Если 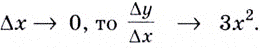 А это и означает, что производной функции
А это и означает, что производной функции 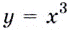 является функция
является функция 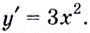
Пример:
Напишите уравнение касательной к графику функции 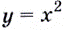 в его точке с абсциссой
в его точке с абсциссой 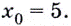
Решение:
Способ 1. Уравнение касательной имеет вид 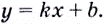 Угловой коэффициент
Угловой коэффициент 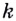 равен значению производной функции
равен значению производной функции 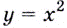 в точке
в точке 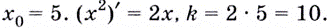 Значит, уравнение касательной
Значит, уравнение касательной 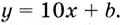 Координаты точки касания
Координаты точки касания 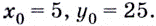 Точка с такими координатами принадлежит касательной, поэтому
Точка с такими координатами принадлежит касательной, поэтому  отсюда
отсюда 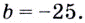 Следовательно, уравнение касательной имеет вид:
Следовательно, уравнение касательной имеет вид: 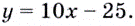
Способ 2. Запишем общий вид уравнения касательной:
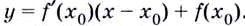
Найдём 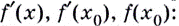
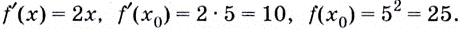
Подставим найденные значения в уравнение касательной:
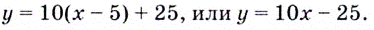
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|