Геометрия метрического пространства

Геометрия метрического пространства

Располагая понятием «расстояние между двумя точками», мы можем определить в произвольных метрических пространствах ряд геометрических понятий.

Определение 1. Замкнутым шаром в метрическом пространстве M называется множество 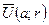точек из M, расстояние от которых до некоторой фиксированной точки 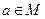не превосходит некоторого числа 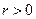: 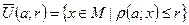. При этом точка a называется центром данного шара, а число r – его радиусом.

Определение 2. Сферой в метрическом пространстве M называется множество 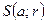точек из M, расстояния от которых до некоторой фиксированной точки 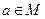равны некоторому числу 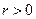: 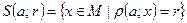. При этом точка a называется центром сферы, а число r – её радиусом.

Примеры: Замкнутый шар в евклидовом пространстве – это обычный шар вместе с ограничивающей его сферой; на евклидовой плоскости – круг вместе со своей границей; на прямой – отрезок.

Сфера в евклидовом пространстве – это обычная сфера, на плоскости – окружность, на прямой – пара точек.

Определение 3. Разность замкнутого шара 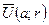и сферы 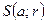называется открытым шаром и обозначается 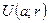. Таким образом, .

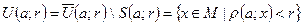Открытый шар 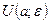называется также 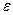– окрестностью точки a.

Свойства окрестностей:

1. Каждая точка a принадлежит всем своим окрестностям.

2. Пересечение любых двух окрестностей точки a содержит окрестность этой точки.

3. Если 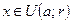, то у точки x есть окрестность, целиком принадлежащая .

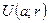4. Любые две различные точки из метрического пространства M имеют непересекающиеся окрестности.