
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задания для подготовки к полугодовой контрольной работе
Задания для подготовки к полугодовой контрольной работе
по алгебре и началам математического анализа
10А класс
1. Решите неравенство:
а) 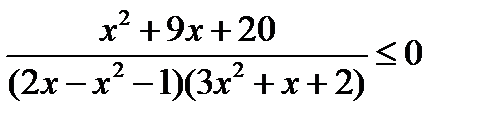 ; б)
; б) 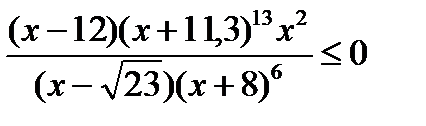 в)
в) 
2. Вычислить: а) 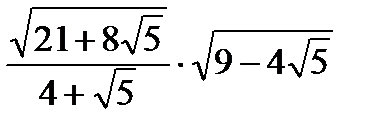 б)
б) 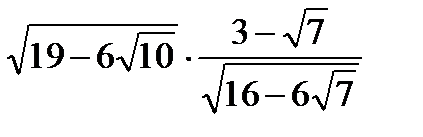
3. Найдите все такие натуральные значения n, при которых выражение 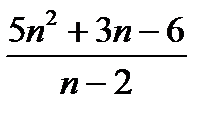 является целым числом.
является целым числом.
4. При каких a и b многочлен 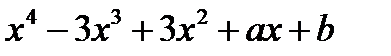 делится на
делится на 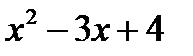 ?
?
5. При каких значениях m и n многочлен 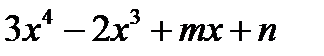 делится без остатка на
делится без остатка на 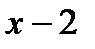 , а при делении на
, а при делении на 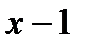 дает остаток равный –14?
дает остаток равный –14?
6. Многочлен Р(х) при делении на х-1 дает в остатке 4, при делении на х-2 дает остаток 8, а при делении на х+1 остаток равен 2. Найдите остаток от деления многочлена Р(х) на 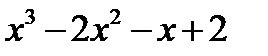 .
.
7. Решите неравенства
а) 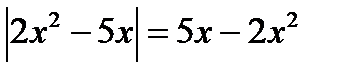 ; б)
; б) 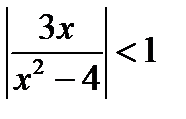 ; в)
; в)  ;
;
г) 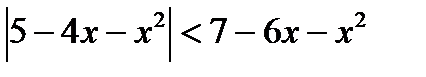 ; д)
; д) 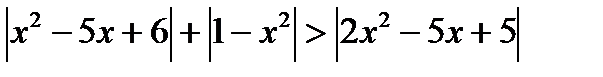
8. Разложите на множители:
а) 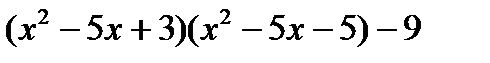 ; б)
; б) 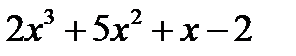 ; в)
; в) 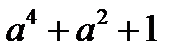 ;
;
г) 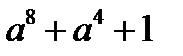 ;д)
;д) 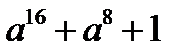 ; е)
; е) 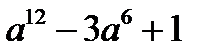
9. Решите однородное уравнение методом введения новой переменной:
а) 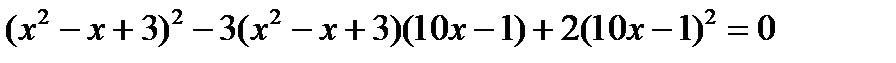 ;
;
б) 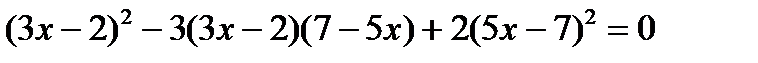
10. Решите уравнения:
а) 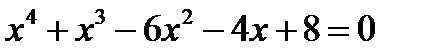 ; б)
; б) 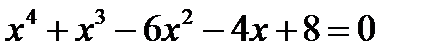 ; в)
; в) 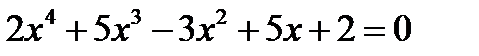 г)
г) 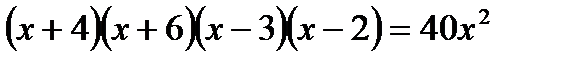
д) 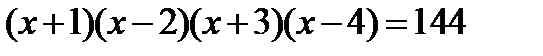 е)
е) 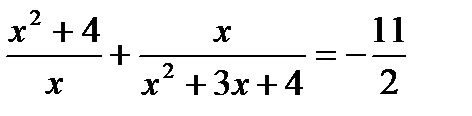
11. Решите уравнение: а) 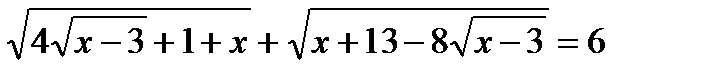 ;
;
б) 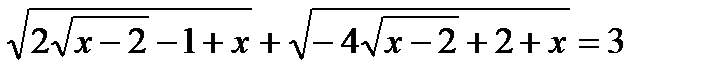
12. Решите уравнение: а) 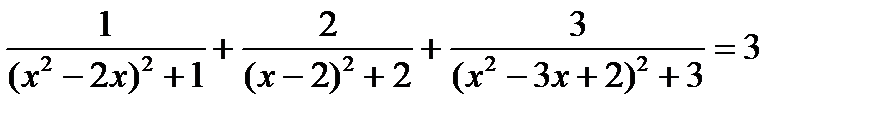
б) 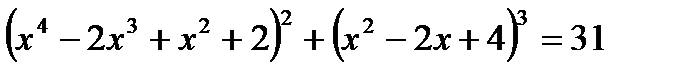
13. Решите уравнения:
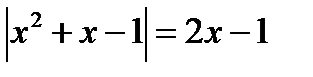
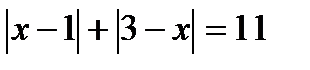
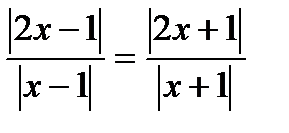
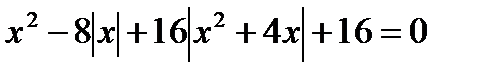
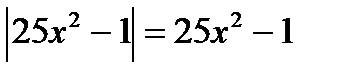
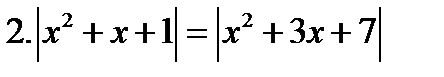
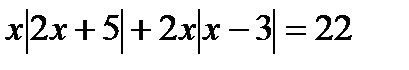
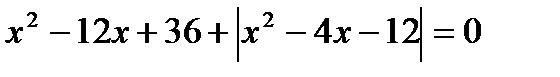
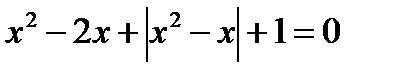
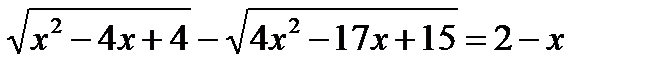
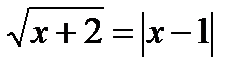
14. Решите неравенства:
а) 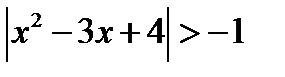 ж)
ж) 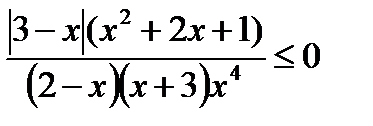
б) 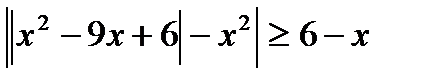 з)
з) 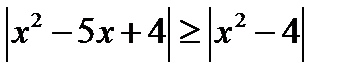
в) 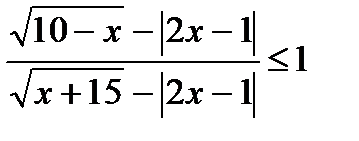 и)
и) 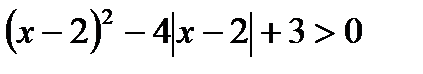
г) 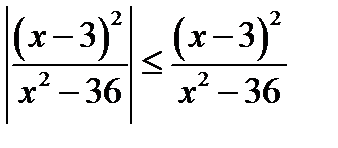 к)
к) 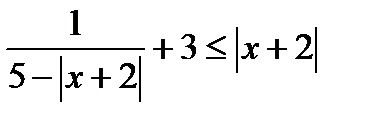
д) 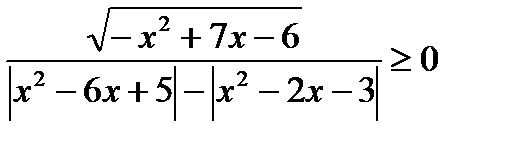 л)
л) 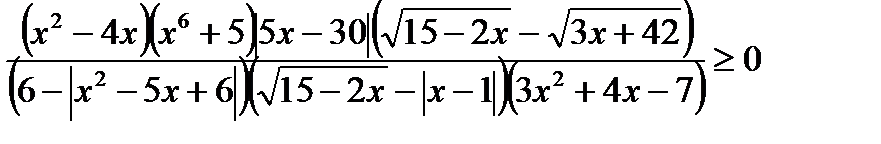
е) 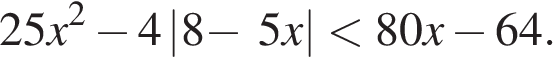 м)
м) 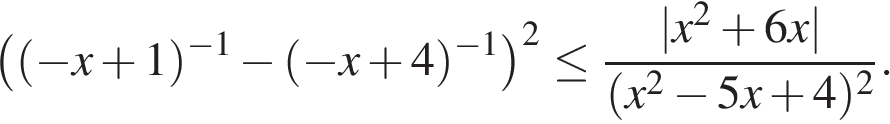
15. Найдите все значения a, при которых уравнение 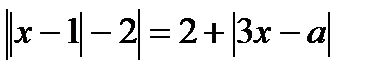 имеет единственное решение
имеет единственное решение
1. Пусть 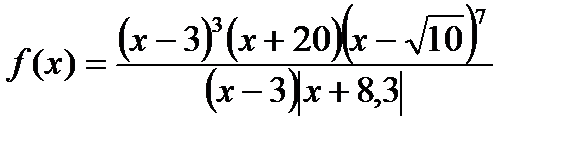
а) Найдите нули функции б) промежутки знакопостоянства в) решите: 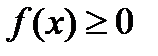
2. Исследуйте функцию на четность
а) 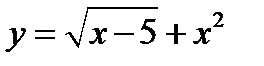 б)
б) 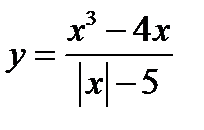
в) 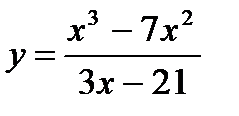 г)
г) 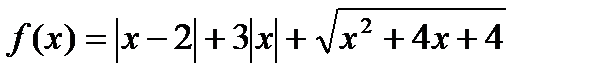
3. Чётная функция y=f(x) и нечетная функция y=g(x) удовлетворяет равенству f(x)+g(x)=x2+3x+2 для всех действительных значений x. Найти f(0,8) и g(-0,6)
4. Чётная функция y=f(x) и нечетная функция y=g(x) удовлетворяет равенству f(x)+g(x)=2x+x2+5для всех действительных значений x. Найти f(-1,8) и g(-0,7)
5. Даны чётная функция y=f(x) и нечетная функция y=g(x). Решите уравнение f(x)=g(x), если для всех действительных значений х выполняется равенство f(x)+g(x)=5x+7
6. Чётная функция y=f(x)обращается в 0 ровно в 17 точках числовой прямой. Найти сумму корней уравнения y=f(10x-3)=0
7. Четная функция 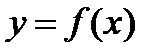 определена на всей числовой прямой. Для всякого неположительного значения переменной x значение
определена на всей числовой прямой. Для всякого неположительного значения переменной x значение 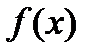 совпадает со значением
совпадает со значением 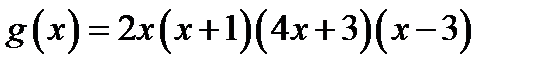 . Сколько корней имеет уравнение
. Сколько корней имеет уравнение 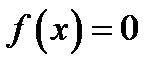 .
.
8. Четная функция 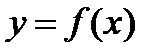 определена на всей числовой прямой. Для всякого неположительного значения переменной x значение
определена на всей числовой прямой. Для всякого неположительного значения переменной x значение 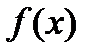 совпадает со значением
совпадает со значением  . Сколько корней имеет уравнение
. Сколько корней имеет уравнение 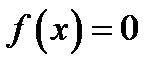 .
.
9. Нечетная функция 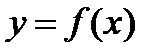 определена на всей числовой прямой. Для всякого неотрицательного значения переменной x значение
определена на всей числовой прямой. Для всякого неотрицательного значения переменной x значение 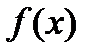 совпадает со значением
совпадает со значением 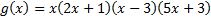 . Сколько корней имеет уравнение
. Сколько корней имеет уравнение 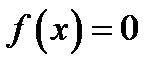 ? Сколько корней имеет уравнение
? Сколько корней имеет уравнение 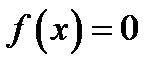 на промежутке (-4; -0,75)?
на промежутке (-4; -0,75)?
10. Функция y=f(x) определена на всей числовой прямой и является нечетной. Для каждого неотрицательного значения аргумента, значение этой функции на 16 меньше, чем значение g(x)=(x2-9x+4)2. Найти число корней уравнения f(x)=0.
11. Найдите значение функции y=3f(-x)-g(-x)f(x) в точке x0≠0, если известно, что функция y=f(x) – четная, y=g(x) –нечетная, f(x0)=1, g(x0)=3
12. Найдите область определения функции
а) 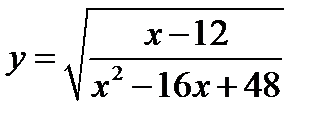
б) 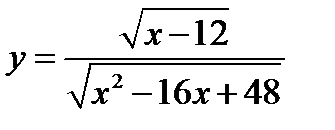
в) 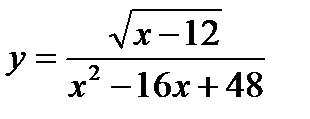
г) 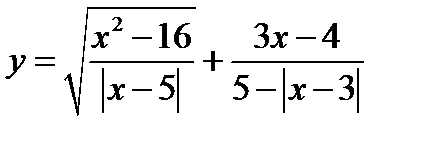
д) f(x)= 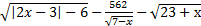
е) 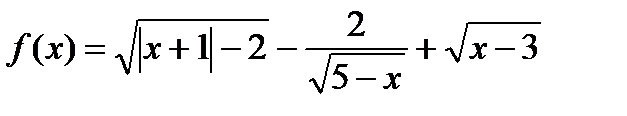
13. Найдите E(y) функции:
а) 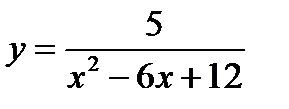 ; б)
; б) 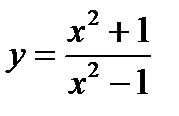 ; в)
; в) 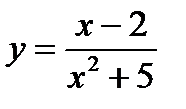 ; г)
; г) 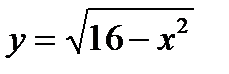 ;
;
д) 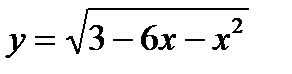 ; е)
; е) 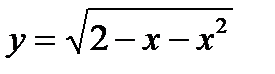 ; ж)
; ж) 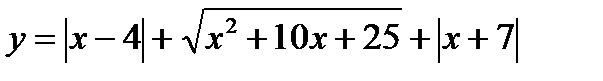
з) 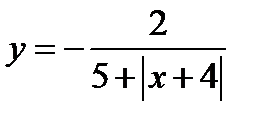 и)
и) 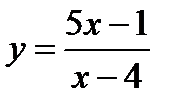 к)
к) 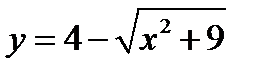 л)
л) 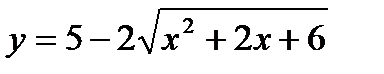
14. а) Найдите наибольшее значение функции 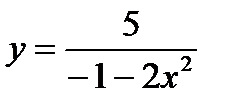 ;
;
б) Найдите наименьшее значение функции 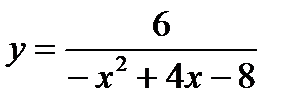
в) Найдите наибольшее и наименьшее значения функции 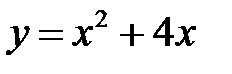 на промежутке
на промежутке 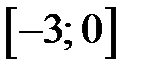
г) Найдите наибольшее и наименьшее значения функции 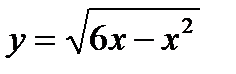 на области определения
на области определения
15. Найдите разность yнаиб – yнаим, если 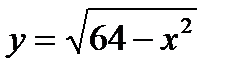 на отрезке
на отрезке 
16. Наибольшее значение функции f(x)=-x2+bx+c равно 11, b в 1,6 раза больше c. Найти отрицательное значение c.
17. Найдите функцию, обратную данной а) 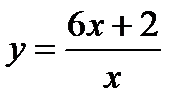 ; б)
; б) 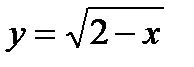 ; в) f(x)=x2+6x+11, x≤3
; в) f(x)=x2+6x+11, x≤3
18. Найдите все значения a, при каждом из которых функция f(x)=x2-2|x-a2|-8x имеет более двух точек экстремума.
19. Решить уравнение 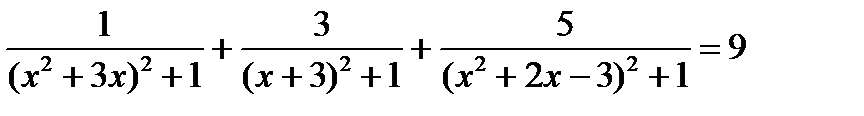
20. Решите уравнения, используя свойства функции:
а) 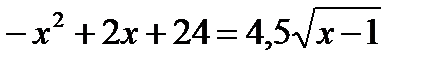 ; б)
; б) 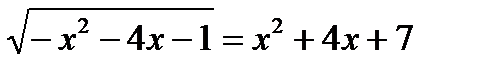 в)
в) 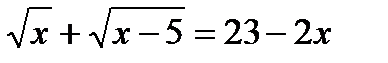 ;
;
г) 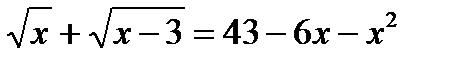 ; д))
; д)) 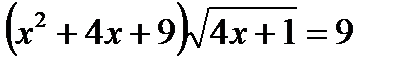 е)
е) 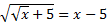
21.  Функция g является обратной к функции
Функция g является обратной к функции 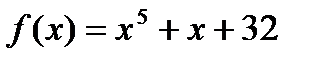 . Решите уравнение
. Решите уравнение 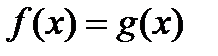
22. Постройте график функции (см. задачи из учебника параграфа 6)
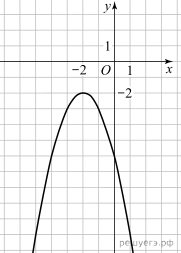
23. На рисунке изображён график функции вида 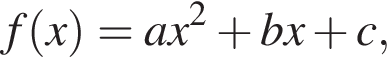 где числа a, b и c — целые. Найдите значение
где числа a, b и c — целые. Найдите значение 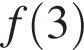 .
.
24.  На рисунке изображён график функции вида
На рисунке изображён график функции вида 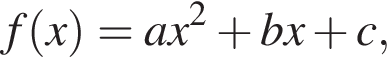 где числа a, b и c — целые. Найдите значение дискриминанта уравнения
где числа a, b и c — целые. Найдите значение дискриминанта уравнения  .
.
25. 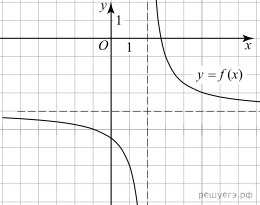 На рисунке изображён график функции вида
На рисунке изображён график функции вида 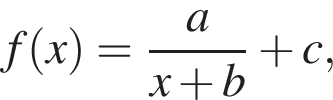 где числа a, b и c — целые. Найдите f (10).
где числа a, b и c — целые. Найдите f (10).
26.  На рисунке изображён график функции вида
На рисунке изображён график функции вида 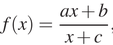 , где числа a, b и c — целые. Найдите a.
, где числа a, b и c — целые. Найдите a.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|