Признак 1. Признак 2. Признак 3

Стр 1 из 2Следующая ⇒

· Урок геометрии. Тема «Свойства параллельных прямых».

· Используя рисунок, выберите верные утверждения:

а) ∠1 и ∠3 – вертикальные;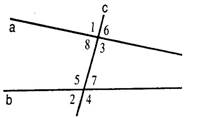

б) ∠5 и ∠1 – односторонние;

в) ∠7 и ∠6 – соответственные;

г) ∠5 и ∠3 – накрест лежащие;

д) ∠2 и ∠4 – смежные;

е) ∠7 и ∠1 – накрест лежащие;

ж) ∠7 и ∠3 – односторонние.

Назовите признаки параллельности прямых.

· Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

· Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

· Если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.

· Из каких частей состоит теорема? (Во всякой теореме различают две части: условие и заключение. Условие – это то, что дано, а заключение – то, что доказывается)

· - что в этих теоремах является условием, а что заключением?

· В этих теоремах условием является первая часть утверждения: «при пересечении двух прямых… углы равны» (это дано), а заключение – вторая часть: «прямые параллельны» (это требуется доказать).

· Итак, сегодня мы, опираясь на знание признаков, попробуем получить свойства параллельных прямых. В каждом признаке выделим условие и заключение;

Признак 1

Признак 2

Признак 3

Условие

При пересечении прямых секущей внутренние накрест лежащие углы равны углов равна 180^о

При пересечении прямых секущей соответственные углы равны

При пересечении прямых секущей сумма односторонних углов равна 180^о

Заключение

Прямые параллельны

Поменяем местами условие и заключение (сформулируйте)

Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.

Закрепление: учебник № 201, №202 стр 65 учебник.

12 Следующая ⇒