Хелпикс

Главная

Контакты

Случайная статья



Глоссарий по теме. Теоретический материал для самостоятельного изучения. Пример 1.. Пример

Стр 1 из 2Следующая ⇒


 

Математика урок 73-74 дата 13.01.22г. группа 3

 Учебник Ш.А Алимов 10-11 Алгебра и начало математического анализа

Тема Производная степенной функции.

Глоссарий по теме

Формула для вычисления производной степенной функции xn, где n – произвольное натуральное число, такова:

(xn) ' =nxn-1

Формула для вычисления производной степенной функции (kx+b)p:

((kx+b)p) ' = pk(kx+b)p

Теоретический материал для самостоятельного изучения

Формула для вычисления производной степенной функции xn, где n – произвольное натуральное число, такова: (xn)’=nxn-1.

Нам уже известна формула производной функции х2: (x2)’=2x.

Пользуясь формулой дифференцирования произведения, получаем:

(x3) ' = (x2·x) ' = (x2) ' · x + x2 · (x) ' = 2x·x+x2·1 = 3x2;

(x4) ' = (x3·x) ' = (x3) '·x+x3·(x) ' = 3x2·x+x3·1 = 4x3.

Заметим, что

(x2) ' = 2x2-1

(x3) ' = 3x3-1

(x4)’=4x4-1

Т.е. для n, равного 2, 3 и 4, формула (1) доказана. Продолжая аналогичные рассуждения, нетрудно убедиться в справедливости формулы (1) для n, равного 5, 6 и т.д.

Пример 1.

Докажем что, 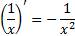, при .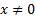

Решение:

1. представим как х-1;

2. воспользуемся формулой (1): (х-1)’=-1·x-1-1=-x-2;

3. вернемся к первоначальному виду

.

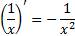В более сложных случаях, например, при нахождении производной функции (3х-1)7, можно воспользоваться следующей формулой:

((kx+b)p)’=pk(kx+b)p-1

Пример

Найдем производную функции (3х-1)7.

Решение:

воспользуемся формулой (2)

((3х-1)7)’=21(3x-1)6.


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.