Определение и примеры метрических пространств

Определение и примеры метрических пространств

Фундаментальными понятиями математического анализа являются понятия предела и непрерывности. В основе этих понятий лежит определение расстояния между двумя точками. Определение расстояния можно распространить на два произвольных элемента некоторого абстрактного множества, сохранив за этим расстоянием основные свойства расстояния между точками прямой, плоскости, пространства.

Определение 1. Пусть M - произвольное множество. Числовую функцию 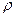, определённую на множестве , называют метрикой на M (а конкретное значение 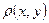- расстоянием от x до y), если при любых x, y, z из M выполняются следующие условия (аксиомы метрики):

1) 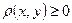; 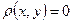тогда и только тогда, когда x=y (аксиома неотрицательности и тождества);

2) 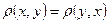(аксиома симметрии);

3) 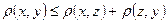(аксиома треугольника).

Определение 2. Множество с введённой на нём метрикой называют метрическим пространством, элементы исходного множества называют при этом элементами или точками пространства.

Примеры метрических пространств:

1. Евклидова прямая. Расстояние между двумя расположенными на ней точками с координатами x и y определяется по формуле

2. Евклидова плоскость. Расстояние между точкам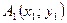и и 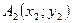вычисляется по формуле

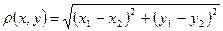3. Евклидово пространство. Расстояние между точкам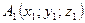и и 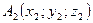вычисляется по формуле

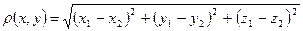4. Метрическое пространство L – множество прямых на плоскости, параллельных прямой y=x, с расстоянием

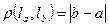где 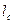– прямая y=x+c.

5. Метрическое пространство N - множество натуральных чисел с расстоянием

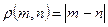Замечание.Каждое метрическое пространство порождает ряд других метрических пространств. Пусть множество 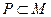, введена метрика 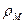, и пусть в P метрика определяется равенством 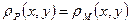, где 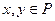. Тогда множество P также является метрическим пространством. Оно называется подпространством пространства M с индуцированной метрикой, заданной в M.