
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 4 . Приведение уравнений динамики одномерных автоматических систем. к стандартному виду
Лекция 4
Приведение уравнений динамики одномерных автоматических систем
к стандартному виду
Отличительным признаком одномерных систем является существование в системе одной выходной (переменная наблюдения 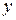 ) и одной входной - управляющего воздействия
) и одной входной - управляющего воздействия 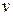 .
.
4.1 Динамика одномерной системы может быть задана следующим описанием:
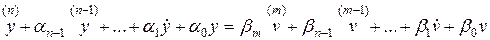 . (4.1)
. (4.1)
Система (4.1) описывается обыкновенным дифференциальным уравнением 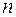 - го порядка с правой частью
- го порядка с правой частью 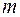 - го порядка, где
- го порядка, где 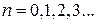 ,
, 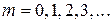 , (при этом:
, (при этом: 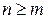 ) и может быть приведена к стандартному виду:
) и может быть приведена к стандартному виду:
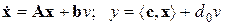 , (4.2)
, (4.2)
где 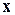 - вектор состояния системы в
- вектор состояния системы в 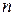 – мерном фазовом пространстве;
– мерном фазовом пространстве; 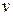 - скалярная переменная (управляющее) воздействие;
- скалярная переменная (управляющее) воздействие; 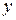 - скалярная переменная (переменная наблюдения);
- скалярная переменная (переменная наблюдения); 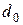 - вещественный коэффициент;
- вещественный коэффициент; 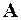 - квадратная (
- квадратная ( 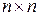 ) действительная матрица состояния;
) действительная матрица состояния; 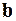 - действительная матрица управления (
- действительная матрица управления ( 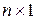 );
); 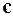 - действительная (
- действительная ( 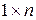 ) матрица наблюдения вида:
) матрица наблюдения вида:
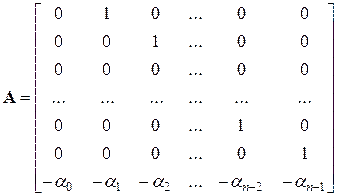 ,
, 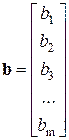 ;
; 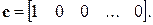 (4.3)
(4.3)
Движения в системе (4.1) возникают как от управляющего воздействия 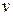 , так и от ненулевых начальных условий (отклонений)
, так и от ненулевых начальных условий (отклонений) 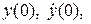
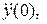
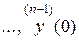 .
.
Система (4.1) всегда полностью наблюдаемая, для полной управляемости должно выполняться условие
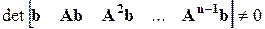 . (4.4)
. (4.4)
В описании (4.2) составляющие 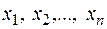 вектора
вектора 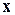 определяются в соответствии со следующими выражениями
определяются в соответствии со следующими выражениями
а) при 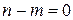 (представлено на рисунке 4.1):
(представлено на рисунке 4.1):
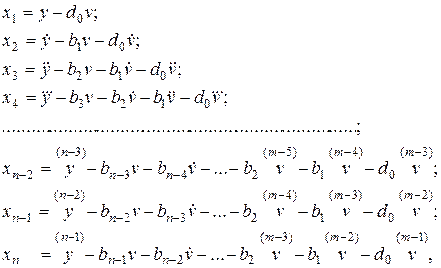 (4.5)
(4.5)
б) при 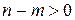 (представлено на рисунках 4.2 - 4.5):
(представлено на рисунках 4.2 - 4.5):
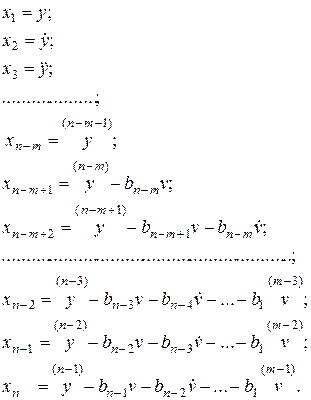 (4.6)
(4.6)
Коэффициенты 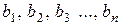 в (4.3) и
в (4.3) и 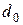 в (4.2) определяются через коэффициенты
в (4.2) определяются через коэффициенты 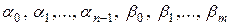 согласно выражениям:
согласно выражениям:
а) при 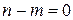
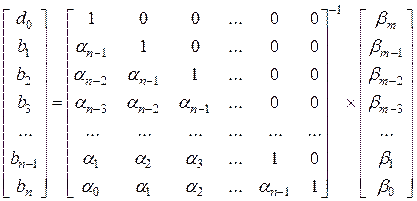 ; (4.7)
; (4.7)
б) при 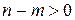
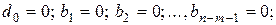
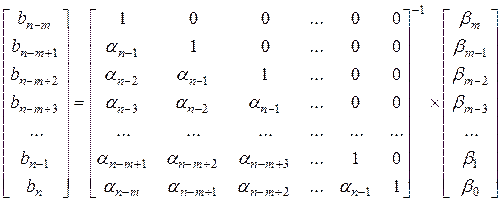 . (4.8)
. (4.8)
В структурном виде система (4.1), преобразованная к стандартному виду (4.2) - (4.3) при 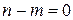 представлена на рисунке 4.1, при
представлена на рисунке 4.1, при 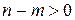 и
и 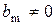 – на рисунках 4.2 - 4.4.
– на рисунках 4.2 - 4.4.
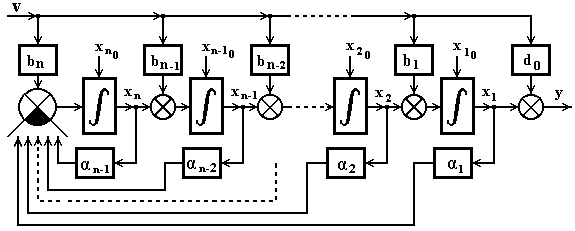
Рисунок 4.1 – Структура преобразованной системы при 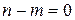
В структурном виде система (4.1), преобразованная к стандартному виду (4.2) - (4.3) при 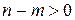 и
и 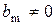 – на рисунках 4.2 - 4.4.
– на рисунках 4.2 - 4.4.
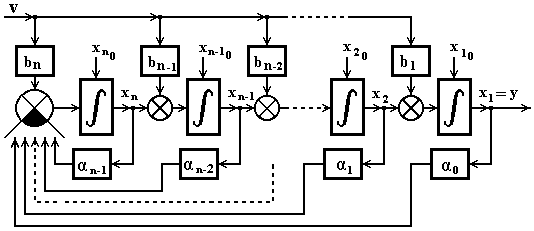
Рисунок 4.2 – Структура преобразованной системы при 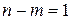
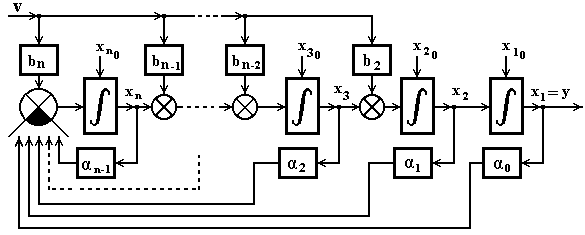
Рисунок 4.3 – Структура преобразованной системы при 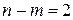
Аналогично можно получать структурные схемы при 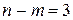 ,
, 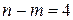 , … и т.д. вплоть до
, … и т.д. вплоть до 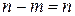 (
( 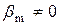 ) (представлено на рисунке 4.4).
) (представлено на рисунке 4.4).
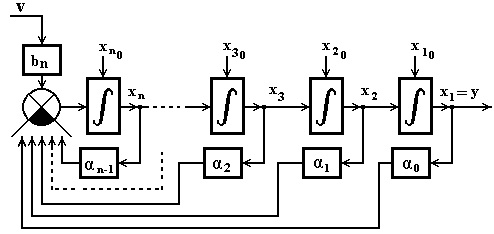
Рисунок 4.4 – Структура преобразованной системы при 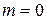 и
и 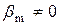
В структурном виде система (4.1), преобразованная к стандартному виду (4.2) - (4.3) при 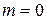 и
и 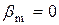 представлена на рисунке 4.5. В системе (4.1) при этом будет отсутствовать правая часть (система становится однородной). Движения в такой системе возникают только от ненулевых значений начальных условий (начальных отклонений)
представлена на рисунке 4.5. В системе (4.1) при этом будет отсутствовать правая часть (система становится однородной). Движения в такой системе возникают только от ненулевых значений начальных условий (начальных отклонений) 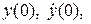
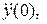
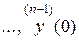 .
.
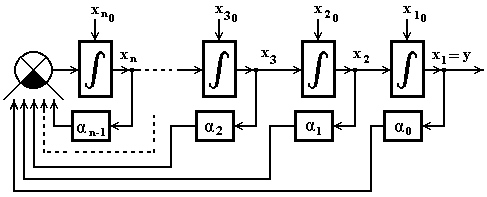
Рисунок 4.5 – Структура преобразованной системы при 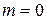 и
и 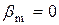
Система (4.1) всегда полностью наблюдаема по выходу (переменная 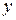 ), при
), при 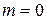 и
и 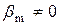 (представлено на рисунке 4.4) всегда полностью управляема, при
(представлено на рисунке 4.4) всегда полностью управляема, при 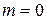 и
и 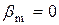 (представлено на рисунке 4.5) понятие управляемости неприменимо.
(представлено на рисунке 4.5) понятие управляемости неприменимо.
Пример 4.1. Пусть система (4.1) при 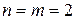 имеет следующий вид
имеет следующий вид
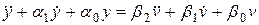 . (4.9)
. (4.9)
Система (4.9) может быть приведена к частному случаю системы (4.2) вида
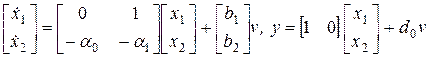 . (4.10)
. (4.10)
В описании (4.10) переменные состояния 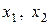 связаны с переменными состояния
связаны с переменными состояния 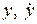 и переменными
и переменными 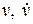 в описании (4.9) в соответствии с (4.5) следующими уравнениями:
в описании (4.9) в соответствии с (4.5) следующими уравнениями:
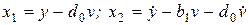 ,
,
где, в соответствии с (4.7)  ,
, 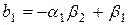 ,
,  .
.
В структурном виде система (4.10) представлена на рисунке 4.6.
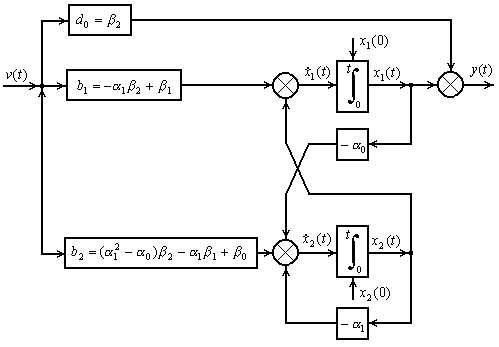
Рисунок 4.6 - Структурная математическая модель системы 4.10
Система по выходному сигналу 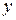 всегда полностью наблюдаема, условие полной управляемости по входному управляющему сигналу
всегда полностью наблюдаема, условие полной управляемости по входному управляющему сигналу 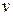 определяется по -
определяется по - 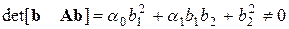 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|