Методы вычисления интеграла Римана

3. Вычислить длину дуги кривой 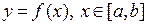.Длиной дуги кривой мы будем называть предельную сумму длин вписанных в дугу хорд при стремлении этих хорд к точкам.

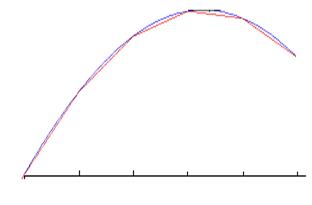
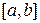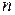Разобъем отрезок на отрезков 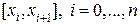, где 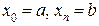. Длина хорды, расположенной над отрезком 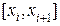, равна 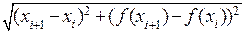. Воспользуемся формулой конечных приращений Лагранжа и получим длину этой же хорды в ви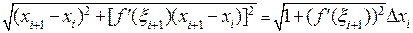де

, где ,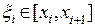

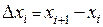. Таким образом, длина дуги всей кривой может быть приближена суммой 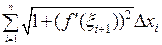, причем чем мельче разбиение отрезка 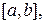тем точнее результат. При стремлении длины наименьшего из отрезков разбиения к нулю мы получим из суммы интеграл: 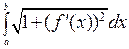, который и дает выражение длины дуги данной кривой.

В случае, когда кривая задана параметрически: 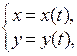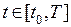, длина дуги этой кривой вычисляется по формуле .

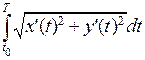4. Вычислить объем тела вращения, ограниченного поверхностью вращения кривой 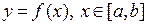, вокруг оси OX и плоскостям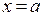и и .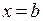

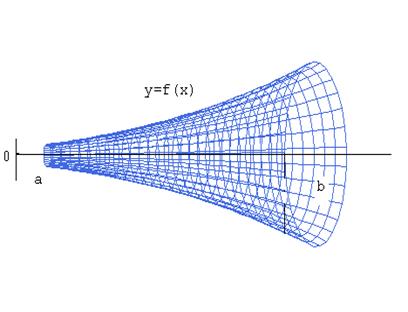
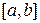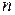Разбивая отрезок на отрезков 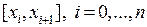, где 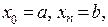и проводя плоскости 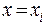, мы разобъем тело вращения на пласты, расположенные над отрезками 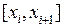. Если высота пласта (длина отрезка 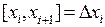) небольшая, его объем можно приблизить объемом цилиндра, радиуса 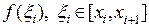, боковая поверхность которого расположена над тем же отрезком 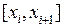. При этом объемы цилиндра и пласта тем ближе, чем меньше величина 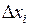. Объем такого цилиндра равен 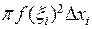. Поэтому приближенное значение объема заданного тела вращения равно

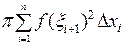. Переходя к пределу в такой интегральной сумме, получим .

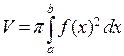Методы вычисления интеграла Римана

Благодаря формуле Ньютона-Лейбница вычисление интеграла сводится к отысканию первообразной и вычислению значений этой первообразной в концах отрезка интегрирования. Поэтому основные приемы вычисления интеграла Римана так же, как в случае неопределенного интеграла, – замена переменной и интегрирование по частям.

1. Замена переменной. Пусть 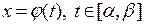, где 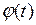– монотонная непрерывная функция, имеющая непрерывную производную на интервале 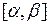, причем 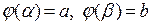. Тогда .

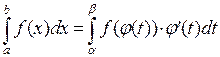Доказательство. Пусть 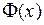– первообразная для 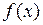. Тогда 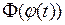– первообразная для 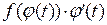. Согласно условию .

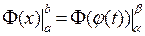П р и м е р. Вычислить 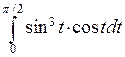. Сделаем замену 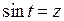. Монотонная на отрезке функция 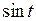отображает этот отрезок в отрезок 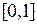. Поэтому .

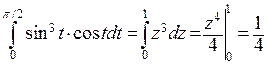2. Интегрирование по частям. Справедлива следующая формула: .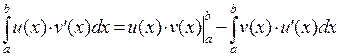

Доказательство. Так как согласно формуле Ньютона-Лейбница 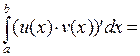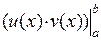и согласно свойству определенного интеграла 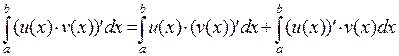, сравнивая правые части последних двух равенств, получим требуемую формулу.

П р и м е р. .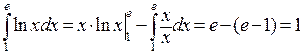

При вычислении интегралов Римана можно использовать пакет программ MAXIMA. Для получения 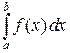необходимо ввести команду integrate(f(x),x,a,b) и нажать Shift+Enter.