Контакты

Случайная статья

Замена переменной в интеграле.

2. Замена переменной в интеграле.

Докажем, что если 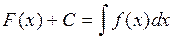, то .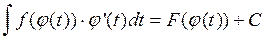

Доказательство. Имеем: 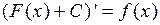. Следовательно, согласно правилу дифференцирования сложной функции

.

Формулу интегрирования заменой переменной можно записать в виде

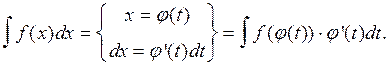
После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования 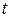назад к старой переменной .

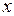При подходящей замене переменной мы сводим заданный интеграл к табличному.

П р и м е р 1.Найти 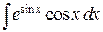. Здесь 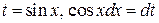. Следовательно, в соответствии с тем, что 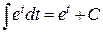, имеем .

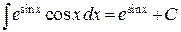П р и м е р 2.Найти 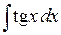. Сделаем замену 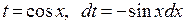. Тогда .

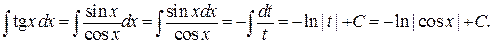П р и м е р 3.Найти 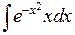. Сделаем замену 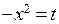. Тогда 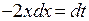и

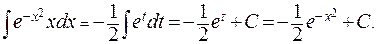
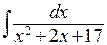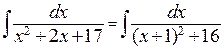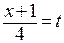П р и м е р 4. Найти . Выделим полный квадрат в знаменателе: . Вынесем 16 из знаменателя: и сделаем замену . Теперь мы получили табличный интеграл: 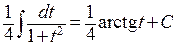. В результате имеем .

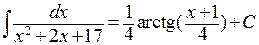3. Интегрирование по частям.

Пусть 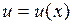, 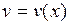– функции, имеющие непрерывные производные. Тогда

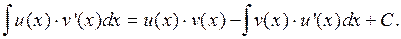
(или ).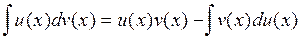

Доказательство. Справедливы соотношения:

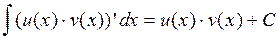и

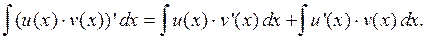
Сравнивая правые части, получим приведенную выше формулу.

П р и м е р 1.Найти 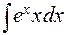. Обозначим 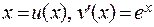. Тогда 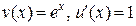. Применяя формулу интегрирования по частям, получим

.

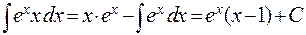П р и м е р 2. Найти 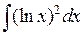. В этом примере мы применим метод

интегрирования по частям дважды:

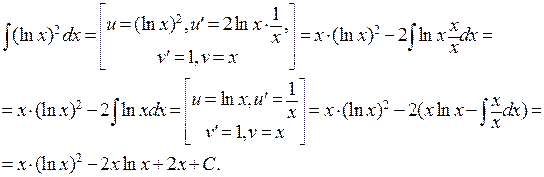
Домашнее задание: Минорский, 1317-1328, 1375-1382.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.