
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конспект лекции. Основные методы вычисления неопределенного интеграла. Интегрирование выражений, содержащий квадратный трехчлен ax2+bx+c
Конспект лекции
Основные методы вычисления неопределенного интеграла
Интегрирование выражений, содержащий квадратный трехчлен ax2+bx+c
Рассм. некоторые виды интегралов, содержащих квадратный трехчлен в подынтегральном выражении, и способы их вычисления. Всюду далее считаем a, b, c≠0.
1) Интеграл вида 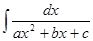
Выделим полный квадрат в квадратном трехчлене: 
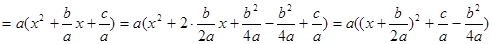
Сделаем замену переменной 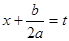 . Тогда интеграл в зависимости от знака выражения
. Тогда интеграл в зависимости от знака выражения 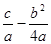 , сводится к одному из интегралов:
, сводится к одному из интегралов: 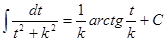 или
или 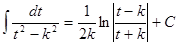
Замечание: вместо замены переменной (после выделения полного квадрата) можно использовать также метод поднесения под знак дифференциала.
Пример_1. Найти неопределенный интеграл: а) 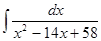 ; б)
; б) 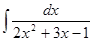 .
.
а) 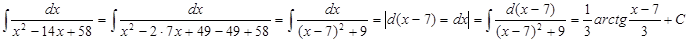
б) 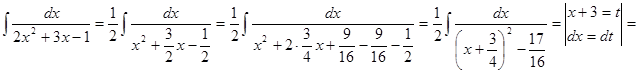
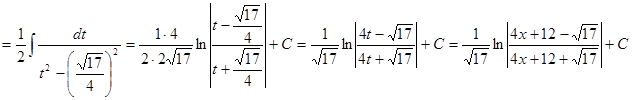
2) Интеграл вида 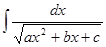
Также вычисляется выделением полного квадрата в квадратном трехчлене. Он сводится к интегралу: 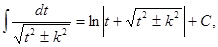 если а>0 или
если а>0 или  если a<0.
если a<0.
Пример_2. Найти неопределенный интеграл: а) 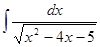 ; б)
; б) 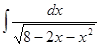 .
.
а) 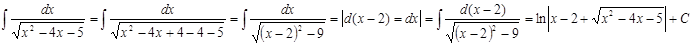
б) 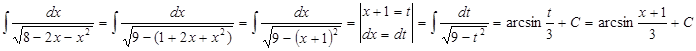
3) Интеграл вида 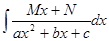 , где M≠0.
, где M≠0.
В числителе подынтегральной функции выделяем производную 2ax+b квадратного трехчлена, записанного в знаменателе. Тогда интеграл можно представить в виде суммы двух интегралов, один из которых сводится к интегралу 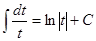 , а второй вычисляется как интеграл вида
, а второй вычисляется как интеграл вида 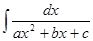 .
.
Пример_3. Найти неопределенный интеграл: 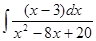 .
.
Найдем производную квадратного трехчлена, записанного в знаменателе дроби: 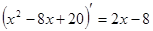 . Выделим производную знаменателя в числителе дроби:
. Выделим производную знаменателя в числителе дроби:
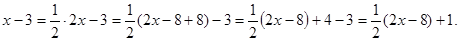
Тогда 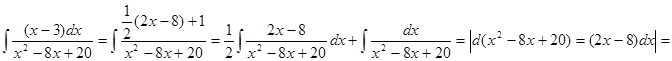
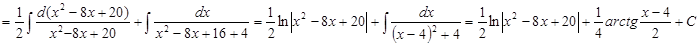
4)Интеграл вида 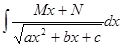 , где М≠0 сводится к сумме интегралов
, где М≠0 сводится к сумме интегралов 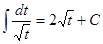 и вида
и вида 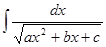 .
.
Пример_4. Найти неопределенный интеграл:  .
.
Выдели в подкоренном выражении полный квадрат: 4x-x2=-(x2-4x+4-4)=-(x-2)2+4
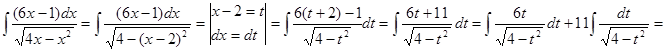
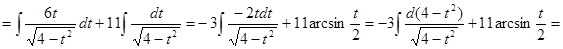
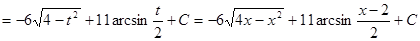
5)Интегралы вида 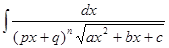 (n=1,2) сводятся к рассмотренным выше интегралам при помощи подстановки
(n=1,2) сводятся к рассмотренным выше интегралам при помощи подстановки 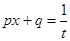 .
.
Пример_5. Найти неопределенный интеграл: 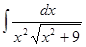 .
.
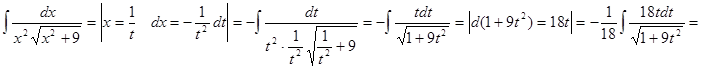
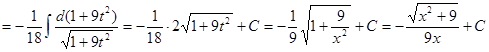
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|