КОНСПЕКТ. з методів обчислень. підготувала студентка групи 31 фмі. Соловій Надія. Конспект 1. Правило Рунге для подвійного перерахунку похибок. Конспект 2. Інтерполяційний многочлен Ерміта. Конспект 3. Обчислення визначених інтегралів метода ми Монте-Карл

Конспект 2. Інтерполяційний многочлен Ерміта.

Конспект 3. Обчислення визначених інтегралів методами Монте-Карло.

Метод чисельного інтегрування Монте–Карло – це найбільш відоме застосування статичного моделювання для розв’язання прикладних математичних задач. Якщо з послідовністю випадкових чисел 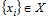 з законом розподілу ймовірностей 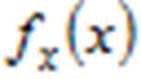провести функціональне перетворення  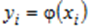то математичне очікування отриманої послідовності випадкових чисел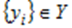  

(6.32)

при обсязі вибірки більше декількох тисяч чисел з достатньо високою точністю може бути оцінено за формулою 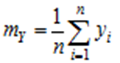 (6.33)

Введемо в вирази (6.29), (6.30) так звану функцію індикатора області

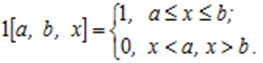
Якщо тепер обрати функцію 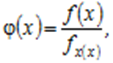 то кінцевий вираз буде мати вигляд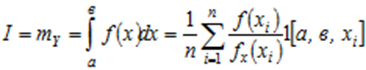  

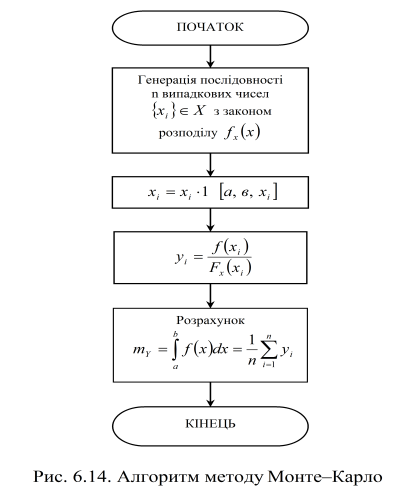
Алгоритм обчислення визначеного інтегралу за методом Монте–Карло наведено на рисунку 6.16.

Похибка методу Монте–Карло визначається похибкою генерації псевдовипадкової послідовності чисел, що згенеровані на ЕОМ, та обсягом вибірки. Вона може бути оцінена із співвідношення 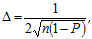 (6.34)

де Р – гарантована ймовірність влучання похибки в інтервал  ;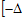

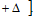Кількість випробувань n не залежить від кратності інтегралу, тому метод Монте–Карло знаходить застосування для обчислення багатократних інтегралів, де застосовувати інші методи чисельного інтегрування неефективно через сильне збільшення кількості обчислювальних операцій.

Розглянемо послідовність дій при обчисленні кратних інтегралів. Для реалізації цієї процедури перш за все потрібно мати m генераторів випадкових чисел, де m – дорівнює кратності інтегрованих.

Геометрично, обчислення m – кратного інтегралу 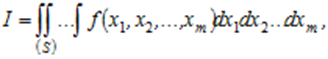(6.35)

де 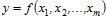  – неперервна функція в обмеженій замкненій області S, зводиться до визначення  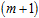 – вимірного обсягу прямого циліндра в просторі  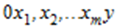, що побудований на основі S й обмежений зверху поверхнею  .

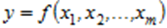Для перетворення інтегралу (6.20) таким чином, щоб нова область інтегрування цілком знаходилась в середині одиничного m – вимірного куба , зробимо заміну змінних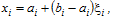

де 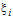 – відповідні координати від 0 до 1;  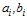– граничні значення координат, де розташована область інтегрування.

Тоді з (6.35) отримуємо 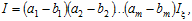 де

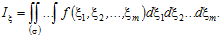
Якщо застосувати m генераторів рівномірно розподілених випадкових чисел в діапазоні (0,1), то обчислення середнього значення функції від їх комбінацій з застосуванням багатовимірного індикатора області інтегрування дасть шукану оцінку інтегралу

,

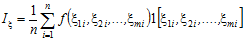де 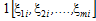  дорівнює 1, якщо точка потрапляє в середину області інтегрування, і 0, якщо не потрапляє.

Похибка обчислення m-кратного інтегралу за методом Монте–Карло оцінюється аналогічно однократному за формулою (6.34).