
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 6. Производная функции.
Лекция 6. Производная функции.
6.1. Производная функции, ее геометрический и физический смысл.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
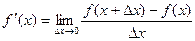
 у
у
f(x)
f(x0 +Dx) P
Df
f(x0) M
a b Dx
0 x0 x0 + Dx x
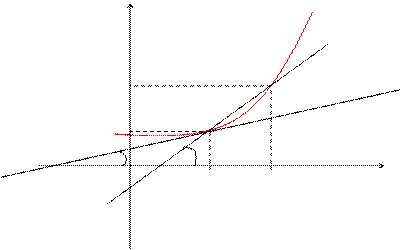
Пусть f(x) определена на некотором промежутке (a, b). Тогда 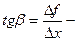 тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.
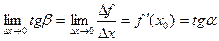 ,
,
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой: 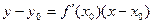
Уравнение нормали к кривой: 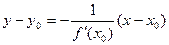 .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
6.2. Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения 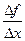 при условии, что это отношение существует.
при условии, что это отношение существует.
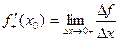
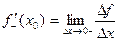
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
6.3. Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3) 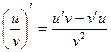 , если v ¹ 0
, если v ¹ 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
6.4. Производные основных элементарных функций.
1)С¢ = 0; 9) 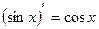
2)(xm)¢ = mxm-1; 10) 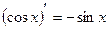
3) 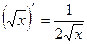 11)
11) 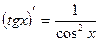
4) 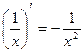 12)
12) 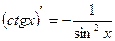
5) 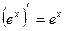 13)
13) 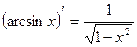
6) 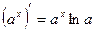 14)
14) 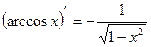
7) 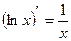 15)
15) 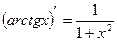
8) 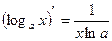 16)
16) 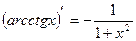
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|