ЛЕКЦИЯ 4.. Энтропия и направленность эволюционных процессов.. Бифуркации.

ЛЕКЦИЯ 4.

Энтропия и направленность эволюционных процессов.

Бифуркации.

Если мы закроем дверь перед заблуждением, то, как же тогда войдет Истина.

Рабиндранат Тагор

1. ДЕЙСТВИЕ И ПРОТИВОДЕЙСТВИЕ В ПРИРОДЕ. ОТ ЗАКОНОВ ФИЛОСОФИИ К ПРИНЦИПУ ЛЕ ШАТЕЛЬЕ-БРАУНА

При анализе направленности эволюционных процессов обычно исходят из второго начала термодинамики, выраженного через энтропию S, которую представляют как меру хаоса в системе. Увеличение энтропии (AS > 0) соответствует увеличению степени хаоса в системе, и наоборот, упорядочение системы должно сопровождаться уменьшением энтропии (AS < 0).

Согласно второму началу термодинамики в формулировке Клаузиуса, в любой изолированной системе (не обменивающейся энергией, в том числе тепловой, с окружающим пространством) энтропия — функция неубывающая (AS > 0). Поэтому в рамках термодинамики обычно делается вывод (назовем такой подход классическим).

Эволюция любой изолированной (предоставленной самой себе) системы, всегда идет в направлении от порядка к хаосу (dS ≥0).

Чтобы лучше представить себе физику дела, напомним формулировку второго начала термодинамики, выражающую известный термодинамический принцип — невозможна самопроизвольная передача тепла от менее нагретого тела к более нагретому, математическая запись которого, предложенная Клаузиусом, выглядит следующим образом: dS ≥ bQ/T.

Здесь Q — тепловая энергия, Т — температура, δ — означает неполный дифференциал (приращение),
S = -k_Бlnw— энтропия по Больцману, k_Б— постоянная Больцмана, w — вероятность нахождения системы в данном макроскопическом состоянии (макросостояние). При δQ = 0 (изолированная система) последнее выражение сводится к написанному выше: ΔS ≥ 0, или в дифференциальной форме — dS ≥ 0.

Поясним физический смысл понятия энтропии по Больцману на классическом для теории вероятностей примере бросания монет. Есть два варианта исхода падения монеты после бросания — условно орел или решка. С позиций математики это означает, что вероятность реализации каждого состояния р = 1/2. Однако всегда надо помнить, что эта вероятность реализуется тем лучше, чем больше число бросаний или число одновременно бросаемых монет, т. е. о вероятностном исходе можно говорить, только если число событий существенно превышает величину 1/р. Только подбросив монету 100 раз или более, можно ожидать, что примерно в половине случаев (т. е. в 50 из 100 бросаний) она упадет орлом, а в оставшейся половине — решкой.

Выше мы реализовали статистическую ситуацию, называемую в физике усреднением по времени. Но можно поступить иначе. Возьмем 100 одинаковых монет (или, как говорят в физике, — ансамбль монет) и подбросим их одновременно. Каждая из монет ансамбля, независимо от других, может упасть орлом или решкой. Положение монет, которое реализуется после их падения, называется данным реализованным макроскопическим состоянием. Подсчитаем количество монет в этом реализованном макроскопическом состоянии, которые легли орлом и решкой. Если среди монет нет дефектных, можно ожидать, что примерно половина их ляжет орлом, половина — решкой. Подбросим монеты еще раз и реализуем следующее макроскопическое состояние. Снова подсчитаем количество монет, которые легли орлом и решкой. Так поступим много раз, выполнив, например, 1000 или больше бросаний. Можно ожидать, что не всегда количество монет, выпавших орлом и решкой, будет совпадать.

Построим график, на котором по горизонтали отложим количество монет из 100 бросаемых, выпавших орлом (решкой), по вертикали — количество макроскопических состояний, соответствующих таким реализациям. Обычно получается график типа представленного на рисунке 2.18. Чаще всего реализуются макроскопические состояния, для которых количество монет, выпавших орлом и решкой, примерно одинаково. Наименьшее число реализаций будет соответствовать случаям выпадения большинства монет орлом или решкой. Если поделить количество выпадений того или иного числа монет орлом или решкой на полное количество бросаний (т. е. произвести нормировку), мы получим ранее введенную величину w. Очевидно также, что выпадение всех монет орлом или решкой соответствует полностью упорядоченному их состоянию (аналогично вещам, аккуратно разложенным на полках шкафа), в то время как случайное их расположение — хаосу. Поскольку последнему состоянию соответствует максимальное значение w, соответствующая ему энтропия — максимальна, в то время как полному упорядочению соответствует минимальное значение энтропии.

Существование среди множества разнообразных систем в природе сложных неравновесных макроскопических систем, в которых «порядок рождается из хаоса», стимулировало ряд работ, в которых были заложены основы теории самоорганизации. Все развитые подходы ориентируются на приведенное выше выражение для второго начала термодинамики, и поэтому в качестве обязательного условия существования явления самоорганизации требуют, чтобы система была открытой, т. е. обменивалась с окружающей средой хотя бы энергией (в общем случае также энтропией, веществом и излучением).

Это, в свою очередь, означает, что уменьшение энтропии системы, в которой происходят процессы самоорганизации, должно сопровождаться обязательным увеличением суммарной энтропии («система» + «окружающая среда»).

Но если процессы самоорганизации на Земле еще можно пытаться объяснить (с весьма большими натяжками) увеличением степени хаоса в окружающем пространстве, то для объяснения эволюции Вселенной в целом,^{^[1]} теория самоорганизации в приводимой выше трактовке вынуждена умалчивать либо о необходимости некоторого «параллельного» мира (помимо нашей метагалактики), до сих пор никем не обнаруженного, за счет которого наблюдаются процессы упорядочения в нашей метагалактике, либо признать идею божественного создания мира.

В классическом подходе к процессам самоорганизации существуют и другие, скрытые, противоречия.

Во-первых, такой подход нарушает принцип дополнительности, в соответствии с которым всегда требуется рассматривать пары взаимодополняющих параметров, описывающих любую систему.

Во-вторых, нарушается фундаментальный закон природы, суть которого в философии отражают законы единства и борьбы противоположностей и отрицания отрицаний, эквивалентом которым в точных науках являются в механике — третий закон Ньютона, в электродинамике — правило Ленца и закон электромагнитной индукции Фарадея, а в обобщенном виде — принцип Ле Шателье-Брауна, утверждающие каждый в своей основе, что любое действие порождает противодействие (рис. 2.19).

Это означает, что если рассматривается энтропийный механизм перехода от хаоса к порядку или наоборот, то должен быть включен в рассмотрение и какой-то другой механизм противодействия ему.

В-третьих, возникает весьма существенная проблема для объяснения процессов самоорганизации на Земле. Многолетние измерения потоков радиации с помощью приборов, установленных на спутниках, показали, что интегральный энергетический баланс Земли в среднем за год равен нулю. Таким образом, количество тепловой энергии, получаемое Землей от Солнца в точности равно энергии, излученной Землей в космическое пространство. Поэтому оказывается непонятным, за счет какой энергии развивается (усложняется) жизнь на Земле?

Попытка обойти это обстоятельство привела к введению в рассмотрение нового процесса, который называется «получение информации» и в большинстве работ связывается с понятием «отрицательной энтропии» («негаэнтропии»), предложенной Шредингером. При этом молчаливо предполагается, что количество «информации», получаемой Землей из космического пространства и определяющей сложность системы с точки зрения упорядочения, равно притоку негаэнтропии к системе. Такой подход формально имеет право на существование, но дает мало принципиально нового в смысле понимания физики механизма самоорганизации.

Однако оказывается, что в термодинамике, как науке о тепловых явлениях, давно уже есть правила, определяющие направления таких процессов через понятия термодинамических потенциалов:

Для любой термодинамической системы, в которой нельзя пренебречь энергией взаимодействия между ее элементами, существует критическое значение ее энергии, характеризуемое обычно так называемой температурой термодинамического равновесия Ткр, выше которого система, предоставленная самой себе, будет эволюционировать в направлении увеличения степени хаотичности, а ниже — к усложнению через упорядочение.

Если взаимодействие между объектами системы отсутствует (например, идеальный газ), имеется только один сценарий развития — от порядка к хаосу.

Поясним это утверждение. Запишем первое начало термодинамики через величину dU изменения внутренней энергии U системы (которая по определению есть сумма кинетических энергий хаотического движения, т. е. тепловой энергии, вращательного и колебательного движений молекул вещества и потенциальной энергии их взаимодействия) и совершенную работу δА:δQ= dU + δА.

Изменение внутренней энергии dU включает минимум две макросоставляющие (dU=dU₁+ dU₂), определяющие ее изменение за счет изменения температуры на величину dT при нагревании — dU₁= cm dT (с — удельная теплоемкость системы, т — масса) и при фазовом превращении — dU₂ = ±λdm (λ — удельная теплота фазового превращения, например плавления, кристаллизации или конденсации, dm — масса вещества, изменившего агрегатное состояние).

Увеличению степени упорядочения некоторой массы вещества системы dm (т. е. уменьшению энтропии) при неизменной температуре, как правило, соответствует понижение внутренней энергии за счет составляющей dU₂ (dU₂ < 0).

Вспомним известный факт. Лед и вода представляют собой упорядоченный в виде кристаллической структуры и хаотический набор одних и тех же молекул. Известно, что они могут достаточно долго сосуществовать вместе при температуре 0°С. Однако, чтобы разупорядочить часть молекул (превратить часть льда в воду) без изменения температуры требуется подвести к системе «вода — лед» определенное количество теплоты, т. е. увеличить внутреннюю энергию молекул льда. И наоборот, чтобы упорядочить часть молекул воды (превратить воду в лед), необходимо «отобрать» у этих молекул часть внутренней энергии. Таким образом, при одинаковой температуре упорядоченному расположению молекул в кристаллах льда соответствует меньшее значение той части внутренней энергии, которая отвечает за взаимодействие молекул. Следовательно, упорядочение атомов (образование кристаллической структуры), как правило, сопровождается понижением внутренней энергии, стремление к хаосу — повышением.

Второе начало термодинамики можно переписать в виде TdS ≥ δQ, или, с учетом первого начала, TdS >dU + δА.

Отсюда следует, что упорядочение (понижение энтропии, dS < 0) может осуществляться за счет совершения работы внешних сил (δА < 0) над системой (удерживая, например, в вертикальном положении карандаши, рассыпанные по поверхности стола), за счет уменьшения внутренней энергии, т. е. dU < 0 (понижение температуры или фазовое превращение, например кристаллизация жидкости), или за счет обоих механизмов одновременно.

Первый случай с точки зрения самоорганизации не представляет особого интереса. Поэтому проанализируем только второй механизм.

Рассмотрим термодинамическую систему, т. е. систему, состоящую из достаточно большого числа объектов (молекул), взаимодействующих между собой. Как в механике, любое тело, предоставленное самому себе, стремится занять положение, соответствующее возможно минимальному для ситуации значению потенциальной энергии (не удерживаемое ничем тело будет падать или соскальзывать вниз по наклонной плоскости до тех пор, пока не встретит препятствие), так и любая термодинамическая система, предоставленная самой себе, стремится к состоянию с минимально возможным значением характеристики, которая в термодинамике называется свободной энергией Т, и определяется выражением F=U - TS.

Исходя из определения свободной энергии, ее изменение dT можно записать в виде dF=dU-TdS-SdT.

Из этого соотношения следует, что для процессов с квазистационарной или слабо изменяющейся температурой (dT ≈ 0) имеется, по крайней мере, два способа уменьшения значения свободной энергии:

за счет упорядочения, связанного с уменьшением U;

за счет стремления системы к хаосу, сопровождающемуся увеличением энтропии S.

Так как упорядочение сопровождается уменьшением энтропии, оба механизма являются конкурирующими (т. е. противодействующими), а вклад каждого из них определяется величиной температуры.

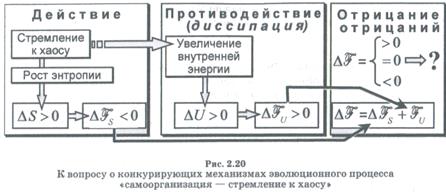Действительно, пусть в системе, представленной самой себе (т. е. δQ = 0) реализуется стремление к хаосу в соответствии с утверждением Клаузиуса. Тогда, если температура Т ≠ 0, повышение энтропии на величину ΔS > 0 должно приводить к уменьшению внутренней энергии на некоторую величину ΔF_S = -TΔS < 0, тем большую, чем выше температура Т. Однако увеличение степени хаотичности, должно обязательно привести к повышению внутренней энергии (ΔU> 0) и, следовательно, к одновременному увеличению внутренней энергии на величину
ΔF_U > 0. Таким образом, возникает конкурирующий механизм (одновременное существование действия и противодействия). Общее изменение внутренней энергии составит ΔF = ΔF_S + ΔF_U (рис. 2.20).

В результате, для системы могут реализоваться три возможности:

при температуре Т = Т_кр, для которой вклады обоих механизмов в изменение внутренней энергии равны и противоположны по знаку (|ΔU| = T_кр|ΔS|, или ΔF = 0), в системе устанавливается динамическое («подвижное»)равновесие: для части элементов системы наблюдаются процессы упорядочения, в то время как примерно столько же ранее упорядоченных элементов разупорядочивается, так что суммарная степень упорядочения системы в целом не изменяется;

при Т > Т_кр (высокие температуры) изменение энтропии и сопровождающее его изменение внутренней энергии связаны соотношением (|ΔU| < |TΔS|, доминирующим оказывается энтропийный механизм и любая система, предоставленная самой себе, стремится к «хаосу»;

3) при температурах ниже Т_кр в любой изолированной системе могут начаться процессы самоорганизации¹ (т. е. упорядочение с усложнением структуры за счет внутренних энергетических ресурсов).

Существенно, что самоорганизация за счет фазовых превращений преимущественно связана с пространственной анизотропией взаимодействий (детерминизм) между объектами системы. Для систем, в которых взаимодействие между объектами системы отсутствует, т. е. ΔU = 0, имеется только один сценарий развития — от порядка к хаосу.

2. БИФУРКАЦИИ

Как правило, усложнение (самоорганизация) системы происходит скачкообразно, или, как принято говорить, через бифуркацию.

Переход практически любой физической системы в состояние устойчивого равновесия осуществляется через колебательные процессы, которые описываются именно таким типом дифференциальных уравнений. Если диссипация отсутствует, система будет совершать незатухающие колебания относительно положения устойчивого равновесия (т.е. колебаться вечно), так и не реализовав это состояние. Если диссипация отлична от нуля, через некоторое конечное время система окажется в состоянии устойчивого равновесия. При большой и нелинейной диссипации в системе может возникнуть несколько различных состояний, отвечающих критерию относительной устойчивости (в том числе метастабильных) — возникает бифуркация.

Таким образом, наличие бифуркации в эволюции системы связано с наличием противодействия.

Поскольку в точке бифуркации реализуется состояние, не связанное однозначно с начальными условиями, иногда говорят, что бифуркация — это точка, в которой система теряет «память» о прошлом.

Примером точек бифуркации являются, например, точки фазового превращения пар — жидкость или жидкость — твердое тело. С бифуркационным характером фазовых превращений связано наличие таких специфических состояний, как переохлажденная жидкость (рис. 2.28) и переохлажденный пар, а также приведенные выше примеры возможности одного и того же элемента образовывать принципиально различные по физико-химическим свойствам материалы.

Наличие точек бифуркации отражает, прежде всего, дискретность (квантовость) свойств нашего мира, а именно — существование «кирпичиков» (порций, квантов) не только при описании свойств материальных объектов (в микромире — это элементарные частицы, в макромире — атомы и молекулы, для биологических объектов — клетка), но и для энергии, пространства, времени.

В современной биологии считают, что возникновение новых видов биоразнообразия также происходило преимущественно через бифуркацию, т.е. скачкообразно. Поэтому в археологических раскопках никому никогда не удавалось найти промежуточных состояний видов, соответствующих плавной их перестройке в соответствии с правилами естественного отбора, сформулированными Ч. Дарвином. Как невозможно в семье плавно перейти от состояния с одним ребенком к состоянию с двумя детьми, так невозможна в природе и любая пространственная взаимная ориентация составляющих систему объектов. Учитывая это, И. Пригожин в одной из своих работ отметил: Эволюция — это цепь последовательных бифуркации.

На незначительные бифуркации мы часто просто не обращаем внимания. Более значительные расцениваем как катастрофы или революции — будь то научная или научно-техническая революция или революция, связанная со сменой политических или экономических взглядов общества или государства.

Но на этом роль противодействия не заканчивается. В соответствии с первым началом термодинамики понижение внутренней энергии изолированной термодинамической системы при процессах самоорганизации должно сопровождаться обязательным выделением тепловой энергии. В результате возникает противодействие самоорганизации. Оно заключается в стремлении системы к повышению температуры путем нагревания до температуры Т_кр за счет тепла, выделяющегося в процессе самоорганизации. Поэтому если не принять специальных мер для отвода этого тепла, процесс самоорганизации может прекратиться. В этом обычно и заключается суть утверждения, что самоорганизующаяся система должна быть открытой.

Для открытых систем компенсация противодействию возможна путем отвода тепла от системы, в том числе, через излучение (как это происходит, в частности, в звездах). Так, если от смеси воды и льда при температуре 0°С не отводить тепло, процесс упорядочения молекул воды за счет кристаллизации прекратится.

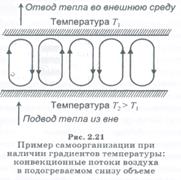
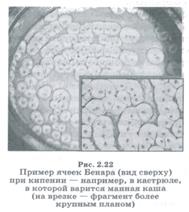
Другой пример самоорганизации — упорядочение конвекционных потоков (или образование ячеек Бенара). В этом случае необходим как подвод тепла к системе, так и его отвод (т.е. поддержание разности температур, рис. 2.21, 2.22).

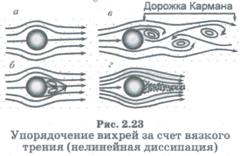Своеобразная структура упорядочения возникает при обтекании тела потоком жидкости. При относительно малых скоростях у линий тока существует «порядок» — ламинарное течение (рис. 2.23а). Однако при увеличении скорости набегающего потока упорядоченность линий тока нарушается. Сначала появляется пара вихрей (рис. 2.23б). Далее система теряет устойчивость и переходит в новый режим — турбулентного (хаотического) движения.

Однако на фоне «турбулентного хаоса» неожиданно возникает новый тип упорядочения. Вихри образуют строго упорядоченную структуру, плоский случай которой называют дорожкой Кармана (рис. 2.23в). В этом случае говорят о возникновении бифуркаций Хопфа. При дальнейшем увеличении скорости установившийся периодический режим вновь теряет устойчивость. Однако между отдельными областями течения возникают новые макроскопические связи, приводящие к установлению специфического упорядочения все более мелких масштабов. Возникает нерегулярность поведения в виде бесконечного каскада бифуркаций (рис. 2.23г). В результате с одной стороны, существенно усложняется структура течения, с другой — увеличивается его внутренняя упорядоченность.

Исходя из анализа большинства известных случаев самоорганизации, самоорганизующаяся термодинамическая система должна быть:

1) открытой (обмениваться энергией с окружающей средой);

неравновесной (в частности, заранее содержать неоднородности в виде центров конденсации или кристаллизации для фазовых превращений или иметь явно выраженные градиенты температуры, плотности, давления и пр.). В противном случае появления нового качества у системы может не случиться;

достаточно сильно флуктуирующей: всякое развитие сложной системы, выражающееся в появлении нового качества, возможно только при наличии в системе достаточно больших флуктуации или переносов масс, чтобы проявилась выраженная анизотропия взаимодействий.

Живые компоненты Земли и биосфера Земли в целом функционируют как открытые системы. Энергия излучения Солнца, кроме поддержания температуры Земли в необходимом для процессов самоорганизации температурном интервале, расходуется на создание неравновесного ее состояния за счет различного поглощения излучения Солнца в различных слоях атмосферы. Выраженные градиенты термодинамических параметров приводят к возникновению условий для проявления процессов самоорганизации.

Специального поглощения энергии или информации из вне (конечно, при наличии «зародышевых» центров) для самоорганизации не требуется. Наоборот, сами процессы самоорганизации, как правило, приводят к дополнительному выделению энергии в виде тепла, которое должно учитываться в тепловом балансе Земли.

Даже при «прямом» поглощении солнечной энергии при фотосинтезе на последующих его этапах выделяется энергии больше, чем на исходном когда энергию пришлось «занять» у Солнца, поэтому в уравнении теплового баланса для Земли, как для структурной единицы, нужно в первом приближении учитывать этот вклад:
δQ_c = δQ_смрг + δQ_з,

где δQ_c — энергия, поступающая на Землю от Солнца, δQ_смрг — энергия, выделяющаяся в биосфере за счет процессов самоорганизации, δQ_з ~Т_з⁴ —энергия, излучаемая Землей в космическое пространство в соответствии с законом Стефана-Больцмана, Т_з — средняя установившаяся (равновесная) температура Земли.

Таким образом, можно сделать вывод:

Роль Солнца в эволюционной самоорганизации живой материи во многом сводится к роли, аналогичной роли катализаторов в химических реакциях.

Отметим еще один момент. Обычно считается, что самоорганизация в закрытых системах невозможна. Одной из причин является выделение тепла при самоорганизации, описанное выше. Однако из выражения для первого начала термодинамики следует, что можно выполнить одновременно оба условия («закрытости» — δQ = 0 и стремления к упорядочению — dU < 0), если система совершает работу (δА > 0). Одним из видов такой работы является расширение системы. Именно такой сценарий, как известно, реализуется в метагалактике после Большого взрыва.

3. Эволюция Вселенной с позиций синергетики и феномен жизни.

Переживаемая нами эпоха должна служить не к разъединению, а к сближению задач об организованном и неорганизованном в природе.Не только в области жизни, но и в области неживой материи. Физико-механическая модель живой материи есть стройность.

Н. А. Умов

Рассмотрим в свете описанного в предыдущих разделах подхода механизм самоорганизации в нашей метагалактике. Исходя из приведенных выше аргументов, можно сделать вывод, что стремление системы к хаосу (саморазрушению) или порядку (самоорганизации) в значительной мере определяется соотношением между температурой системы и энергией взаимодействия между составляющими ее элементами, т.е. от соотношения между температурами системы и термодинамического равновесия. Поэтому, исходя из известных типов взаимодействий, должна существовать иерархия процессов самоорганизации как с точки зрения характера самоорганизации по мере понижения температуры системы, так и с точки зрения выделения энергии на единицу массы самоорганизующейся системы.

Если процессы самоорганизации прогрессируют, количество выделяющегося тепла, которое выступает в роли энергии противодействия, возрастает и при достижении определенной скорости процессов самоорганизации может возникнуть бифуркация.

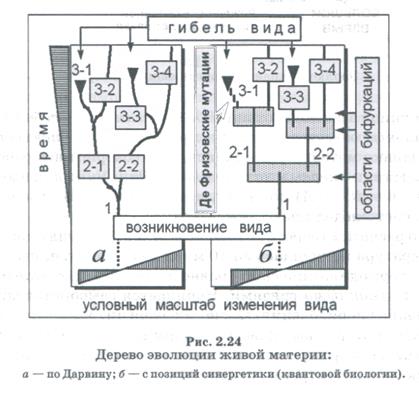
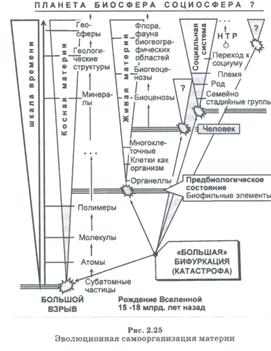
Таким образом, эволюционный процесс следует рассматривать не в виде дерева, состоящего из множества ветвей, а в виде множества отдельных ветвей, не соединяющихся с основным стволом. Частный случай такого специфического дерева приведен на рисунке 2.24. Каждая новая ветвь появляется в результате бифуркации и характеризуется появлением у реализованного в результате бифуркации состояния нового качества. Именно в результате таких бифуркаций появилась сначала живая материя, а затем и человек (см. рис. 2.25).

Рассмотрим схематично эволюционный процесс метагалактики от момента Большого взрыва до наших дней, обращая внимание лишь на наиболее значительные с позиций процессов самоорганизации вехи в эволюции Вселенной, связанные преимущественно с возникновением крупных бифуркаций^{^[2]}.

Мы пока не знаем, откуда взялась энергия Большого взрыва. Достоверно лишь одно, что примерно 18-20 млрд. лет назад в результате самой большой известной нам бифуркации образовалась материальная основа современного мира. Допустим (вполне обоснованно с позиций современных научных знаний), что по крайней мере после Большого взрыва наша метагалактика не получает никакой энергии извне.

Этап 1. В первые доли секунды после взрыва температура была столь высока, что превышала температуру термодинамического равновесия любого из известных типов взаимодействий. Единственным способом существования материальных объектов при таких условиях является состояние полного хаоса. Однако материя разлеталась, т.е. совершалась работа (δА > 0). Тогда в соответствии с первым началом термодинамики для изолированной системы (δQ = 0 = dU + δА) должна уменьшаться ее внутренняя энергия (dU < 0), т. е. система должна охлаждаться.

Этап 2. По расчетам теоретиков менее чем через секунду после Большого взрыва температура понизилась до 10 млрд. градусов, т. е. несколько ниже температуры термодинамического равновесия сильных взаимодействий, определяемых глюонными связями. Начинается самоорганизация (усложнение, появление упорядочения) за счет их энергии. У материи появляется новое качество, которое выражается в формировании объектов — элементарных частиц, т. е. формируется комбинация «кирпичиков» нашего мира — нейтроны, протоны, электроны, нейтрино^{^[3]}.

Этап 3. Примерно через 100 секунд температура упала до миллиарда градусов, достигнув, наконец, температуры термодинамического равновесия части сильных взаимодействий, связанных с пи-мезонным обменом. Возникает следующая бифуркация — начинается упорядочение барионов, т. е. формирование ядер элементов периодической системы Д. Менделеева. Около 1/4 части барионов должно было превратиться в ядра атомов гелия, тяжелого водорода (дейтерия) и других элементов. Оставшиеся нейтроны распались на протоны, т.е. превратились в ядра водорода. Всего через несколько часов образование элементов вследствие охлаждения прекратилось, и в течение примерно миллиона лет Вселенная продолжала просто расширяться и остывать.

Этап 4. Наконец, когда средняя температура метагалактики упала до нескольких тысяч градусов, т.е. понизилась ниже температуры термодинамического равновесия электромагнитных сил, электроны и ядра стали объединяться в атомы. Примерно в это же время или чуть позднее температура стала ниже температуры термодинамического равновесия гравитационных сил^{^[4]} и образовавшиеся материальные объекты начинают упорядочиваться в сферические структуры — прародители звезд и скоплений звезд (протогалактики, возможно, квазары и другие объекты), а затем и в звезды. Противодействие гравитационному упорядочению заключается в их разогреве за счет выделения энергии гравитации при сжатии облаков материальных объектов и звезд.

При достижении температуры термодинамического равновесия ядерных взаимодействий снова начинается процесс упорядочение барионов (теперь уже в массе звездного вещества) и формирование тяжелых ядер элементов периодической системы. Однако уже на этом этапе возникают проблемы. Упорядочение барионов, сопровождающееся уменьшением энергии взаимодействия, в соответствии с первым началом термодинамики, приведет к дальнейшему повышению температуры системы, в нашем случае звезды (напомним, что мы не обсуждаем эволюцию звезд в полном объеме, а отмечаем лишь некоторые важные аспекты, связанные с проявлением бифуркаций в их эволюционном развитии^{^[5]}). Это и будет противодействие процессу самоорганизации. По принципу Ле Шателье-Брауна звезда, в свою очередь, должна начать противодействовать процессу противодействия самоорганизации, т.е. найти механизмы, препятствующие повышению температуры. Один из путей — излучение тепловой энергии в окружающее пространство, что мы и наблюдаем на примере свечения звезд. Однако имеется более чем один сценарий эволюции звезды.

Количество излучаемой энергии пропорционально площади поверхности звезды, т.е. квадрату ее радиуса, а количество энергии, выделяемой за счет термоядерного синтеза элементарных частиц, — массе звезды, т.е. кубу ее радиуса. Поэтому должен существовать лишь незначительный интервал размеров звезд, для которых количество выделяемой и испускаемой энергии оказываются примерно одинаковым и их температура практически не зависит от времени до тех пор, пока все легкие элементы не будут израсходованы для синтеза тяжелых ядер. По какой-то случайности, а возможно, и закономерности (обеспечение относительной стабильности во времени физических условий на Земле, необходимых для существования живой материи) именно размеры Солнца соответствуют такому критерию.

Если масса звезды т превышает массу Солнца т_с на 20-40%, количество излучаемого тепла может оказаться меньше выделяемого внутри звезды за счет процессов самоорганизации (термоядерных реакций). Температура повышается, и у звезды остается только одна возможность противодействия — совершение работы. Энергия ядерных взаимодействий велика. Поэтому ее хватает, чтобы привести к взрыву звезды. С точки зрения введенной выше терминологии возникнет бифуркация.

Это событие в астрофизике известно под названием взрыв сверхновой звезды. Мощность взрыва оказывается, как правило, столь высока, что температура резко понижается и самоорганизация за счет ядерных сил прекращается. Сгусток материи, оставшийся после взрыва, обычно представляет плотноупакованные под действием гравитационных сил нейтроны (до плотности 10¹³-10¹⁴ г/см³), быстро вращающиеся вокруг оси (нейтронная звезда). Если масса звезды достаточно велика, остаток массы после взрыва может оказаться столь большим, что под действием гравитации сжимается до размеров, меньших радиуса сферы Шварцшильда, и на месте такой звезды появляется объект, именуемый в астрофизике черной дырой. Следует отметить, что звезда, превышающая в 2-3 раза массу Солнца, может превратиться в черную дыру и минуя точку бифуркации в виде взрыва сверхновой.

Взрыв сверхновой может происходить и по другому сценарию — за счет гравитационной энергии. Сценарий таков: к концу жизни массивной звезды в ее центре образуется железное ядро с массой около 1,4 солнечной. Ядро атома железа имеет замечательное свойство: его энергия связи в расчете на один нуклон, т. е. протон или нейтрон, максимальна среди всех ядер. Образно говоря, железо — это пепел термоядерного горения на предшествующей стадии. В некоторый критический момент давление в центре звезды уже не в силах сдерживать увеличивающийся вес ядра, равновесие между давлением и гравитацией нарушается в пользу гравитации, и ядро стремительно обрушивается на центр, образуя при этом нейтронную звезду с радиусом около 15 км. В данном случае говорят: случился гравитационный коллапс. Выделившаяся при коллапсе огромная гравитационная энергия срывает оболочку звезды ударной волной. Происходит вспышка сверхновой.

Если масса звезды окажется меньше 0,08 т_с, излучая тепловую энергию, звезда довольно быстро начнет остывать и ее эволюционное развитие за счет ядерных сил практически прекратится на стадии образования ядер легких элементов. Это так называемые несостоявшиеся звезды. Существует гипотеза, что Юпитер и Сатурн не планеты, а именно несостоявшиеся звезды со своими планетными системами.

Для звезд с массой порядка массы Солнца устанавливается динамическое равновесие между количеством выделяющегося за счет самоорганизации тепла и излучаемого поверхностью звезды. Такие звезды проходят относительно спокойно весь цикл образования ядер практически всех химических элементов, после чего звезда начнет остывать. Под действие гравитационных сил размеры звезды начнут уменьшаться (действие), а температура — снова повышаться (противодействие). Звезда начнет пульсировать, меняя размеры и яркость свечения. Например, Солнце во время одной из таких пульсаций увеличит свой радиус до размеров орбиты Земли (примерно через 5 млрд. лет), превратившись в красного гиганта. В его центре сформируется белый карлик с массой в половину солнечной. Оболочка звезды, в конце концов, рассеется и на короткое время Солнце предстанет перед мыслимым наблюдателем красивой планетарной туманностью, свечение которой будет поддерживаться ультрафиолетовым излучением горячего белого карлика.

Этап 5. Температура понижается настолько, что становится ниже температуры термодинамического равновесия для электромагнитных сил. Начинается процесс образования атомов, а при более низких температурах — молекул. На самом деле этот процесс начинается уже на 4-м этапе. За счет теплоотдачи в окружающее пространство температура поверхности звезды, как правило, оказывается значительно меньше, чем внутри. Поэтому во внешних слоях звезды за счет электромагнитных взаимодействий формируются атомы элементов. Именно наличием атомов в верхних слоях Солнца объясняют в настоящее время появление темных линий Фраунгофера в спектре его излучения.

Этап 6. В конце концов, в каком-либо месте Вселенной после образования достаточно большого числа химических элементов, начинают формироваться молекулы. Имеется несколько сортов атомов (из наиболее распространенных во Вселенной — углерод и кремний), которые могут формировать длинные цепочки (образовывать высокомолекулярные соединения — полимеры). Также как и ранее, противодействие упорядочению атомов в полимеры выражается в виде выделения тепла в окружающее пространство, которое преимущественно идет на нагрев соседних молекул, т.е. на повышение температуры.

Однако для квантовых систем, каковыми являются атомы и молекулы, имеется возможность понизить свою температуру за счет перераспределения частиц по метастабильным уровням. Число таких метастабильных уровней, как правило, увеличивается с усложнением структуры молекулы.

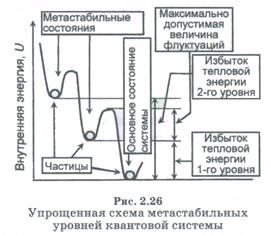При этом появляется дополнительное внутреннее энергетическое упорядочен