Тема урока. Взаимное расположение прямой и окружности». Решите задачи. Изучение нового материала.. Таким образом, прямая а и окружность имеют 2 общие точки.

Тема урока

«Взаимное расположение прямой и окружности»

Цель:

1. Рассмотреть различные случаи взаимного расположения прямой и окружности, выяснить, от чего зависит их взаимное расположение;

2. Развитие логического мышления, навыков самоконтроля;

1. Повторите определение окружности, её радиуса, диаметра и хорды.

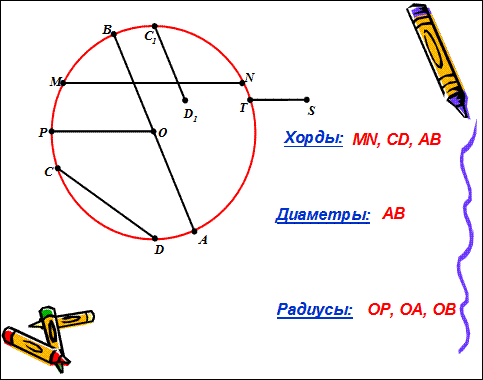
2. Решите задачи

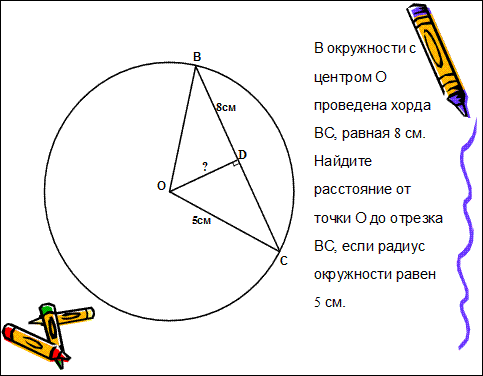
3. Повторите определение перпендикуляра и наклонной.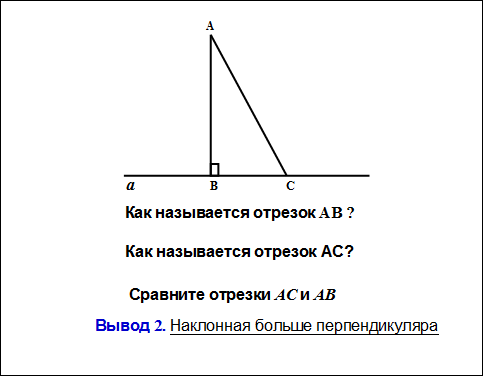

4. Изучение нового материала.

1) Подумайте, как могут располагаться по отношению друг к другу прямая и окружность, выполните чертёж;

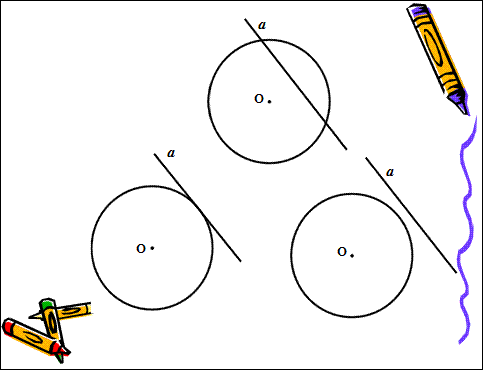
2). Задание: подумайте, почему ваши окружность и прямая пересеклись 2 раза, 1 раз, не пересеклись.

Если d<r, то прямая и окружность пересекаются 2 раза, не меньше и не больше.

Докажем это.

Пусть r – радиус окружности

d – расстояние от точки О до прямой а

а) как найти расстояние от точки О до прямой а?

ОН^а

ОН= d

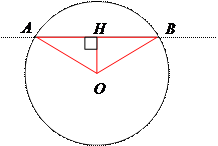б) на прямой а отложить отрезки НА=НВ=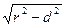

ОА²=ОН²+НА²=d²+r²- d²=r², ОА=r Þ точка А лежит на окружности.

ОВ=ОА= r Þ точка В лежит на окружности.

Таким образом, прямая а и окружность имеют 2 общие точки.

Если d=r, то окружность и прямая имеют одну общую точку.

ОН= r Þ точка Н лежит на окружности.

Единственность общей точки доказывается с помощью вывода №2.

Для любой точки М прямой а: ОН – перпендикуляр, ОМ - наклонная к прямой а Þ ОМ> ОН Þ ОМ> r Þ точка М не лежит на окружности

Если d>r, то прямая и окружность не пересекаются.

ОН> r

Для любой точки М прямой а будет верно неравенство ОМ>ОН> r (Вывод 2) Þ точка М не лежит на окружности (Вывод 1) Þ общих точек нет.

Рассмотрим случай, когда прямая проходит через центр окружности.

Подведем итоги.

12 Следующая ⇒