Решение задачи компоновки конструктивных узлов (продолжение)

Лекция 5

Решение задачи компоновки конструктивных узлов (продолжение)

Алгоритм 3 (последовательный алгоритм компоновки)

Рассмотрим простой формальный последовательный алгоритм разбиения графа G=(E,U)на заданное число кусковG₁,G₂,…,G_l,максимизирующий число ребер, входящих в выделенные куски и оперирующий с матрицей смежности Rграфа G.

Пусть граф G=(E,U) задан своей матрицей смежности R=||r_ij||, i,jÎJ=(1,2,…,n). Рассмотрим алгоритм разбиения графа на l кусков G₁,G₂,…,G_l с заданным количеством вершин в кусках t_p (p=1,l).

1. Рассмотрим строку e_iматрицы R, соответствующую вершине с максимальной локальной степеньюr(e_i)и выбираем в ней наибольший элемент r_ij, причем i¹j. Вершины e_i и e_j относим к подмножеству E₁^’ÌE₁. Переход к шагу 2.

2. Складываем поэлементно строки и столбцы e_i и e_j матрицы R. Переход к шагу 3.

3. В суммарной строке e_ij определяем максимальный элемент r_ij_,_k, k¹i, k¹j, вершину e_k относим к множеству E₁^’. Если |E₁^’|=|E₁|, то кусок сформирован. Переход к 4 . Если |E₁^’|<|E₁|, то ij принимаем за i,а k за j, и переход к шагу 2.

4. Удаляем из графа G вершины подмножества E₁ со всеми инцидентными им ребрами, т.е. вычеркиваем из матрицы строки и столбцы, соответствующие вершинам из подмножества E₁. Полученную матрицу R’ принимаем заR и переходим к 1 шагу.

5. Если в матрице R осталось ровно |E_l| строк и столбцов, то работа алгоритма закончена.

Пример алгоритма 3

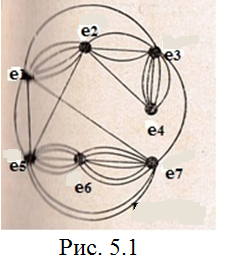
Дан граф G=(E,U) (рис. 5.1).

Необходимо разбить этот граф на 3 куска G₁=(E₁,U₁), G₂=(E₂,U₂), G₃=(E₃,U₃), содержащих по 3, 2 и 2 вершины соответственно.

Матрица смежности графа имеет вид

R=		e₁	e₂	e₃	e₄	e₅	e₆	e₇
	e₁								r(e₁)=8
	e₂								r(e₂)=9
	e₃								r(e₃)=10
	e₄								r(e₄)=6
	e₅								r(e₅)=10
	e₆								r(e₆)=11
	e₇								r(e₇)=10

Реализация алгоритма:

1. Рассмотрим строку e₆матрицы R, соответствующую вершине с максимальной локальной степеньюr(e₆)=11и выбираем в ней наибольший элемент r₆₇=6. Вершины e₆ и e₇ относим к подмножеству E₁^’={e₆,e₇}.

2. Т.к. |E₁^’|<|E₁|=3, то поэлементно суммируем строки e₆иe₇. Матрица смежности примет вид:

R =		e₁	e₂	e₃	e₄	e₅	e₆₇
	e₁							r₁₆+ r₁₇
	e₂							r₂₆+ r₂₇
	e₃							r₃₆+ r₃₇
	e₄							r₄₆+ r₄₇
	e₅							r₅₆+ r₅₇
	e₆₇							диагон. эл-ты = 0
		r₆₁+ r₇₁	r₆₂+ r₇₂	r₆₃+ r₇₃	r₆₄+ r₇₄	r₆₅+ r₇₅

3. В строке e₆₇ выбираем наибольший элементe_67,5=7. Вершину e₅ относим к подмножеству E₁^’={e₆,e₇,e₅}. Т.к. |E₁^’|=|E₁|=3, то кусок G₁ сформирован.

4. Удаляем из графа G вершины подмножества E₁ со всеми инцидентными им ребрами, т.е. вычеркиваем из исходной матрицы строки и столбцыe₆,e₇,e₅. Получаем матрицу

R^’=		e₁	e₂	e₃	e₄
	e₁					r(e₁)=5
	e₂					r(e₂)=8
	e₃					r(e₃)=9
	e₄					r(e₄)=6

5. Рассмотрим строку e₃матрицы R^’, соответствующую вершине с максимальной локальной степеньюr(e₃)=9и выбираем в ней наибольший элемент r₃₄=5. Вершины e₃ и e₄ относим к подмножеству E₂^’={e₃,e₄}. Т.к. |E₂^’|=|E₂|=2, то кусок G₂ сформирован.

6. Оставшиеся вершины e₁ и e₁относим к подмножеству E₃^’={e₁,e₂} и кусок G₃ сформирован.

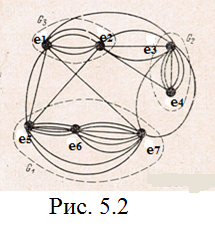
Результат разбиения графа G приведен на рис. 5.2.

Суммарное число внутренних ребер равно для полученного разбиения 22, а число соединительных ребер К=11, коэффициент разбиения ∆(G)=22/11.

Алгоритм имеет преимущества по сравнению с алгоритмом 2, если матрица смежности представляющего схему графа имеет мало нулевых элементов.

Оглавление

Лекция 5. 1

Решение задачи компоновки конструктивных узлов (продолжение) 1

Алгоритм 3 (последовательный алгоритм компоновки) 1

Пример алгоритма 3. 3