
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интервальные оценки
Интервальные оценки
1. Понятие о распределении ошибок. Вероятность
Допустим, что нас интересует некоторый параметр Х, заданный приближенным числом x. Ошибкой этого числа будет x - X. Обозначим отдельную «реализацию» этого числа через xk, причем будем предполагать, что число реализаций - экспериментальных значений - может быть какое угодно. Каждая реализация значения x будет занимать вполне определенное положение на числовой оси.
Точечной оценкой этого параметра называют единственную точку на числовой оси, которой мы по каким-либо признакам отдали предпочтение. При интервальной оценке указывают не точку, а целый интервал, внутри которого наш параметр, по-видимому, лежит с определенной долей надежности (вероятности). Основной задачей данного раздела является обоснование меры этой надежности. При этом фундаментальное значение при интервальном оценивании имеет так называемая функция распределения.
Определим функцию распределения приближенного числа х как предел отношения числа реализаций М, для которых оно лежит на числовой оси слева от некоторого фиксированного значения x0 к общему числу реализаций N. При неограниченном его увеличении аргументом функции распределения будет значение x0:
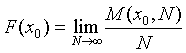
5.1.1. Свойства функции распределения
Из определения F(x) следует:
1. F(x) при любых значениях х,
2. при возрастании х функция F(x) растет,
3. если распределение параметра Х определено в конечных границах [a,b] , т.е. 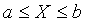 , то F(a)=0, F(b)=1
, то F(a)=0, F(b)=1
Параметр Х может быть либо непрерывным, либо дискретным. В первом случае дифференцируема. Ее производная 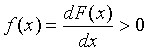 называется дифференциальной функцией распределения или плотностью вероятности.
называется дифференциальной функцией распределения или плотностью вероятности.
Последний термин легко понять, если проследить за следующими рассуждениями. По определению F(x) есть величина, равная доли всех возможных реализаций параметра Х, меньших фиксированного значения х, к общему числу реализаций. Если задан интервал [x1,x2], то доля всех реализаций, попадающих в этот интервал, называется вероятностью попадания xk в [x1,x2]. При интервальном оценивании используют также термин надежность оценивания. Мы будем принимать оба эти термина за синонимы. Общепринята следующая запись вероятности
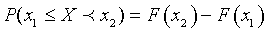
Здесь буквой P обозначена вероятность (probability), а в скобках дается ответ на вопрос «чего?». В данном случае мы утверждаем, что вероятность того, что Х лежит внутри интервала [x1,x2) равна разности функций распределения в этих точках.
Если значения x1 и x2 брать как угодно близкими друг к другу, т.е. 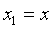 ,
, 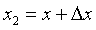 , то
, то 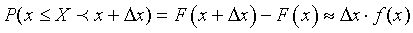 .
.
Если 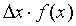 есть вероятность попадания Х в интервал
есть вероятность попадания Х в интервал 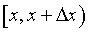 , то, естественно, f(x) - отношение этой вероятности к длине отрезка
, то, естественно, f(x) - отношение этой вероятности к длине отрезка 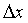 есть плотность этой вероятности. Чтобы получить вероятность на произвольном отрезке, нужно проинтегрировать плотность вероятности в пределах этого отрезка
есть плотность этой вероятности. Чтобы получить вероятность на произвольном отрезке, нужно проинтегрировать плотность вероятности в пределах этого отрезка
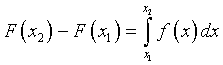
Например, если ваша интервальная оценка параметра Х есть интервал (x1,x2) с надежностью 90%, то это означает, что только 10% всех экспериментальных данных может выпасть из этого интервала
5.2. Основные законы распределения
Известно довольно большое количество различных «типовых» законов распределения случайных чисел, к каковым принадлежат и приближенные числа xk , полученные из наблюдений. В нашем курсе остановимся лишь на четырех
5.2.1. Равномерное распределение
При равномерном распределении плотность вероятности - постоянная величина, а функция распределения линейно растет от 0 до 1.
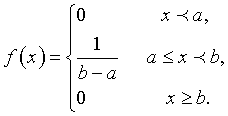 , , 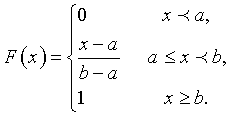 . .
|
Равномерному закону распределения подчиняются, например, ошибки округления. Рассмотрим следующий пример и ответим на вопрос: с какой надежностью можно утверждать, что целое число, полученное путем отбрасывания дробной его части, не будет иметь погрешность, по абсолютной величине превосходящую 0.5? Будем считать, что дробная часть может содержать как угодно большое число знаков. Тогда ошибку следует считать непрерывной величиной, распределенной в интервале от 0.0 до -1.0. Нужно определить вероятность 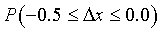 , если закон распределения имеет вид
, если закон распределения имеет вид
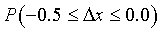
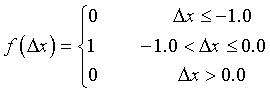
Следовательно, надежность такого утверждения равна 50%.
5.2.2. Нормальное распределение. Правило «трех сигм»
Этот закон распределения широко используется для интервальных оценок в математической обработке наблюдений. Его универсальность объясняется тем, что существует большой класс функций распределения случайной величины, который при многократном повторении трансформируется в нормальный. Например, если ошибки в 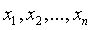 распределены по равномерному закону (например, из-за округления), то распределение ошибки среднего
распределены по равномерному закону (например, из-за округления), то распределение ошибки среднего 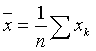 практически можно считать нормальным. То же самое, если искомая величина связана линейно с косвенными наблюдениями, число которых достаточно большое, то распределение ошибки оценки этой величины, полученной методом наименьших квадратов, также можно считать нормальным. Исключение представляют нелинейные преобразования случайной величины. В этом случае закон распределения нужно изучать особо.
практически можно считать нормальным. То же самое, если искомая величина связана линейно с косвенными наблюдениями, число которых достаточно большое, то распределение ошибки оценки этой величины, полученной методом наименьших квадратов, также можно считать нормальным. Исключение представляют нелинейные преобразования случайной величины. В этом случае закон распределения нужно изучать особо.
Дифференциальный закон нормального распределения 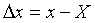 имеет вид
имеет вид
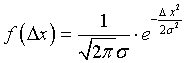
а интегральная функция распределения
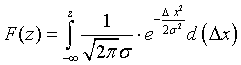
Нормальный закон распределения имеет два параметра X и 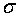 . Поэтому вместо слов «случайная (т.е. приближенная) величина х распределена по нормальному закону с математическим ожиданием (точным значением) Х и дисперсией (ошибкой)
. Поэтому вместо слов «случайная (т.е. приближенная) величина х распределена по нормальному закону с математическим ожиданием (точным значением) Х и дисперсией (ошибкой) 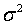 » записывают с помощью математических символов следующим образом:
» записывают с помощью математических символов следующим образом: 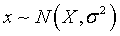 .
.
Для случайной ошибки 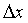 справедливо следующее утверждение:
справедливо следующее утверждение: 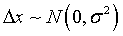
Для выполнения математических операций, связанных с нормальным законом, удобно пользоваться нормированной случайной величиной t, которая определяется следующим образом: 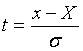 , т.е.
, т.е.  .
.
Очевидно, что математическое ожидание случайной величины t равно нулю, а дисперсия - единице:
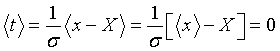
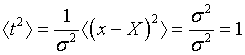
поэтому 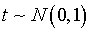 .
.
Для нормированной случайной величины t дифференциальный и интегральный законы имеют вид:
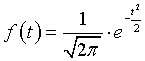
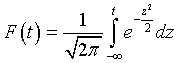
Для вычисления функции F(t) существуют таблицы. Функцию 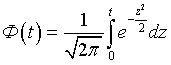 иногда называют функцией Лапласа, а
иногда называют функцией Лапласа, а 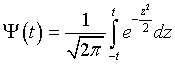 интегралом вероятностей.
интегралом вероятностей.
Для иллюстрации применения таблицы «интегралов вероятностей» вычислим вероятность «попадания» истинного значения параметра Х в интервал 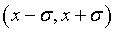 .
.
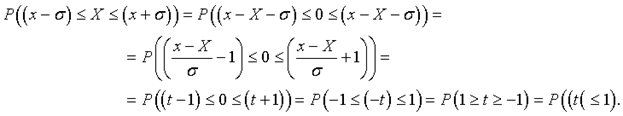
Эта вероятность равна 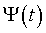 =0.683.
=0.683.
Таким образом, если результат приближенной оценки равен 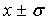 , то это означает, что надежность такой интервальной оценки 68.3%.
, то это означает, что надежность такой интервальной оценки 68.3%.
Решим другую задачу. Вместо стандартного отклонения 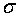 возьмем такую величину
возьмем такую величину 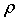 , что
, что 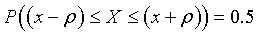 (надежность 50%).
(надежность 50%).
Из таблицы находим, что 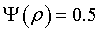 , если
, если 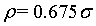
Величину 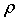 называют вероятной ошибкой. Если границы интервала определяет вероятная ошибка
называют вероятной ошибкой. Если границы интервала определяет вероятная ошибка 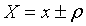 , то надежность такой интервальной оценки равна 50%.
, то надежность такой интервальной оценки равна 50%.
Оценка интервала с границами, определяемыми стандартным отклонением 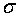 , имеет невысокую надежность: около одной трети всех экспериментальных данных «на законном основании» может быть вне этого интервала. Мы вправе увеличить надежность интервальной оценки, задавая более высокую доверительную вероятность. Чаще всего берут 0.90; 0.95 и 0.99.
, имеет невысокую надежность: около одной трети всех экспериментальных данных «на законном основании» может быть вне этого интервала. Мы вправе увеличить надежность интервальной оценки, задавая более высокую доверительную вероятность. Чаще всего берут 0.90; 0.95 и 0.99.
Например, если Pдов = 0.90, то из таблицы следует 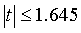 , и
, и 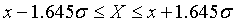 . При Pдов = 0.95 и Pдов = 0.99 соответственно получим
. При Pдов = 0.95 и Pдов = 0.99 соответственно получим 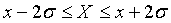 ,
, 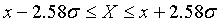
Наконец, при условии, что 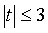 , вероятность «выпадения» наблюдательных данных очень мала и составляет 1 - 0.997 = 0.003, т.е. из тысячи значений можно ожидать, что только три будут за пределами интервала трех сигм. Эта вероятность настолько мала, что правило трех сигм часто берут в качестве критерия для отбраковки плохих данных.
, вероятность «выпадения» наблюдательных данных очень мала и составляет 1 - 0.997 = 0.003, т.е. из тысячи значений можно ожидать, что только три будут за пределами интервала трех сигм. Эта вероятность настолько мала, что правило трех сигм часто берут в качестве критерия для отбраковки плохих данных.
Необходимо подчеркнуть, что само значение 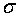 можно получить лишь при значительном числе наблюдательных данных, во всяком случае больше десяти. Реально вместо
можно получить лишь при значительном числе наблюдательных данных, во всяком случае больше десяти. Реально вместо 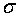 имеем среднеквадратическую ошибку
имеем среднеквадратическую ошибку 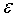 , которая сама вычисляется с ошибкой. В этом случае критерий трех сигм нужно применять с большой осторожностью. При малом числе наблюдательных данных, или, как говорят, в случае малой выборки, описанная методика интервального оценивания становится несостоятельной. Нормальный закон распределения необходимо заменить на распределение Стьюдента.
, которая сама вычисляется с ошибкой. В этом случае критерий трех сигм нужно применять с большой осторожностью. При малом числе наблюдательных данных, или, как говорят, в случае малой выборки, описанная методика интервального оценивания становится несостоятельной. Нормальный закон распределения необходимо заменить на распределение Стьюдента.
5.2.3. Распределение Стьюдента. Интервальное оценивание в случае малой выборки
Распределению Стьюдента подчиняется нормированная случайная величина t, если стандартное отклонение 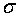 заменить на среднеквадратическую ошибку
заменить на среднеквадратическую ошибку 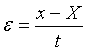 .
.
Величина 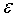 в отличие от
в отличие от 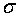 сама является случайной величиной, так как получена из конечного числа экспериментальных данных.
сама является случайной величиной, так как получена из конечного числа экспериментальных данных.
Как мы видели, для вычисления среднеквадратической ошибки измерения применяется формула
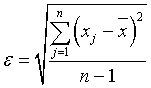
где n - 1 - число степеней свободы величины 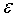 : число наблюдений минус одна связь (среднее арифметическое). Используя МНК с m неизвестными, для
: число наблюдений минус одна связь (среднее арифметическое). Используя МНК с m неизвестными, для 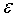 - ошибки неизвестного х - число степеней свободы равно n - m. Вообще, если число степеней свободы обозначить через k, то интегральный закон распределения случайной величины t можно записать так:
- ошибки неизвестного х - число степеней свободы равно n - m. Вообще, если число степеней свободы обозначить через k, то интегральный закон распределения случайной величины t можно записать так:
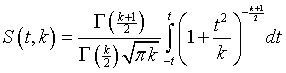
где Г(x) - гамма-функция, известная в высшей математике как специальная функция
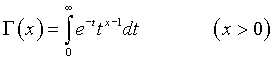
Для вычисления доверительных границ используют таблицы функции S(t,k). В качестве заданных величин берут доверительную вероятность Pдов = 1 - 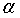 и число степеней свободы k. Таким образом, эта таблица имеет два входа: число степеней свободы k и величина
и число степеней свободы k. Таким образом, эта таблица имеет два входа: число степеней свободы k и величина 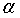 , которую называют уровнем значимости. Выходной величиной таблицы является
, которую называют уровнем значимости. Выходной величиной таблицы является 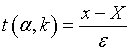 .
.
5.2.4. Распределение Пирсона. Интервальная оценка дисперсии
Распределению Пирсона или, как его еще называют, распределение хи-квадрат подчиняется cлучайная величина, полученная следующим образом
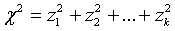
где каждая из переменных 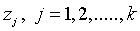 имеет среднее значение, равное нулю, дисперсию, равную единице, и распределена по нормальному закону:
имеет среднее значение, равное нулю, дисперсию, равную единице, и распределена по нормальному закону: 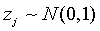 .
.
Величина 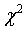 имеет k степеней свободы. Эта величина положительна и ее закон распределения определен только в положительной области аргумента:
имеет k степеней свободы. Эта величина положительна и ее закон распределения определен только в положительной области аргумента:
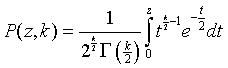
Символ 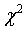 мы заменили обозначением z.
мы заменили обозначением z.
Доказано, что 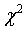 -распределению с n - 1 степенями свободы подчиняется величина
-распределению с n - 1 степенями свободы подчиняется величина
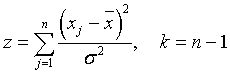
Так как квадрат среднеквадратической ошибки единичного измерения
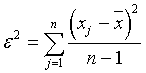 , то
, то
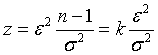
Пусть величина z подчиняется распределению Пирсона, 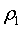 - вероятность выполнения неравенства
- вероятность выполнения неравенства 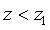 , а
, а 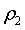 - вероятность того, что
- вероятность того, что 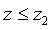 . Очевидно, что
. Очевидно, что 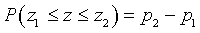 .
.
Пусть 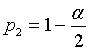 ,
, 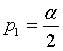 . Тогда
. Тогда 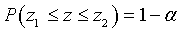 , где
, где 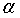 - уровень значимости.
- уровень значимости.
Для распределения Пирсона, имеются таблицы, по которым можно определить z1 и z2, задавая 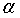 и k.
и k.
Как с помощью величин z1 и z2 получить интервальную оценку дисперсии по заданным 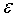 и k? Приведем последовательно эквивалентные преобразования исходного неравенства к тому, которое нас интересует:
и k? Приведем последовательно эквивалентные преобразования исходного неравенства к тому, которое нас интересует:
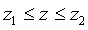 , , 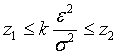 , , 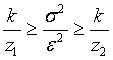 , , 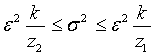 , , 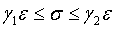 . .
|
Два последних неравенства дают нижнюю и верхнюю границы для 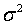 и
и 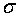 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|