
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Числовые характеристики случайных величин.
Числовые характеристики случайных величин.
Математическое ожидание - «среднее значение» случайной величиныМатематическое ожидание для .дискретной случайной величины – сумма произведений всех её значений на их вероятности.- 
Свойства мат. ожидания :
1) Математическое ожидание постоянной величины равно этой величине: М(С)=С.
Постоянный множитель можно выносить за знак математического ожидания: М(С 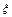 )=СМ(
)=СМ( 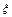 ).
).
2) Мат.ожидание суммы равно сумме мат.ожиданий: 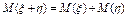 .
.
3) 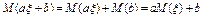
4) 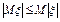
Момент n-го порядка случайной величины 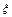 равен математическому ожиданию величины
равен математическому ожиданию величины 
М(  )=
)= 
Центральный момент n-го порядка случайной величины 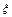 равен математическому ожиданию
равен математическому ожиданию
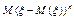
Дисперсия случайной величины - центральный момент второго порядка -равна математическому ожиданию квадрата отклонения случайной величины от её М( 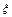 )
)
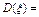
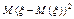
Дисперсия СВ– показатель разброса значений случайной величины вокруг её «среднего значения».
Величина, равная корню из дисперсии случайной величины называется средним квадратическим отклонением
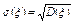
Основная формула для вычисления дисперсии

|
Доказательство: 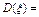
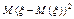 =
=  =
= 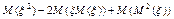 = =
= = 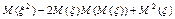 =
= 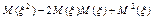 =
= 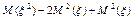
Дисперсия дискретной случайной величины -
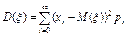 , или,
, или, 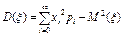
Свойства дисперсии.
1) Постоянный множитель можно вынести за знак дисперсии, возводя его в квадрат. 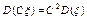
2) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
2) 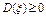 , если
, если 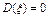 , то эта случайная величина равна константе почти наверняка (с вероятностью 1)
, то эта случайная величина равна константе почти наверняка (с вероятностью 1)
Дисперсия постоянной величины равна 0.
Доказательство: Д(С) = М((С۰М(С))2) = М(С – С)2 = М(02) = М(0) = 0
3) Дисперсия суммы двух зависимых случайных величин:
D( 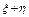 )=D(
)=D( 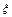 )+D(
)+D( 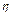 )+ 2M(
)+ 2M( 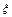 -M(
-M( 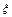 ))(
))( 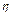 -M(
-M( 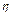 ))
))
Примеры дискретных распределений:
1) Равномерное дискретное распределение на множестве натуральных чисел 
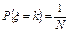 ;
; 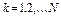 ; М(
; М( 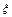 )=
)= 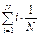
2) Геометрическое распределение с параметром р (0<p<1).
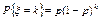 ,
, 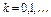 ; М(
; М( 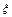 )=
)= 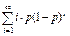 ; М(
; М( 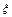 )=
)= 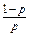 .
.
3) Биномиальное распределение :
 ,
, 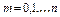 ; М(
; М( 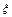 )=np, а дисперсия: D(
)=np, а дисперсия: D( 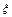 )= np(1-p)
)= np(1-p)
4) Распределение Пуассона: 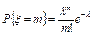 ,
, 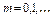 ; М(
; М( 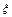 )=
)= 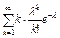 ; М(
; М( 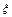 )
) 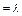
Р.S.Понятие независимости случайных величин.
Случайные величины 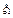 ,
, 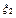 , … ,
, … , 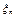 -независимы, если
-независимы, если 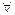 значений этих величин
значений этих величин  ,
, 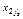 , …,
, …, 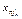 выполняется :
выполняется :
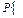
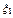 =
=  ,
, 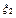 =
= 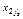 , … ,
, … , 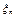 =
= 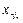

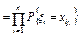 =
= 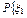 =
= 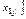
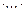
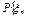 =
= 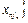
Если случайные величины 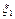 ,
,  , … ,
, … , 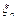 -независимы, то для них выполняется:
-независимы, то для них выполняется:
Мультипликативное свойство математического ожидания.
М( 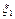 ,
, 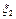 , … ,
, … , 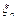 )=М(
)=М( 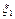 )М(
)М( 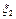 )…М(
)…М( 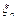 )
)
Аддитивное свойство дисперсии:
D( 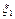 +
+ 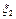 +…
+… 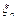 )=D(
)=D( 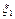 )+D(
)+D( 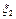 )+…+D(
)+…+D( 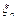 )
)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|