
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Раздел 3. Основы тригонометрии
Раздел 3. Основы тригонометрии
Тема 3.1. Тригонометрические функции и графики.
Занятие № 27. Тригонометрические функции и графики.
(Свойства и графики тригонометрических функций.)
План
| 1. Функция у=sinx, её свойства и график. |
| 2. Функция y=cosx, её свойства и график. |
| 3. Функции у= tgx, y=ctgx, их свойства и графики. |
| 4. Обратные тригонометрические функции. |
Определение: Числовые функции, заданные формулами у=sinx, y=cosx, y=tgx, y=ctgx, называют соответственно синусом, косинусом, тангенсом и котангенсом.
 
|
Функция синус.

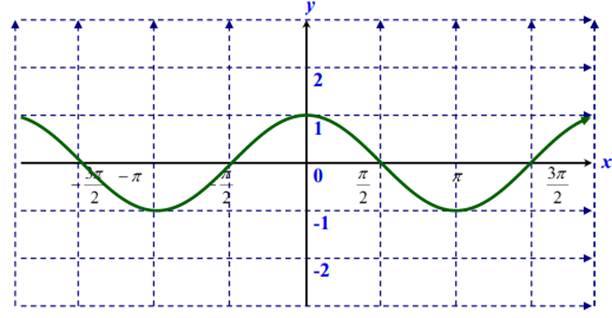
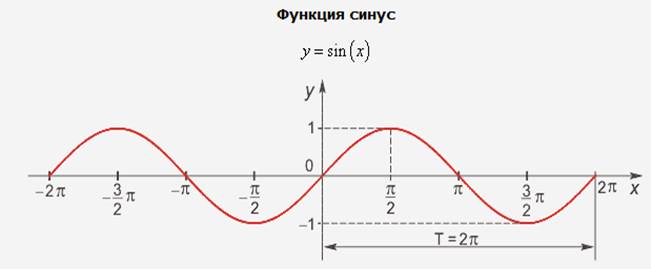
|
Функция косинус.
 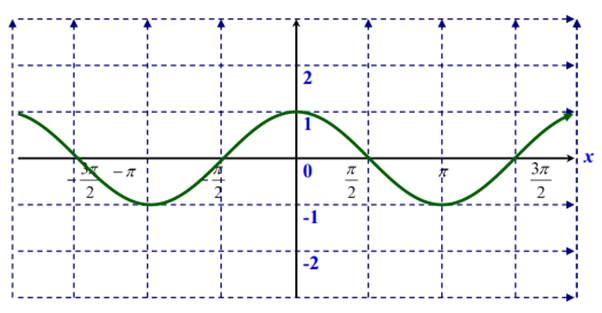
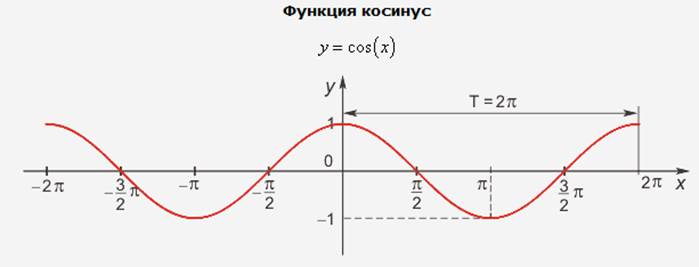
|
Функция тангенс.
 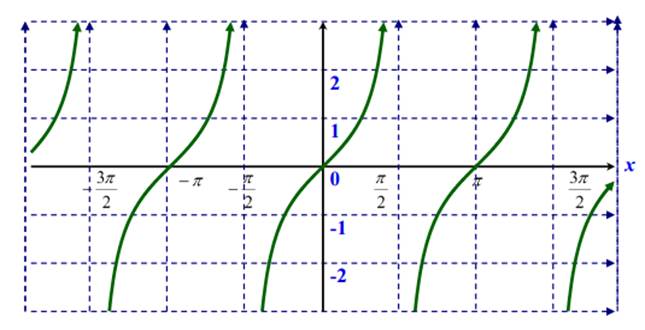
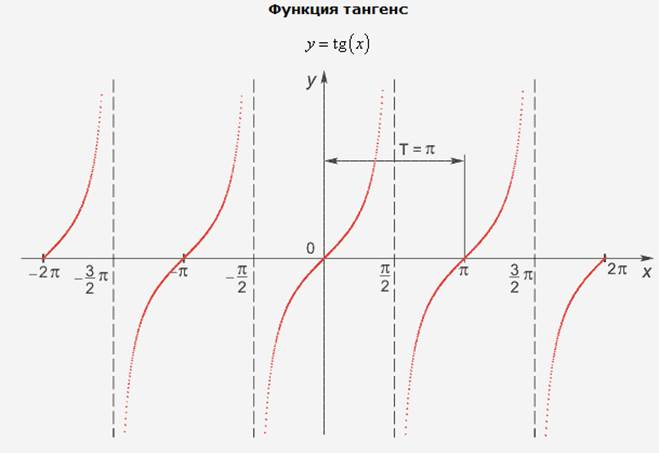
|
Функция котангенс.
 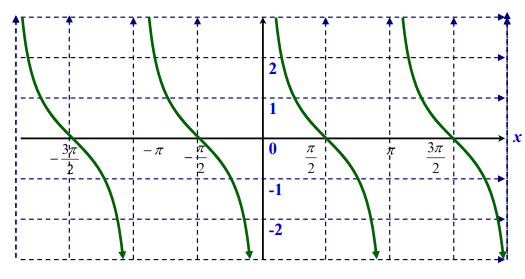
|
 Обратные функции.
1. Дадим определение обратимой функции.
Если функция у=f(х) принимает каждое своё значение только при одном значении х, то эту функцию называют обратимой.
Пусть у=f(х) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определенное число х из области её определения, такое, что f(х)=у. Это соответствие определяет функцию х от у, которую обозначим х=g(у). В этой записи в соответствии с принятыми обозначениями поменяем местами х и у.Получим у=g(х). Функцию у=g(х) называют обратной к функцииу=f(х).
2. Сформулируйте правило нахождения обратной функции.
Если у=f(х) обратима, то надо решить уравнение f(х)=у относительнох и затем поменять местами х и у.
3. Сформулируйте свойства.
1. Область определения обратной функции совпадает со множеством значений исходной функции, а множество значений обратной функции совпадает с областью определения исходной функции.
2. Обратные функции симметричны относительно прямой у=х.
Для того чтобы ввести именно обратную функцию к возведению в квадрат и было предложено понятие арифметического квадратного корня, который дает только неотрицательные значения. Т.е. для функции
Обратные функции.
1. Дадим определение обратимой функции.
Если функция у=f(х) принимает каждое своё значение только при одном значении х, то эту функцию называют обратимой.
Пусть у=f(х) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определенное число х из области её определения, такое, что f(х)=у. Это соответствие определяет функцию х от у, которую обозначим х=g(у). В этой записи в соответствии с принятыми обозначениями поменяем местами х и у.Получим у=g(х). Функцию у=g(х) называют обратной к функцииу=f(х).
2. Сформулируйте правило нахождения обратной функции.
Если у=f(х) обратима, то надо решить уравнение f(х)=у относительнох и затем поменять местами х и у.
3. Сформулируйте свойства.
1. Область определения обратной функции совпадает со множеством значений исходной функции, а множество значений обратной функции совпадает с областью определения исходной функции.
2. Обратные функции симметричны относительно прямой у=х.
Для того чтобы ввести именно обратную функцию к возведению в квадрат и было предложено понятие арифметического квадратного корня, который дает только неотрицательные значения. Т.е. для функции 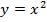 обратной функцией считается обратной функцией считается 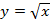 .
Аналогично существуют и функции, обратные к тригонометрическим, их называют обратными тригонометрическими функциями. К каждой из рассмотренных нами функций существует своя обратная, их называют: арксинус, арккосинус, арктангенс и арккотангенс. .
Аналогично существуют и функции, обратные к тригонометрическим, их называют обратными тригонометрическими функциями. К каждой из рассмотренных нами функций существует своя обратная, их называют: арксинус, арккосинус, арктангенс и арккотангенс.
|
Функция у = arcsinx, её свойства и график.
Рассмотрим свойства функции арксинус и построим ее график.
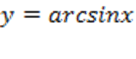 Определение. Арксинусом числа x называют такое значение угла y, для которого
Определение. Арксинусом числа x называют такое значение угла y, для которого 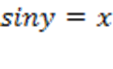 . Причем . Причем 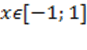 как ограничения на значения синуса, а как ограничения на значения синуса, а 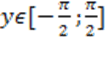 как выбранный диапазон углов.
Основные свойства арксинуса:
1) как выбранный диапазон углов.
Основные свойства арксинуса:
1) 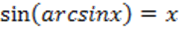 при при 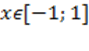 ,
2) ,
2) 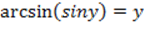 при при 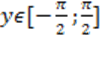 .
Основные свойства функции арксинус:
1) Область определения .
Основные свойства функции арксинус:
1) Область определения 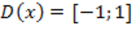 ;
2) Область значений ;
2) Область значений 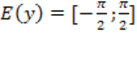 ;
3) Функция нечетная ;
3) Функция нечетная 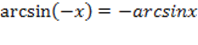 . Эту формулу желательно отдельно запомнить, т.к. она полезна для преобразований. Также отметим, что из нечетности следует симметричность графика функции относительно начала координат;
4) Функция монотонно возрастает.
Построим график функции . Эту формулу желательно отдельно запомнить, т.к. она полезна для преобразований. Также отметим, что из нечетности следует симметричность графика функции относительно начала координат;
4) Функция монотонно возрастает.
Построим график функции 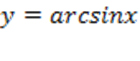 : :
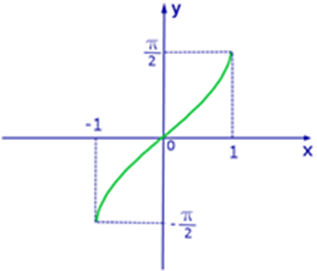 Обратим внимание, что никакой из участков графика функции не повторяется, а это означает, что арксинус не является периодической функцией, в отличие от синуса. То же самое будет относиться и ко всем остальным аркфункциям.
Обратим внимание, что никакой из участков графика функции не повторяется, а это означает, что арксинус не является периодической функцией, в отличие от синуса. То же самое будет относиться и ко всем остальным аркфункциям.
|
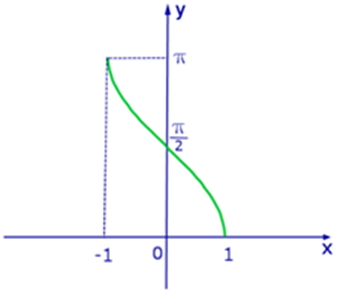
Функция y = arcosx, её свойства и график.
Рассмотрим свойства функции арккосинус и построим ее график.
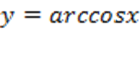 Определение. Арккосинусом числа x называют такое значение угла y, для которого
Определение. Арккосинусом числа x называют такое значение угла y, для которого 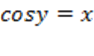 . Причем . Причем 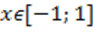 как ограничения на значения синуса, а как ограничения на значения синуса, а 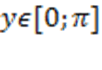 как выбранный диапазон углов.
Основные свойства арккосинуса:
1) как выбранный диапазон углов.
Основные свойства арккосинуса:
1) 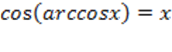 при при 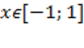 ,
2) ,
2) 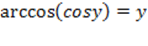 при при 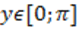 .
Основные свойства функции арккосинус:
1) Область определения .
Основные свойства функции арккосинус:
1) Область определения 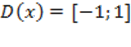 ;
2) Область значений ;
2) Область значений 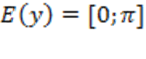 ;
3) Функция не является ни четной ни нечетной, т.е. общего вида ;
3) Функция не является ни четной ни нечетной, т.е. общего вида 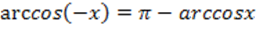 . Эту формулу тоже желательно запомнить, она пригодится нам позже;
4) Функция монотонно убывает.
Построим график функции . Эту формулу тоже желательно запомнить, она пригодится нам позже;
4) Функция монотонно убывает.
Построим график функции  : :
|
Функция y= arctgx, её свойства и график.
Рассмотрим свойства функции арктангенс и построим ее график.
 Определение. Арктангенсом числа x называют такое значение угла y, для которого
Определение. Арктангенсом числа x называют такое значение угла y, для которого 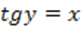 . Причем . Причем  т.к. ограничений на значения тангенса нет, а т.к. ограничений на значения тангенса нет, а 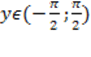 как выбранный диапазон углов.
Основные свойства арктангенса:
1) как выбранный диапазон углов.
Основные свойства арктангенса:
1) 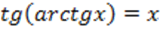 при при 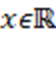 ,
2) ,
2) 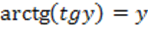 при при 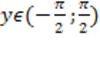 .
Основные свойства функции арктангенс:
1) Область определения .
Основные свойства функции арктангенс:
1) Область определения 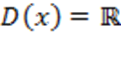 ;
2) Область значений ;
2) Область значений 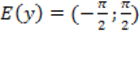 ;
3) Функция нечетная ;
3) Функция нечетная 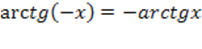 . Эта формула тоже полезна, как и аналогичные ей. Как в случае с арксинусом, из нечетности следует симметричность графика функции относительно начала координат;
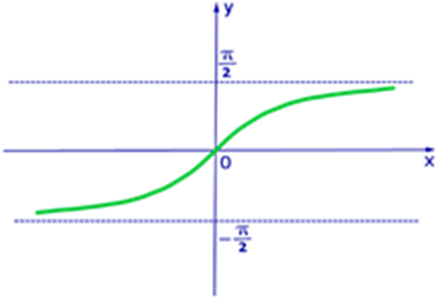
4) Функция монотонно возрастает.
Построим график функции . Эта формула тоже полезна, как и аналогичные ей. Как в случае с арксинусом, из нечетности следует симметричность графика функции относительно начала координат;
4) Функция монотонно возрастает.
Построим график функции  : :
|
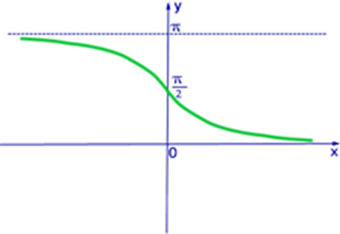
Функция y=arcctgx, её свойства и график.
Рассмотрим свойства функции арккотангенс и построим ее график.
 Определение.Арккотангенсом числа x называют такое значение угла y, для которого
Определение.Арккотангенсом числа x называют такое значение угла y, для которого 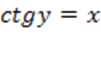 . Причем . Причем  т.к. ограничений на значения котангенса нет, а т.к. ограничений на значения котангенса нет, а 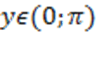 как выбранный диапазон углов.
Основные свойства арккотангенса:
1) как выбранный диапазон углов.
Основные свойства арккотангенса:
1) 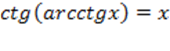 при при 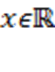 ,
2) ,
2) 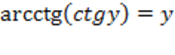 при при 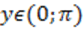 .
Основные свойства функции арккотангенс:
1) Область определения .
Основные свойства функции арккотангенс:
1) Область определения 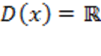 ;
2) Область значений ;
2) Область значений 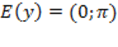 ;
3) Функция не является ни четной ни нечетной, т.е. общего вида ;
3) Функция не является ни четной ни нечетной, т.е. общего вида 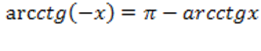 . Запомните и эту формулу, она нам тоже пригодится;
4) Функция монотонно убывает.
Построим график функции . Запомните и эту формулу, она нам тоже пригодится;
4) Функция монотонно убывает.
Построим график функции 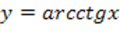 : :
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|