
Главная
Контакты
Случайная статья
|
Выполнил: Чаговец О.С.. Авторская программа по математике Л. Г. Петерсон 4 класса
Выполнил: Чаговец О.С.
Гр. ЗФ- 309-072-1-6К
|
|
Авторская программа по математике Л. Г. Петерсон 4 класса
|
| Раздел
| Понятия
| Способы действия
|
| 1.Сравнение и упорядочение чисел, знаки сравнения. Построение простейших выражений с помощью логических связок и слов; истинность утверждений.
| Неравенство. Решение неравенства. Множество решений. Строгое и нестрогое неравенство. Двойное неравенство.
| Решать неравенства вида x≥a, читать и записывать неравенства − строгие, нестрогие, двойные и др. Строить высказывания, используя логические связки «и», «или», используя знаки ≥, ≤ обосновывать и опровергать высказывания (частные, общие, о существовании). Упорядочивать информацию по заданному основанию, делить текст на смысловые части, вычленять содержащиеся в тексте основные события, устанавливать их последовательность, определять главную мысль текста, важные замечания, примеры, иллюстрирующие главную мысль и важные замечания.
Пример по теме «Решение неравенств»: Решение неравенства – это значение переменной, которое при подстановке в неравенство превращает его в верное высказывание. Так, неравенство у <9 при подстановке вместо переменной у ее числовых значений превращается в высказывание: при у = 5 оно верно (5 <9), а при у = 16 — неверно (16 <9).
Все числа по отношению к неравенству у <9 можно разделить на две группы: те из них, которые удовлетворяют данному неравенству (как, например, число 5), и те, которые ему не удовлетворяют (как число 16). Значение переменной, удовлетворяющее неравенству, называют решением неравенства. Остальные же числа решениями не являются. Таким образом, на данном уроке у учащихся должна быть сформирована способность к установлению, является данное число решением неравенства или нет
|
| 2. Способы проверки правильности вычислений.
| Оценка суммы. Оценка разности. Оценка произведения.
Прикидка результатов арифметических действий.
| Находить приближенные значения, границы суммы, разности, произведения, частного, читать, записывать, решать неравенства, текстовые задачи. Находить значения числовых и буквенных выражений при заданных значениях букв, исполнять вычислительные алгоритмы.
Пример по теме «Оценка суммы»: прочитаем неравенство: 30 <х + 4 ≤ 60.
— Назовем границы значений выражения х + 4, удовлетворяющих данному
неравенству. (От 30 до 60, причем 30 не входит, а 60 — входит.)
— Найдем наименьшее число нашего ряда, которое является решением этого неравенства. (Число 28, так как 30 <32 ≤ 60 — верно, а при подстановке 26 получим 30 <30 — неверно.)
— Почему мы считаем, что меньшего решения нет, — мы же не все числа проверили? (Если взять меньшие числа, то будет уменьшаться и сумма, поэтому она не войдет в указанный промежуток.).
— Найдите наибольшее число ряда, удовлетворяющее данному неравенству.
(Число 56, так как 30 <60 ≤ 60 — верно, а при подстановке 58 получим
30 <62 ≤60 — неверно.)
— Докажите, что большие числа ряда не подойдут. (Если подставить большее
число, то сумма увеличится и превысит 60.)
— Можете ли вы, не вычисляя, сказать, сколько чисел ряда удовлетворяют
данному неравенству? (6 чисел — от 28 до 56.)
— Какое свойство слагаемых и суммы помогло вам ответить на мои вопросы?
(Если слагаемое увеличивается, то и сумма увеличивается, а если слагаемое уменьшается, то уменьшается и сумма.)
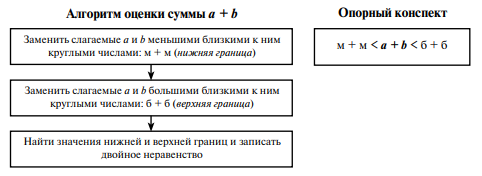
В завершение алгоритм оценки суммы фиксируется с помощью блок-схемы и опорного конспекта, например, так:
|
| 3. Алгоритмы письменного деления многозначных чисел. Площадь геометрической фигуры. Единицы площади.
| Деление с однозначным частным. Деление на двузначное число. Деление на трехзначное число. Оценка площади. Приближенное вычисление площадей.
| Знать:
1. алгоритмы письменного деления многозначных чисел, свойства деления, деление методом прикидки результата.
2.алгоритм вычисления площади фигуры неправильной формы с помощью палетки
Уметь: - устанавливать взаимосвязь между его компонентами, строить алгоритм деления, применять построенный алгоритм для вычислений, проверять правильность выполнения действий с помощью прикидки, алгоритма, вычислений на калькуляторе, решатьвычислительные примеры, текстовые задачи, уравнения и неравенства изученных типов.
- делать оценку площади, строить и применять алгоритм вычисления площади фигуры неправильной формы с помощью палетки,
решатьвычислительные примеры, текстовые задачи, уравнения и неравенства изученных типов.
Пример по теме «Прикидка результатов арифметических действий»: Нахождение приближенного значения выражения с помощью замены его компонентов числами, близкими по значению и удобными для вычислений, называется - прикидкой.
— Пользуясь смыслом умножения, найдите с помощью равенства 240 · 4 = 960 произведения чисел:
а) 240 и 5; б) 240 и 6; в) 260 и 4; г) 24 и 70. (1200, 1440, 1040, 1680.)
— Что интересного вы заметили? (Все числа четырехзначные, круглые, сумма цифр у всех — нечетная и т. д.)
— Какое число «лишнее»? Почему? (Например, 1200 — кратно 100, а остальные — нет; 1040 — нарушает закономерность, так как остальные числа последовательно увеличиваются на 240 и т. д.)
— Верно ли выполнена оценка частного: 1000: 200 <1040: 208 <1200: 300?
(Нет, так как неверно подобраны делители при вычислении верхней и нижней границ: получилось, что частное больше 5, но меньше 4.)
— Исправьте ошибки, пользуясь алгоритмом оценки частного.
(1000: 250 <1040: 208 <1200: 200, значит, 4 <1040: 208 <6.)
— Рассмотрите полученный результат. Можно ли здесь сказать, чему примерно равно значение частного? (Да, это 5, так как 5 больше 4, но меньше 6.)
— Как можно было бы быстро получить это значение, используя только делимое и делитель? (1040 — примерно 1000; 208 — примерно 200; 1000: 200 = 5.)
Следовательно, что получение приближенного результата действия с помощью замены чисел близкими по значению круглыми числами называют прикидкой.
|
| 4. Доля величины. Задачи на нахождение доли целого и целого по его доле. Площадь геометрической фигуры.
| Измерения и дроби.
Из истории дробей.
Доли. Сравнение долей.
Нахождение доли числа.
Проценты. Нахождение числа по доле. Дроби.
Сравнение дробей. Нахождение части числа. Нахождение числа по его части. Задачи на дроби. Площадь прямоугольного треугольника. Деление и дроби. Нахождение части, которую одно число составляет от другого.
| Уметь: -представление о дробях как числах, выражающих части единиц счета или измерения;
решатьстаринные задачи на дроби на основе графических моделей;
- изображать доли с помощью геометрических фигур;
-записывать, читать доли и дроби, объяснять смысл числителя и знаменателя дроби;
-сравнивать доли и дроби;
-находить долю числа и числа по его доле, решать задачи, используя правило, записывать сотые доли величины с помощью знака процента (%);
-представление об образовании дроби;
сравнивать дроби с одинаковыми знаменателями и числителями, записывать результаты сравнения с помощью знаков>, <, =;
-читать и записывать дроби в виде частного двух натуральных чисел, выражать в % дроби со знаменателем 100, наглядно изображать дробь с помощью геометрических фигур и на числовом луче;
-решать задачина нахождение части (процента) числа и числа по его части (проценту), строитьна наглядной основе алгоритм решения задач,применять его для обоснования правильности своего суждения, самоконтроля, выявления и коррекции возможных ошибок;
-решать задачи, используя формулу, составные уравнения, примеры на порядок действий;
- записывать дробь в виде частного двух натуральных чисел;
- находить часть, которую одно число составляет от другого, решать задачи, используя формулу, составные уравнения, примеры на порядок действий.
Знать: - правило нахождения доли числа, числа по его доле. Иметь представление о доле величины (половина, треть, четверть, десятая, сотая, тысячная). Процент.
-формулу площади прямоугольного треугольника;
-правило сравнения дробей с одинаковыми числителями и знаменателями;
-правила нахождения части числа, выраженной дробью и числа по его части. правило нахождения части, которую одно число составляет от другого.
Осознаватьнедостаточность натуральных чисел для практических измерений.
Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. Контролировать правильность и полноту выполнения изученных способов действий.
Пример по теме «Сравнение долей»: чем больше число, на которое делили целое, тем меньше полученная при делении доля.  , так как 2<4.
Сравним доли с помощью числового луча:
1. Расстояние от точки а числового луча до начала отсчета равно а.
2. Из двух чисел на числовом луче меньшее расположено левее, а большее —
правее. , так как 2<4.
Сравним доли с помощью числового луча:
1. Расстояние от точки а числового луча до начала отсчета равно а.
2. Из двух чисел на числовом луче меньшее расположено левее, а большее —
правее.
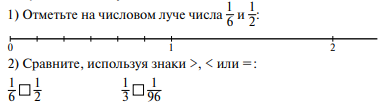 При выполнении этого задания обычно часть детей сопоставляют первое и
второе задания и верно ставят знаки, успешно пройдя предложенные мыслительные ступеньки. Другие ориентируются на правила сравнения натуральных чисел и применяют их для сравнения долей. Отсюда возникают разные позиции, которые требуют построения способа сравнения долей и их изображения на числовом луче — цель, которую должны поставить перед собой учащиеся.
При выполнении этого задания обычно часть детей сопоставляют первое и
второе задания и верно ставят знаки, успешно пройдя предложенные мыслительные ступеньки. Другие ориентируются на правила сравнения натуральных чисел и применяют их для сравнения долей. Отсюда возникают разные позиции, которые требуют построения способа сравнения долей и их изображения на числовом луче — цель, которую должны поставить перед собой учащиеся.
|
| 5. Решение текстовых задач арифметическим способом. Использование свойств арифметических действий в вычислениях.
| Сложение дробей с одинаковыми знаменателями. Вычитание дробей с одинаковыми знаменателями.
Правильные и неправильные дроби.
Правильные и неправильные части величин.
Задачи на части с неправильными дробями.
Смешанные числа.
Выделение целой части из неправильной дроби.
Запись смешанного числа в виде неправильной дроби.
Сложение и вычитание смешанных чисел.
| Знать: -правила сравнения, сложения и вычитания дробей с одинаковыми знаменателями;
- определение правильной и неправильной дроби. Способы решения задач на части;
- записывать неправильные дроби в виде смешанного числа, решать задачи на части, пользоваться формулой деления с остатком;
- алгоритм сложения и вычитания смешанных чисел, метод приведения к 1.
Уметь: - складывать, вычитать, сравнивать дроби с одинаковыми знаменателями, сравнивать дроби с одинаковыми числителями;
-различать правильные и неправильные дроби, решать примеры и задачи с дробями; решать составные уравнения;
- записывать неправильные дроби в виде смешанного числа, решать задачи на части, пользоваться формулой деления с остатком.
-выполнять действия со смешанными числами, используя рациональные приемы вычислений, метод приведения к 1, решать задачи по нахождению части числа и числа по его части.
Иметь представление о смешанном числе. Знать правило преобразования неправильной дроби в смешанное число и наоборот.
Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. Контролировать правильность и полноту выполнения изученных способов действий.
Пример по теме «Правильные и неправильные дроби»: Дробь называют правильной, если ее числитель меньше знаменателя, и неправильной, если её числитель больше или равен знаменателю.
Для открытия нового знания вначале соотносим отрезки между собой, разделив их на доли по сантиметру:
 — На сколько долей разбито наше целое — отрезок АВ? (На три доли.)
— Сколько третьих долей содержит отрезок CD? (Пять долей.)
— Какой дробью следует записать пять третьих долей? Докажите.
(
— На сколько долей разбито наше целое — отрезок АВ? (На три доли.)
— Сколько третьих долей содержит отрезок CD? (Пять долей.)
— Какой дробью следует записать пять третьих долей? Докажите.
(  — знаменатель 3 показывает, что целое разбито на три равные части, а
числитель 5 — что взяли 5 таких частей.)
— Каким действием мы могли бы найти эту дробь без чертежа, исходя из условия задачи? (Действием деления: 5: 3 = — знаменатель 3 показывает, что целое разбито на три равные части, а
числитель 5 — что взяли 5 таких частей.)
— Каким действием мы могли бы найти эту дробь без чертежа, исходя из условия задачи? (Действием деления: 5: 3 =  .)
Затем учитель предлагает детям найти по рисунку, какую часть отрезок АВ
составляет от отрезка CD. ( .)
Затем учитель предлагает детям найти по рисунку, какую часть отрезок АВ
составляет от отрезка CD. (  .) Как ее найти? (3: 5 = .) Как ее найти? (3: 5 =  .) — Чем же отличается решение задач на нахождение неправильной части величины от задач на нахождение ее правильной части? (Если часть неправильная, то дробь тоже получается неправильная, а если часть правильная — то и дробь правильная.)
Вывод соотносится с текстом учебника урока 8. Из него же учащиеся узнают принятый способ записи полученных соотношений: АВ = .) — Чем же отличается решение задач на нахождение неправильной части величины от задач на нахождение ее правильной части? (Если часть неправильная, то дробь тоже получается неправильная, а если часть правильная — то и дробь правильная.)
Вывод соотносится с текстом учебника урока 8. Из него же учащиеся узнают принятый способ записи полученных соотношений: АВ =  CD, CD = CD, CD =  АВ. АВ.
|
| 6.Планирование хода решения задачи. Представление текста задачи. Интерпретация данных таблицы.
| Шкалы. Числовой луч.
Координаты на луче. Расстояние между точками координатного луча.
Движение по координатному лучу.
Одновременное движение по координатному лучу.
| Знатьопределение числового луча, координаты точки;
- алгоритм нахождения расстояния между точками координатного луча. Иметь представление о равномерном движении точек по координатному лучу.
Уметьопределять цену деления шкалы, строить шкалы по заданной цене деления, находить число, соответствующее заданной точке на шкале. Изображать на числовом луче натуральные числа, дроби, сложение и вычитание чисел.
-определять координаты точек координатного луча, находить расстояние между ними. Изображать на числовом луче натуральны так как расстояние числа, дроби, сложение и вычитание чисел. Строить модели движения на координатном луче по формулам и таблицам.
Пример по теме «Координаты на луче»: с помощью чисел можно определить положение любой точки луча. Например, на рисунке положение точки А задается числом 4, так как расстояние от начала луча до этой точки равно 4 единичным отрезком e.
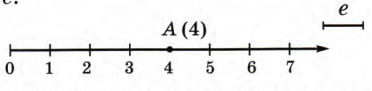 Число, равное расстоянию от точки А числового луча до начала этого луча, называют координатой точки –А и пишут А (4). Поэтому числовой луч также называют координатным лучом.
При движении точки по координатному лучу направо её координата увеличивается, а при движении налево уменьшается. Число, равное расстоянию от точки А числового луча до начала этого луча, называют координатой точки –А и пишут А (4). Поэтому числовой луч также называют координатным лучом.
При движении точки по координатному лучу направо её координата увеличивается, а при движении налево уменьшается.
|
| 7. Зависимости между величинами, характеризующими процессы движения. Скорость, время, путь.
| Скорость сближения и скорость удаления. Встречное движение. Движение в противоположных направлениях.
Встречное движение и движение в противоположных
направлениях.
Движение вдогонку.
Движение с отставанием.
Движение вдогонку и с отставанием.
Формула одновременного движения.
Задачи на одновременное движение всех типов.
| Знать:величины, уметь выполнять действия с величинами. Знать виды задач, уметь составлять схемы задач;
- виды задач, уметь составлять схемы задач;
-виды задач, уметь составлять схемы задач;
- формулу одновременного движения;
- взаимосвязь величин и их обозначение, формулу устанавливающую зависимость между этими величинами. Знать виды задач, уметь составлять схемы задач.
Уметь: -различать понятия «скорость сближения» и «скорость удаления». Наблюдать зависимости между величинами “скорость − время − расстояние” при равномерном прямолинейном движении с помощью графических моделей, фиксировать значения величин в таблицах, выявлять закономерности.Систематизироватьвиды одновременного равномерного движения двух объектов: навстречу друг другу, в противоположных направлениях, вдогонку, с отставанием;
-читать и строить модели встречного движения, находить закономерности изменения расстояния между движущимися объектами.
-читать и строить модели движения в противоположных направлениях, находить закономерности изменения расстояния в зависимости от времени движения.
- заполнять таблицы, строить формулы скорости сближения и скорости удаления объектов (vсбл. ×=v1 +v2 и vуд. ×= v1 -v2.), применять их для решения задач. Владеть навыками работы с формулами движения навстречу и в противоположных направлениях;
-читать и строить модели движения вдогонку, находить закономерности изменения расстояния между движущимися объектами;
- читать и строить модели движения с отставанием, находить закономерности изменения расстояния в зависимости от времени движения;
-заполнять таблицы, строить формулы скорости сближения и скорости удаления объектов (vсбл. ×=v1 +v2 и vуд. ×= v1 -v2.), применять их для решения задач. Владеть навыками работы с формулами движения вдогонку и с отставанием;
- строить формулу одновременного движения (s = v сбл. ∙ t встр.). Исследовать изменение расстояния между одновременно движущимися объектами.Заполнять таблицы, выводить соответствующие формулы, применять их для решения составных задач на одновременное движение;
-записывать формулу пути (s = v. t), использовать ее для решения задач на движение, моделировать и анализировать условие задач с помощью таблиц.
Пример по теме «Движение с в противоположных направлениях»:
При движении в противоположных направлениях расстояние между объектами за каждую единицу времени увеличивается на сумму скоростей 
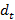 =S+ =S+  ) *t – где ) *t – где 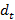 - расстояние между объектами в момент времени t, а S-первоначальное расстояние между.
При движении в противоположном направлении встреча не произойдет. - расстояние между объектами в момент времени t, а S-первоначальное расстояние между.
При движении в противоположном направлении встреча не произойдет.

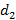 =S+ =S+  ) *2 ) *2
|
| 8. Измерение величин; сравнение и упорядочение величин. Соотношения между единицами измерения однородных величин. Единицы площади. Распознавание и изображение геометрических фигур.
| Действия над составными именованными числами.
Новые единицы площади: ар, гектар.
Действия над составными именованными числами.
Сравнение углов.
Развёрнутый угол. Смежные углы. Измерение углов.
Угловой градус.
Транспортир.
Сумма и разность углов.
Измерение углов транспортиром.
Построение углов с помощью транспортира.
Вписанный угол.
Построение углов с помощью транспортира.
Центральный угол.
Построение углов с помощью транспортира.
| Знать: -новые единицы площади: ар, гектар. Соотношения между всеми изученными единицами площади: 1 мм2; 1 см2; 1 дм2; 1м2; 1 а; 1 га; 1 км2;
-виды углов, оперировать понятиями «биссектриса», «смежные углы», «развёрнутый угол», «острый угол» и «тупой угол», владеть приёмом сравнения углов;
- назначение и способы использования транспортира, определения, вписанного и центрального углов.
Уметь: - выполнять арифметические действия над составными именованными числами. Решать вычислительные примеры, уравнения, простые и составные задачи с именованными числами. Преобразовывать именованные числа.
- распознавать и изображать развернутый угол, смежные и вертикальные углы, моделировать разнообразные ситуации расположения углов в пространстве и на плоскости, описывать их, сравнивать углы на глаз, непосредственным наложением и с помощью различных мерок.
-измерять и строитьуглы. Использовать чертёжные инструменты для выполнения построений. Проводить исследование свойств геометрических фигур с помощью измерений. Составлять выражения, формулы зависимости между величинами. Распознавать и изображать центральные и вписанные в окружность углы.
Пример по теме «Сравнение углов»:
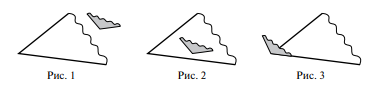
На столах у каждого учащегося вырезанные из цветной бумаги (например, желтой и синей) модели острого и тупого углов (рис. 1). Модель острого угла (желтого цвета) по площади значительно превышает модель тупого угла (синего цвета). — Сравните углы с помощью наложения.
При выполнении данного задания часть детей сориентируется на площадь моделей и, расположив тупой угол внутри острого, сделает вывод о том, что «синий» угол меньше «желтого» (рис. 2). Другая часть детей на основе проведенной подготовительной работы догадается, что сравнивать надо степень «разворота» сторон углов, и сделает вывод, что больший угол — «синий» (то есть тупой) (рис.3).
 В результате экспериментирования учащиеся должны выйти на правильный способ наложения углов, который фиксируется с помощью алгоритма и опорного конспекта, например, так:
В результате экспериментирования учащиеся должны выйти на правильный способ наложения углов, который фиксируется с помощью алгоритма и опорного конспекта, например, так:

|
| 9.Чтение столбчатой диаграммы. Создание простейшей информационной модели. Распознавание и изображение геометрических фигур (продолжение).
| Круговые диаграммы.
Столбчатые и линейные диаграммы.
Столбчатые и линейные диаграммы. Преобразование именованных чисел. Углы.
Игра «Морской бой». Пара элементов.
Передача изображений.
Координаты на плоскости.
Построение точек по их координатам.
Точки на осях координат.
Кодирование фигур на плоскости.
Координатный угол.
График движения.
Чтение графиков движения.
Изображение на графике времени и места встречи движущихся объектов.
Чтение и построение графиков движения объектов, движущихся в противоположных направлениях.
Чтение и построение графиков движения.
| Знать:понятия «круговая», «столбчатая», «линейная» диаграммы;
-понятия ««пара элементов», «координата», «координатный угол», «ось ординат», «ось абсцисс».
Уметь читать, строить, анализировать и интерпретироватьданные круговых, столбчатых и линейных диаграмм. Выполнять арифметические действия над составными именованными числами. Решать вычислительные примеры, уравнения, простые и составные задачи с именованными числами. Преобразовывать именованные числа.
-кодировать и передаватьизображения, составленные из одной или нескольких ломаных линий. Ориентироваться в координатах на плоскости.Строить графики движения по словесному описанию, формулам, таблицам. Читать, анализировать, интерпретировать графики движения, составлять по ним рассказы.Решать вычислительные примеры, текстовые задачи, уравнения и неравенства изученных типов, сравнивать и находить значения выражения на основе свойств чисел и взаимосвязей между компонентами и результатами арифметических действий.
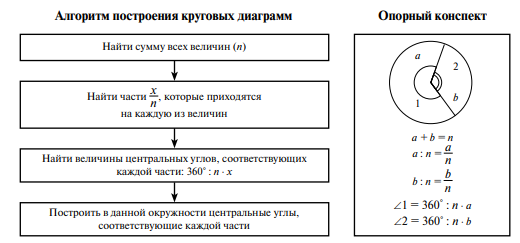
Пример по темен урока «Круговые диаграммы»: На этапе актуализации знаний надо повторить алгоритм построения центральных углов, показать пример использования центральных углов для наглядного представления на круговой диаграмме некоторой информации о жизни их класса, предложить вспомнить, где и когда им помогала наглядность или следующее индивидуальное задание: — Вода занимает 7/10 поверхности Земли, а суша — 3 /10 ее поверхности. Изобразите с помощью круговой диаграммы соотношение между площадью поверхности воды и суши на Земле.
Строим диаграмму согласно алгоритму построения круговых диаграмм.
|
| 10.Повторение
| Нумерация чисел. Арифметические действия с многозначными числами.
Решение задач. Действия с именованными числами.
Дроби. Арифметические действия с дробями.
Задачина нахождение части (процента) числа и числа по его части (проценту).
Задачи на движение.
Административная контрольная работа по итогам обучения в 4 классе
| Знать состав числа, разряды и классы многозначных чисел.
Уметь составлять выражения, записывать цифрами многозначные числа, представлять их в виде суммы разрядных слагаемых, выполнять арифметические действия с многозначными числами, находить значения выражений.
Знать величины, формулу нахождения периметра и площади, алгоритмы решения задач.
Уметь находить взаимосвязи между площадью и периметром прямоугольника (квадрата); решать текстовые задачи арифметическим способом, выполнять перевод единиц измерений.
Знатьпростые и смешанные дроби, алгоритмы выделения целой части из неправильной дроби и действий с дробями.
Уметь отмечать на числовом луче последовательность дробных чисел, записывать смешанные числа в виде неправильной дроби, выделять целую часть из неправильной дроби, решать уравнения и задачи с дробями.
Знатьправила нахождения части числа, выраженной дробью и числа по его части.
Уметьрешать задачина нахождение части (процента) числа и числа по его части (проценту), строитьна наглядной основе алгоритм решения задач,применять его для обоснования правильности своего суждения, самоконтроля, выявления и коррекции возможных ошибок.
Знать взаимосвязь величин и их обозначение, формулу устанавливающую зависимость между этими величинами. Знать виды задач, уметь составлять схемы задач.
Уметьзаписывать формулу пути (s = v. t), использовать ее для решения задач на движение, моделировать и анализировать условие задач с помощью таблиц.
|


 , так как 2<4.
Сравним доли с помощью числового луча:
1. Расстояние от точки а числового луча до начала отсчета равно а.
2. Из двух чисел на числовом луче меньшее расположено левее, а большее —
правее.
, так как 2<4.
Сравним доли с помощью числового луча:
1. Расстояние от точки а числового луча до начала отсчета равно а.
2. Из двух чисел на числовом луче меньшее расположено левее, а большее —
правее.
 При выполнении этого задания обычно часть детей сопоставляют первое и
второе задания и верно ставят знаки, успешно пройдя предложенные мыслительные ступеньки. Другие ориентируются на правила сравнения натуральных чисел и применяют их для сравнения долей. Отсюда возникают разные позиции, которые требуют построения способа сравнения долей и их изображения на числовом луче — цель, которую должны поставить перед собой учащиеся.
При выполнении этого задания обычно часть детей сопоставляют первое и
второе задания и верно ставят знаки, успешно пройдя предложенные мыслительные ступеньки. Другие ориентируются на правила сравнения натуральных чисел и применяют их для сравнения долей. Отсюда возникают разные позиции, которые требуют построения способа сравнения долей и их изображения на числовом луче — цель, которую должны поставить перед собой учащиеся.
 — На сколько долей разбито наше целое — отрезок АВ? (На три доли.)
— Сколько третьих долей содержит отрезок CD? (Пять долей.)
— Какой дробью следует записать пять третьих долей? Докажите.
(
— На сколько долей разбито наше целое — отрезок АВ? (На три доли.)
— Сколько третьих долей содержит отрезок CD? (Пять долей.)
— Какой дробью следует записать пять третьих долей? Докажите.
(  — знаменатель 3 показывает, что целое разбито на три равные части, а
числитель 5 — что взяли 5 таких частей.)
— Каким действием мы могли бы найти эту дробь без чертежа, исходя из условия задачи? (Действием деления: 5: 3 =
— знаменатель 3 показывает, что целое разбито на три равные части, а
числитель 5 — что взяли 5 таких частей.)
— Каким действием мы могли бы найти эту дробь без чертежа, исходя из условия задачи? (Действием деления: 5: 3 =  .)
Затем учитель предлагает детям найти по рисунку, какую часть отрезок АВ
составляет от отрезка CD. (
.)
Затем учитель предлагает детям найти по рисунку, какую часть отрезок АВ
составляет от отрезка CD. (  .) Как ее найти? (3: 5 =
.) Как ее найти? (3: 5 =  .) — Чем же отличается решение задач на нахождение неправильной части величины от задач на нахождение ее правильной части? (Если часть неправильная, то дробь тоже получается неправильная, а если часть правильная — то и дробь правильная.)
Вывод соотносится с текстом учебника урока 8. Из него же учащиеся узнают принятый способ записи полученных соотношений: АВ =
.) — Чем же отличается решение задач на нахождение неправильной части величины от задач на нахождение ее правильной части? (Если часть неправильная, то дробь тоже получается неправильная, а если часть правильная — то и дробь правильная.)
Вывод соотносится с текстом учебника урока 8. Из него же учащиеся узнают принятый способ записи полученных соотношений: АВ =  CD, CD =
CD, CD =  АВ.
АВ.
 Число, равное расстоянию от точки А числового луча до начала этого луча, называют координатой точки –А и пишут А (4). Поэтому числовой луч также называют координатным лучом.
При движении точки по координатному лучу направо её координата увеличивается, а при движении налево уменьшается.
Число, равное расстоянию от точки А числового луча до начала этого луча, называют координатой точки –А и пишут А (4). Поэтому числовой луч также называют координатным лучом.
При движении точки по координатному лучу направо её координата увеличивается, а при движении налево уменьшается.

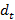 =S+
=S+  ) *t – где
) *t – где 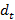 - расстояние между объектами в момент времени t, а S-первоначальное расстояние между.
При движении в противоположном направлении встреча не произойдет.
- расстояние между объектами в момент времени t, а S-первоначальное расстояние между.
При движении в противоположном направлении встреча не произойдет.

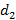 =S+
=S+  ) *2
) *2
 В результате экспериментирования учащиеся должны выйти на правильный способ наложения углов, который фиксируется с помощью алгоритма и опорного конспекта, например, так:
В результате экспериментирования учащиеся должны выйти на правильный способ наложения углов, который фиксируется с помощью алгоритма и опорного конспекта, например, так:

