Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ ПО ТЕМЕ «ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ»

ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ ПО ТЕМЕ «ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ»

Номер вариантаконтрольной работы, который необходимо выполнить студенту, соответствует порядковому номеру в списке журнала группы.

Контрольная работа оформляется в соответствие со Стандартом«Общие требования к оформлению и изложению документов учебной деятельности обучающихся», утверждѐнным приказом № 36ректора САФУ от 24.01.2018 г.

Со Стандартом подробно можно ознакомиться на сайте филиала САФУ по ссылке https://narfu.ru/upload/medialibrary/1d0/Pravila_oformlenia_rabot_34_2018.pdf.

Основные пункты из данного Стандарта:

4.1.6.Не допускается оформление документа рукописным способом (исключение составляют контрольные работы, выполненные непосредственно на аудиторных занятиях).

4.1.3.При использовании односторонней печати документа необходимо текстовый материал работы оформлять на белой бумаге формата А4, соблюдая следующие размеры поле: правое – не менее 10 мм, левое – 25 – 35 мм (в зависимости от переплѐта), верхнее – 20 мм, нижнее – не менее 20 мм.

4.1.5.Документ выполняется способом с использованием ПК и принтера: гарнитура Times New Roman; размер шрифта (кегль) – от 12 до 14 (текст выполняется единообразно одним размером шрифта во всѐм документе); междустрочный интервал

– полуторный; выравнивание – по ширине; цвет шрифта – чѐрный. Абзацы в тексте начинают отступом первой строки 12,5 мм; интервал между абзацами: до – 0 пунктов, после – 0 пунктов. Допускается применение полужирного и курсивного начертания в тексте для выделения отдельных элементов: определений, выводов и т.п.

4.1.7.Все типы работ обучающихся по программам ВО по текущему контролю успеваемости цифруются и размещаются в электронном портфолио.

Обязательными структурными элементамиконтрольной работы являются: ТИТУЛЬНЫЙ ЛИСТ, ЗАДАНИЕ, ЛИСТ ДЛЯ ЗАМЕЧАНИЙ, ОСНОВНАЯ ЧАСТЬ.

При выполнении работы в основной части сначала записывается условие задачи, затем предоставляется решение задачи с подробными пояснениями и указанием всех применяемых формул, определений, теорем и иллюстраций (чертежей, рисунков), в конце записывается ответ.

Если в работе будут ошибки, то еѐ нужно переделать по замечаниям преподавателя.

Контрольная работа не рассматриваетсяпреподавателем, если вариант не совпадает с порядковым номером в списке журнала группы.

x®¥ 8x

+ 3x - 6

2. lim tg 6x ;

x®0

3. lim

3x

x² - 3x + 2

2                 ;

x®1 x

- 4x + 3

4. lim          ;

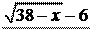x®¥ è 5x -1 ø

5. lim             .

x®2     2 - x

II. Найти производные следующих функций:

1. 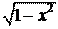y = x × arcsin x + ln      ;

1 - x²

ìx =

ï

ïî

2t - t ² ,

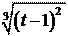1 ;

3.  y = (sin x)5ex  .

III. Провести полное исследование функции и построить еѐ график:

x³ + 4

y =      .

x2

IV. Исследовать функцию на экстремум:

z = x² + y² + 2x + 4y .

x®¥

8x + 3x

2. lim sin 6x ;

x®0

3. lim

x®2 x

3x

x³ - 8

2 - 3x + 2 ;

æ 3x

ö2 x

4.

x®¥ è 3x + 2 ø

5. 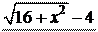lim               .

x®0         x2

II. Найти производные следующих функций:

1.

ì

ï

2. í

t ² + 1),

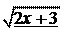ïî y = t t ² + 1;

3. y = ( x - 2)       .

x2 × e2 x

III. Провести полное исследование функции и построить еѐ график:

y = 12x .

9 + x²

IV. Исследовать функцию на экстремум:

z = x² + ( y -1)2 .

1. lim

3x² + 2x - 7

2             ;

x®¥

5x  +17

2. lim sin 5x ;

x®0

3. lim

x®2 x

2x

x² - 4

2 - 3x + 2 ;

æ 2x

ö3x+1

4.

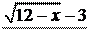x®¥ è 2x + 1 ø

5. lim             .

x®3    x - 3

II. Найти производные следующих функций:

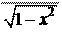
1. y = arcsin x + 1 ln 1 - x ;

2 1 + x

ìïx =

2. í

1 - t ² ,

ïî y = tg  1 + t ;

ln tg x

3. y = (tg x) 4  .

2x³ + 1

III. Провести полное исследование функции и построить еѐ график:

y =       .

x2

IV. Исследовать функцию на экстремум:

z = x² + y² - 2x - y + xy .

1. lim

3x³ + 2x - 7

2                 ;

x®¥ 5x

+ 7x + 5

2. lim sin 5x ;

x®0 sin 3x

x² + 5x + 6

3. lim

x®-2

x² + x - 2 ;

æ 2x

ö3x

4.

x®¥ è 2x - 3 ø

5. lim

x®4

12 + x - 2 8 - x .

x² -16

II. Найти производные следующих функций:

1. y =

4 + x⁴

x3

arctg x

+ 4 ;

x

ìx = ln ctg t,

2. ï

î

1 ;

cos² t

3.  y = x²⁹x  × 29^x .

x2

III. Провести полное исследование функции и построить еѐ график:

y = ( x -1)2  .

IV. Исследовать функцию на экстремум:

z = xy² (1- x - y) .

1. lim

4x³ + 6x² - 7

3             ;

x®¥

2. lim

2x + 7

5x²

2    ;

x®0 sin 4x

x² - 7x +12

3. lim

x®4  x2

æ

- 2x - 8 ;

2 ö3x

x®¥ è   ø

5. lim

x®-1

35 - x - 6 .

x² -1

II. Найти производные следующих функций:

1. 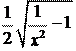y =

ìïx =

2. í

2t - t ² ,

- arccos x ;

2x²

ïî y = arcsin(t -1);

3.  y = x^{sin x}3  .

III. Провести полное исследование функции и построить еѐ график:

y = 4x .

( x + 1)2

IV. Исследовать функцию на экстремум:

z = x³ + y³ - 3xy .

1. lim

4x⁶ +16x² - 7

5                 ;

x®¥

2. lim

5x

6x²

+17x

;

x®0 sin 2x

x² + x - 6

3. lim

x®2 x2

+ 3x -10 ;

4.

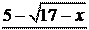x®¥ è x + 1 ø

5. lim             .

x®-8

x + 8

II. Найти производные следующих функций:

1.

ç x ÷

è   ø

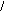ìïx = arctg e^{t 2},

2. í

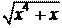ïî y = e^t + 1;

3. y = 3^x × x⁵ ×

× cos x .

x³ - 32

III. Провести полное исследование функции и построить еѐ график:

y =       .

x2

IV. Исследовать функцию на экстремум:

z = x³ + 8y³ - 6xy +1.

1. lim

x®¥

x⁵ + 70 ;

2. lim sin8x ;

x®0 sin 4x

x² + x - 6

3. lim

x®2 x2

- 7x +10 ;

x  0

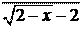5. lim

x®-2

x + 2 .

II. Найти производные следующих функций:

1. y = cos x × ln tg x - ln tg x ;

2.

í cos t

3.  y = x³x × 2^x .

III. Провести полное исследование функции и построить еѐ график:

3x⁴ + 1

y =       .

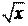x3

IV. Исследовать функцию на экстремум:

z = y

- y² - x + 6y .

1. lim

5x³ + 2x² + 8

2              ;

x®¥

x + 4

2. lim tg 4x ;

x®0 tg 5x

x² - 4x + 3

3. lim

x®1

x² -1 ;

4.

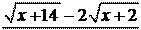x®¥ è x + 1 ø

5. lim                       .

x®2

x - 2

II. Найти производные следующих функций:

1.  y = x - ln(2 + e^x + 2  e^2x+ e^x +1);

ìx = arcsin² t,

ï

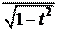
î

3.  y = (ctg3x)2ex  .

III. Провести полное исследование функции и построить еѐ график:

y = 3x - 2 .

x3

IV. Исследовать функцию на экстремум:

z = 3x + 6y - x² - xy - y² .

1. lim

5x⁴ + 7x³ - 9

2                   ;

x®¥ 8x

+ 3x - 6

2. lim tg 9x ;

x®0

3. lim

5x

x² - 3x + 2

2                 ;

x®1 x

- 4x + 3

4. lim           ;

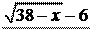x®¥ è 4x -1 ø

5. lim             .

x®2     2 - x

II. Найти производные следующих функций:

1. 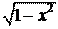y = x × arcsin x + ln      ;

1 - x²

ìx =

ï

ïî

2t - t ² ,

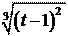1 ;

3.  y = (sin x)9ex  .

III. Провести полное исследование функции и построить еѐ график:

x³ + 4

y =      .

x2

IV. Исследовать функцию на экстремум:

z = 2x³ - xy² + 5x² + y² .

1. lim

9x² + 3x - 9

2             ;

x®¥

5x + 3x

2. lim sin18x ;

x®0

3. lim

x®2 x

5x

x³ - 8

2 - 3x + 2 ;

æ 6x

ö2 x+1

4.

x®¥ è 6x + 2 ø

5. 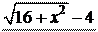lim               .

x®0         x2

II. Найти производные следующих функций:

1.

ì

ï

2. í

t ² + 1),

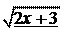ïî y = t t ² + 1;

3. y = ( x - 2)       .

x2 × e2 x

III. Провести полное исследование функции и построить еѐ график:

y = 12x .

9 + x²

IV. Исследовать функцию на экстремум:

z = x² - xy + y² + 9x - 6y + 20 .

1. lim

8x² + 2x - 7

2             ;

x®¥

3x +16

2. lim sin 4x ;

x®0

3. lim

9x²

x² - 4

2                 ;

x®2 x

- 3x + 2

æ 5x

ö6 x+1

4.

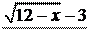x®¥ è 5x + 1 ø

5. lim             .

x®3    x - 3

II. Найти производные следующих функций:

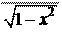
1. y = arcsin x + 1 ln 1 - x ;

2 1 + x

ìïx =

2. í

1 - t ² ,

ïî y = tg  1 + t ;

ln tg x

3. y = (tg x) 4  .

2x³ + 1

III. Провести полное исследование функции и построить еѐ график:

y =       .

x2

IV. Исследовать функцию на экстремум:

z = x² + y² + 4x + 6y .

1. lim

4x³ + 2x - 7

2                 ;

x®¥ 2x

+ 9x + 5

2. lim sin 3x ;

x®0 sin 9x

x² + 5x + 6

3. lim

x®-2

x² + x - 2 ;

æ 8x

ö4 x

4.

x®¥ è 8x - 3 ø

5. lim

x®4

12 + x - 2 8 - x .

x² -16

II. Найти производные следующих функций:

1. y =

4 + x⁴

x3

arctg x

+ 4 ;

x

ìx = ln ctg t,

2. ï

î

1 ;

cos² t

3.  y = x³¹x × 31^x .

x2

III. Провести полное исследование функции и построить еѐ график:

y = ( x -1)2  .

IV. Исследовать функцию на экстремум:

z = x² + y² - 2x - y + xy .

1. lim

4x³ + 7x² - 8

3             ;

x®¥

2. lim

6x + 7

6x²

2   ;

x®0 sin 3x

x² - 7x +12

3. lim

x®4  x2

æ

- 2x - 8 ;

8 ö4 x

x®¥ è   ø

5. lim

x®-1

35 - x - 6 .

x² -1

II. Найти производные следующих функций:

1. 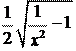y =

ìïx =

2. í

2t - t ² ,

- arccos x ;

2x²

ïî y = arcsin(t -1);

3.  y = x^{sin x}5  .

III. Провести полное исследование функции и построить еѐ график:

y = 4x .

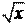( x + 1)2

IV. Исследовать функцию на экстремум:

z = y

- y² - x + 6y .

1. lim

4x⁹ +11x² - 7

8                 ;

x®¥

2. lim

9x

7x²

+17x

;

x®0 sin 14x

x² + x - 6

3. lim

x®2 x2

+ 3x -10 ;

4. lim             ;

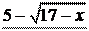x®¥ è 2x + 1 ø

5. lim             .

x®-8

x + 8

II. Найти производные следующих функций:

1.

ç x ÷

è   ø

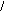ìïx = arctg e^{t 2},

2. í

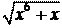ïî y = e^t + 1;

3. y = 5^x × x³ ×

× cos x .

x³ - 32

III. Провести полное исследование функции и построить еѐ график:

y =       .

x2

IV. Исследовать функцию на экстремум:

z = x³ + 8y³ - 6xy +1.

1. lim

5x⁷ + 2x² +1

7           ;

x®¥

2,5x  -10

2. lim sin 9x ;

x®0 sin 3x

x² + x - 6

3. lim

x®2 x2

- 7x +10 ;

x  0

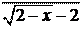5. lim

x®-2

x + 2 .

II. Найти производные следующих функций:

1. y = cos x × ln tg x - ln tg x ;

2.

í cos t

3.  y = x⁶x × 4^x .

III. Провести полное исследование функции и построить еѐ график:

3x⁴ + 1

y =       .

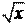x3

IV. Исследовать функцию на экстремум:

z = y

- y² - x + 6y .

x®¥

10x - 2

2. lim tg 9x ;

x®0 tg 3x

x² - 4x + 3

3. lim

x®1

x² -1 ;

4.

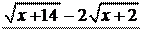x®¥ è 4x + 1 ø

5. lim                       .

x®2

x - 2

II. Найти производные следующих функций:

1.  y = x - ln(2 + e^x + 2  e^2x+ e^x +1);

ìx = arcsin² t,

ï

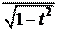
î

3.  y = (tg 4x)5ex  .

III. Провести полное исследование функции и построить еѐ график:

y = 3x - 2 .

x3

IV. Исследовать функцию на экстремум:

z = 3x + 6y - x² - xy - y² .

x®¥ 3x

+ 3x - 5

2. lim tg 4x ;

x®0

3. lim

7x²

x² - 3x + 2

2                 ;

x®1 x

- 4x + 3

4. lim           ;

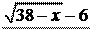x®¥ è 8x -1 ø

5. lim             .

x®2     2 - x

II. Найти производные следующих функций:

1. 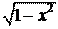y = x × arcsin x + ln      ;

1 - x²

ìx =

ï

ïî

2t - t ² ,

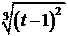1 ;

3.  y = (sin x)6ex  .

III. Провести полное исследование функции и построить еѐ график:

x³ + 4

y =      .

x2

IV. Исследовать функцию на экстремум:

z = 2x³ - xy² + 5x² + y² .

x®¥

4x + 3x

2. lim sin11x ;

x®0

3. lim

12x

x³ - 8

2                 ;

x®2 x

- 3x + 2

æ 4x

ö3x+4

4.

x®¥ è 4x -1 ø

5. 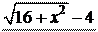lim               .

x®0         x2

II. Найти производные следующих функций:

1.

ì

ï

2. í

t ² + 1),

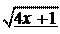ïî y = t t ² + 1;

3. y = ( x - 3)      .

x2 × e2 x

III. Провести полное исследование функции и построить еѐ график:

y = 12x .

9 + x²

IV. Исследовать функцию на экстремум:

z = x² - xy + y² + 9x - 6y + 20 .

1. lim

14x⁴ + 7x - 9

2        4      ;

x®¥  x

+ 3x -1

2. lim tg 5x ;

x®0

3. lim

13x

x² - 3x + 2

2                 ;

x®1 x

- 4x + 3

4. lim             ;

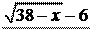x®¥ è 2x -1 ø

5. lim             .

x®2     2 - x

II. Найти производные следующих функций:

1. 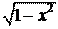y = x × arcsin x + ln      ;

1 - x²

ìx =

ï

ïî

2t - t ² ,

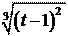1 ;

3.  y = (sin 2x)4ex  .

III. Провести полное исследование функции и построить еѐ график:

x³ + 4

y =      .

x2

IV. Исследовать функцию на экстремум:

z = x² + y² + 2x + 4y .

1. lim

4x² + 3x⁶ -10

2        4    ;

x®¥

x + 3x

2. lim sin 8x ;

x®0

3. lim

x®2 x

4x

x³ - 8

2 - 3x + 2 ;

æ x ö5 x-2

4.

x®¥ è x + 2 ø

5. 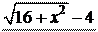lim               .

x®0         x2

II. Найти производные следующих функций:

1.

ì

ï

2. í

t ² + 1),

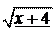ïî y = t t ² + 1;

3. y = (3x -1)   .

x3 × e3x

III. Провести полное исследование функции и построить еѐ график:

y = 12x .

9 + x²

IV. Исследовать функцию на экстремум:

z = x² + ( y -1)2 .

1. lim

4x² + 3x - 9

2             ;

x®¥

16x +17x

2. lim sin 6x ;

x®0

3. lim

x®2 x

9x

x² - 4

2 - 3x + 2 ;

æ 3x

ö4 x+2

4.

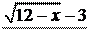x®¥ è 3x + 1 ø

5. lim             .

x®3    x - 3

II. Найти производные следующих функций:

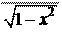
1. y = arcsin x + 1 ln 1 - x ;

2 1 + x

ìïx =

2. í

1 - t ² ,

ïî y = tg  1 + t ;

ln tg x

3. y = (tg x) 6  .

2x³ + 1

III. Провести полное исследование функции и построить еѐ график:

y =       .

x2

IV. Исследовать функцию на экстремум:

z = x² + y² - 2x - y + xy .

1. lim

8x³ + 2x - 3

2        3     ;

x®¥ x

+ 7x  + 5

2. lim sin 7x ;

x®0 sin 2x

x² + 5x + 6

3. lim

x®-2

x² + x - 2 ;

æ 7x

öx+2

4.

x®¥ è 7x - 3 ø

5. lim

x®4

12 + x - 2 8 - x .

x² -16

II. Найти производные следующих функций:

1. y =

4 + x⁴

x3

arctg x

+ 4 ;

x

ìx = ln ctg t,

2. ï

î

1 ;

cos² t

3.  y = x²⁷x × 27^x .

x2

III. Провести полное исследование функции и построить еѐ график:

y = ( x -1)2  .

IV. Исследовать функцию на экстремум:

z = xy² (1- x - y) .

1. lim

4x⁴ + 8x - 90

2                   ;

x®¥ 9x

+ 2x + 6

2. lim tg8x ;

x®0

3. lim

9x

x² - 3x + 2

2                 ;

x®1 x

- 4x + 3

4. lim          ;

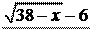x®¥ è 7x -1 ø

5. lim             .

x®2     2 - x

II. Найти производные следующих функций:

1. 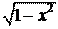y = x × arcsin x + ln      ;

1 - x²

ìx =

ï

ïî

2t - t ² ,

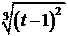1 ;

3.  y = (cos x)6ex  .

III. Провести полное исследование функции и построить еѐ график:

x³ + 4

y =      .

x2

IV. Исследовать функцию на экстремум:

z = x² + y² + 2x + 4y .

1. lim

-2x² + 7x - 9

2               ;

x®¥

5x + 9x

2.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.