
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Функция. Чётность, нечётность функций.. Периодичность функций.
Функция
Функция – зависимость одной переменной 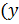 ) от другой
) от другой 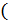 независимой
независимой 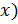 , при которой каждому значению независимой переменной
, при которой каждому значению независимой переменной 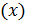 соответствует единственное значение зависимой переменной
соответствует единственное значение зависимой переменной 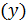
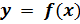
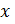 – независимая переменная – аргумент
– независимая переменная – аргумент
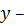 зависимая переменная – функция
зависимая переменная – функция
Область определения функции – О.О.Ф. – D(y) – все значения переменной x, при которой функция имеет смысл.
Область значений функции – О.З.Ф – E(y) – все значения зависимой переменной.
Нули функции – значение независимой переменной x, при которых значение функции равно нулю 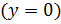
Для тригонометрических функций:
1) 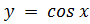 D(y): x ∈ (-∞ ; +∞)
D(y): x ∈ (-∞ ; +∞)
E(y): 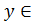 [-1;1] ; -1 ≤
[-1;1] ; -1 ≤ 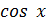 ≤ 1
≤ 1
2) 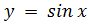 D(y): x ∈ (-∞ ; +∞) (x ∈ R)
D(y): x ∈ (-∞ ; +∞) (x ∈ R)
E(y): 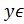 [-1;1] ; -1 ≤
[-1;1] ; -1 ≤ 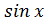 ≤ 1
≤ 1
3) 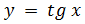 (
( 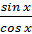 ) D(y): cos x ≠ 0
) D(y): cos x ≠ 0 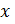 ≠
≠  + πn
+ πn
E(y): 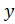 ∈ R
∈ R
4) 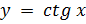 (
( 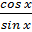 ) D(y): sin x ≠ 0
) D(y): sin x ≠ 0 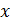 ≠ πn, n ∈ t
≠ πn, n ∈ t
E(y): 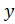 ∈ R
∈ R
Чётность, нечётность функций.
Функция y = f(x) называется чётной, если для любого x ∈ D(y) (из области определения) выполняется равенство: f(-x) = f(x)
График симметричен относительно оси Oy:
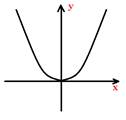
Функция y = f(x) называется нечётной, если для любого x ∈ D(y) (из области определения) выполняется равенство: f(-x) = -f(x)
График симметричен относительно оси начала координат:
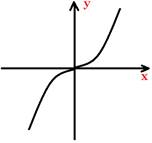
Для тригонометрических функций:
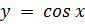 – четная:
– четная: 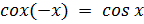
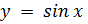 – нечетная:
– нечетная: 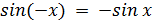
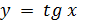 – нечетная:
– нечетная: 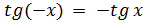
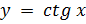 – нечетная:
– нечетная: 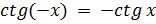
Периодичность функций.
Функция 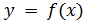 называется периодической, если существует такое число T ≠ 0, что для любого
называется периодической, если существует такое число T ≠ 0, что для любого 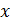 из области определения выполняется равенство:
из области определения выполняется равенство:
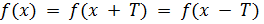
Период тригонометрических функций:
1) Для 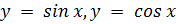 T = 2π, т.к.
T = 2π, т.к.
sin(x + 2π) = sin(x - 2π) = sin x
cos (x + 2π) = cos(x - 2π) = cos x
2) Для 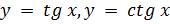 T = π, т.к.
T = π, т.к.
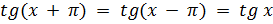
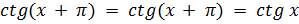
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|