Практическое занятие. Тема Применение методов математического анализа к решению задач. Закрепить и систематизировать знания обучающихся по применению производной к исследованию функций и построению их графиков. План работы. Ответьте на воп

Практическое занятие

Тема Применение методов математического анализа к решению задач

Цель.

1. Закрепить и систематизировать знания обучающихся по применению производной к исследованию функций и построению их графиков

План работы

1. Ответьте на вопросы (письменно

1. Изображён график производной. Точки х=-1, х=1, х=2 являются точками максимума.

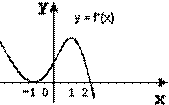
2. Производная функции в точке х_о равна 0, значит х_о - критическая точка. Верно ли?

3. Производная функции не существует в точке х_о, значит х_о - критическая точка. Верно ли?

4. Критическая точка является точкой экстремума. Верно ли?

5. Точка экстремума является критической точкой. Верно ли?

6. Функция y(x) непрерывна в точке x=4, причем y' (x)>0 на (1;4) и y'(x)<0 на (4;7). Точка x=4 является точкой минимума?

2. Историческая справка:

Именно он в 1797 г. ввёл термин «производная» что является буквальным переводом на русский язык французского слова deviree, он же ввел современные обозначения y¢, f¢. Такое название отражает смысл понятия: функция f¢(х) происходит из f(х), является производной от f(х).

Такое название отражает смысл понятия: функция f¢(х) происходит из f(х), является производной от f(х).

Если найдете экстремумы функции в каждом из заданных случаев, выпишите из таблицы буквы, которые стоят под ответом к заданию, то прочтёте фамилию этого математика (дополнительными баллами будет оценена информация о нем, оформленная отдельной страницей)

12 3 Следующая ⇒