Здравствуйте уважаемые студенты!

Урок 7-8 (17.12.21)

Здравствуйте уважаемые студенты!

Тема урока: Плоская система сходящихся сил. Решение задач.

Цель урока – закрепить теоретические знания на примерах.

Напоминаю.

Ниже даю подробную (пошаговую) методику решения задач по данной теме. Т.е. поочередно делай каждый пункт и задача решится сама. Только не запутайся с арифметикой.

Сегодня даю задачу №2 (с блокам). Перепишите методику (задачу). Эта задача чуть труднее, но методика таже.

Краткие методические указания

к решению задач.

Задачи 1 и 2.

В этих задачах требуется определить усилия в стержнях кронштейнов «методом вырезания узлов» аналитическим и графическим способами.

Прежде чем приступить к решению этих задач, нужно изучить материал тем: «Основные понятия и аксиомы статики», «Плоская система сходящихся сил». Особое внимание обратить на следующие разделы этих тем:

– связи их реакции;

– построение силового многоугольника – это вы проходили по математике;

– проекция силы на ось – правило даю ниже в книге его не ищите, его нет ;

– геометрическое условие равновесия плоской системы сходящихся сил;

– аналитические условия равновесия системы сходящихся сил – я вам дал.

Методика решения этих задач подробно изложена ниже на конкретных примерах.

И так, приступая к расчётам, студент должен знать:

- правило проекции силы на ось:

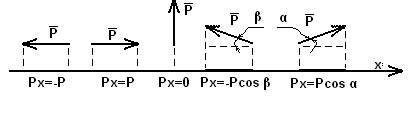
Рх – проекция силы на ось «Х». Чтобы найти проекцию силы на ось, нужно силу умножить на косинус острого угламежду направлением силы и направлением оси. Проекция имеет знак «плюс», если направление силы совпадает с направлением оси. Направление оси задаем сами.

Задача 2

Определить усилия в стержнях кронштейна. К узлу «А» прикреплен блок, через который переброшен трос. К одному концу троса прикреплен груз массой 200 кг , который удерживается в равновесии силой «Р».

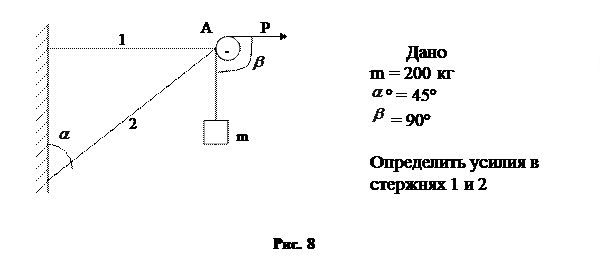
Решение

Аналитический способ

1. Мысленно вырезаем узел «А», усилия в стержнях (S₁ и S₂) направим отузла, т.е. предварительно считаем стержни 1 и 2 растянутыми.

2. Выбираем оси координат таким образом, чтобы одна из осей совпала с неизвестным усилием, например с усилием S_1.

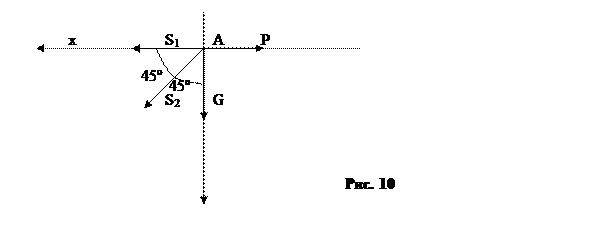
3. Рассмотрим равновесие узла «А».

Для определения неизвестных усилий S₁ и S₂ составим уравнения равновесия Σ x = 0; Σ y = 0.Значение силы «Р» принимаем равной весу G, т.к. трением на блоке пренебрегаем, т.е. P = G = mg

Тогда

(1) Σ x = 0; S₁ + S₂ cos45 – P = 0

(2) Σ y = 0; G + S₂ cos45 = 0

из (2) находим: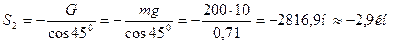

Знак «-» указывает на то, что второй стержень сжат.

Из (1) : S₁ = - S₂ cos45 + P

S₁ = - ( - 2,9 ) · 0,71 + mg = 2,05 + 2 = 4,05 кн.

Знак «+» в ответе указывает на то, что стержень 1 – растянут

Ответ: S₁ = 4,05 кн

S₂= - 2,9 кн.

Графический способ

1. Мысленно вырезаем узел «А», усилия направляем от узла, считая предварительно стержни растянутыми.

45º

2. Выбираем масштаб построения: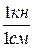

3. Произвольно выбираем центр построения точку «О»

4. Из этой точки в масштабе откладываем все заданные силы G и P (в любой последовательности). На Рис.12 есть неточности. См. рис 13.

5. Из начала (точки «о») и конца (точки «в») начатого многоугольника проводим прямые, параллельные неизвестным усилиям S₁ и S₂ до их пересечения. В результате получим точку «а».

6. Т.к. узел находиться в равновесии, силовой многоугольник должен быть замкнут. Значит, стрелки направляем по обходу силового многоугольника.

7. Определяем численные значения усилий S₁ и S₂. Для этого измеряем отрезки «aв» = |S₂| и «О» = |S₁|

8. Мысленно переносим полученные направления этих усилий с силового многоугольника(рис. 13) на вырезанный узел (рис. 11), получим знаки усилий.

Получим S₁ = 4,06 кн (отрезок «а о»)

S₂= - 2,8 кн.(отрезок «в а»)

Небольшая разница с усилиями полученным первым способом из-за погрешности в построении.

Вывод. Т.к. результаты ответов аналитического и графического способов

совпадают, задача решена верно.

До свидания!