Хелпикс

Главная

Контакты

Случайная статья



класс. Алгебра. Десятое ноября. Классная работа. Разложение квадратного трёхчлена на линейные множители. То есть, для того чтобы разложить квадратный трёхчлен на множители, надо найти его корни.(решить квадратное уравнение). ax2 + bx - c = а(х - х1)(х - х



9 класс. Алгебра

Десятое ноября

Классная работа

Разложение квадратного трёхчлена на линейные множители

На предыдущих уроках вы познакомились с квадратным трехчленом: ax2 + bx - c

Научились находить корни квадратного трёхчлена (для этого надо решить квадратное уравнение ax2 + bx - c = 0)

Сегодня на уроке вы научитесь раскладывать квадратный трёхчлен на линейные множители.

 

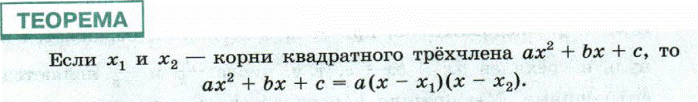
То есть, для того чтобы разложить квадратный трёхчлен на множители, надо найти его корни.(решить квадратное уравнение)

· Если квадратный трёхчлен имеет два корня, то его разложение имеет вид:

ax2 + bx - c = а(х - х1)(х - х2).

· Если квадратный трёхчлен имеет один корень, т.е. х1  = х2, то его разложение имеет вид:

ax2 + bx - c = а(х - х1)2.

· Если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители.

Рассмотрим несколько примеров.

Пример 1.Разложить на множители2х2 + 7х - 4.

По теореме 2х2 + 7х - 4 = 2(х-х1)(х-х2).

Найдем корни квадратного трёхчлена:

 

2х2 + 7х - 4=0

a=2, b =7, c=-4

D = b2 - 4ac=49+32 = 81>0, два корня 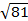=9

х1 =  =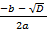

x2=  =

Получим, разложение

2х2 + 7х - 4 = 2(х - (-4))(х - ) = 2(х + 4) (х - ) = (х + 4)(2х - 2· ) = (х+4)(2х-1)

Ответ: (х+4)(2х-1)

Пример 2. Сократить дробь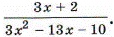

 

Разложим квадратный трёхчлен 3х2 - 13х - 10 на множители. Найдём корни

3х2 - 13х - 10 = 0

D = 169 +120 = 289>0,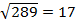

х1 =  =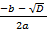

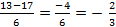
x2=  =

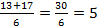
Получим 3х2 - 13х - 10 = 3(х - (-  ))(х - 5) = (3х + 2)(х - 5)

 

Значит, =

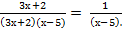
Ответ: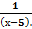

Теорему, пример1 и пример 2 записать в тетрадь.

Видеоурок можно посмотреть по ссылке https://resh.edu.ru/subject/lesson/1991/main/

ИТОГ: Сегодня на уроке вы изучили правило разложения квадратного трёхчлена на множители и рассмотрели основные типы задач.

 

Домашнее задание.Выучить теорему п.4, стр.27. Решить № 76 (ж,з,и), № 84.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.