Функцияy=f(x),x∈Xявляется обратимой, если любое своё значение она имеет только в одной точке множестваX(когда разным значениям аргумента соответствуют разные значения функции).. Теорема 1. Теорема 2. Теорема 3

Функцияy=f(x),x∈Xявляется обратимой, если любое своё значение она имеет только в одной точке множестваX(когда разным значениям аргумента соответствуют разные значения функции).

Теорема 1

Если функция y=f(x), x∈X монотонна на множестве X, то она обратима.

Пусть функция y=f(x), x∈X является обратимой, и E(f)=Y. Каждому y из Y соответствует единственное значение x, при котором f(x)=y. Тогда получим функцию, определённую на Y и имеющую значения на множестве X. Таким образом построенная функция будет являться обратной по отношению к функции y=f(x), x∈X, и её обозначают x=f−1(y),y∈Y.

Теорема 2

Если функция y=f(x) возрастает на множестве X, и область значений функции есть множество Y, то обратная функция x=f−1(y),y∈Y возрастает на множестве Y.

Или,

если функция y=f(x) убывает на множестве X, и область значений функции есть множество Y, то обратная функция x=f−1(y),y∈Y убывает на множестве Y.

Теорема 3

Точки M(a;b) и P(b;a) симметричны относительно прямой y=x.

Нахождение формулы для функции, обратной данной

Пользуясь формулой y=f(x), следует выразить x через y, а в полученной формуле x=g(y) заменить x на y, а y на x.

Пример:

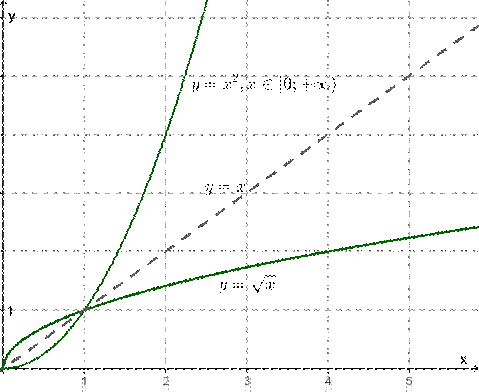
найти функцию, обратную для функции y=x2,x∈[0;+∞).

Функция y=x2 возрастает на промежутке [0;+∞). Делаем вывод, что обратная функция существует. Если значения x принадлежат промежутку [0;+∞), то x=y–√. Заменим x на y, а y на x, получим обратную функцию y=x−−√,x∈[0;+∞). Обратная функция определена на промежутке [0;+∞) и её график симметричен графику функции y=x2,x∈[0;+∞) относительно прямой y=x.