Теоретический материал

Тема урока: «Степенная функция. Её свойства и график»

Цель урока: познакомиться со свойствами и графиками различных ( в зависимости от показателя степени) видов степенной функции, формировать навыки свободного чтения графиков, умение отражать свойства функции на графике.

Теоретический материал

Если показатель степени n — натуральное число, то степенная функция задаётся формулой y=xn.

При n=1, y=x1 или y=x — прямая.

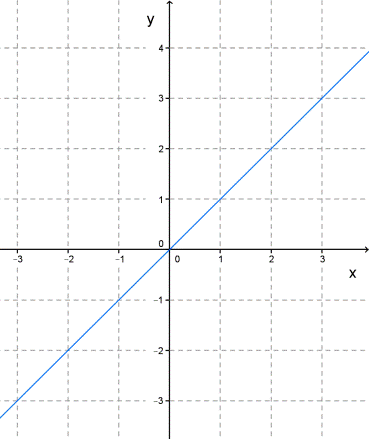
При n=2, y=x2 — парабола.

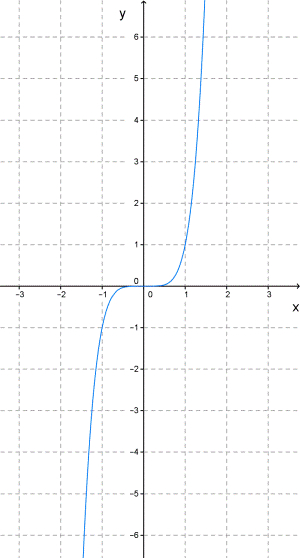
При n=3, y=x3 — кубическая парабола.

График степенной функции y=xn, где n — чётное число (4, 6, 8...), принимает вид параболы.

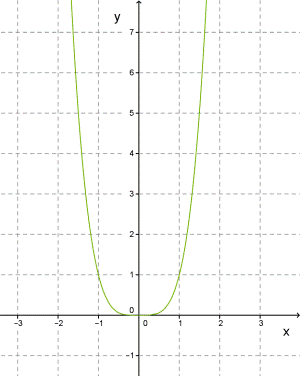
График степенной функции y=xn, где n — нечётное число (5, 7, 9...), принимает вид кубической параболы.

Если показатель степени — целое отрицательное число, то степенная функция задаётся формулой y=x−n или y=1xn.

График степенной функции y=x−n в случае, когда n — чётное число (4, 6, 8...), принимает вид:

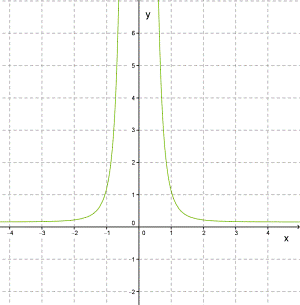
Например, такой вид принимают графики функций y=x−4,y=x−8.

График степенной функции y=x−n в случае, когда n — нечётное число (5, 7, 9...), принимает вид гиперболы:

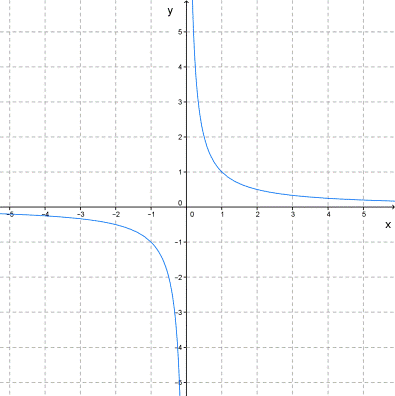
Например, такой вид принимают графики функций y=x−5,y=x−11.

Рассмотрим графики степенных функций y=xmn с положительным дробным показателемmn.

1. Степенная функция y=xmn, где mn>1 — неправильная дробь. Графиком является положительная ветвь параболы.

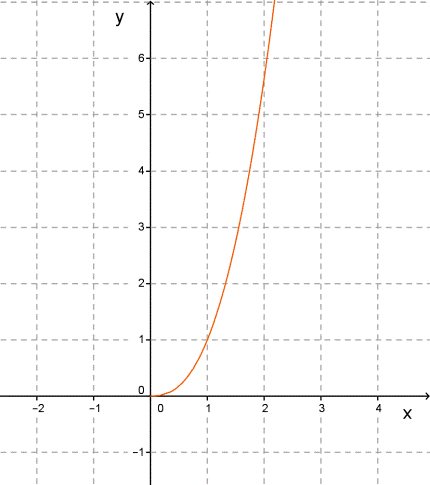
Свойства функции y=xmn, где mn>1:

1.D(f)=[0;+∞);

2.E(f)=[0;+∞);

3. функция ни чётная, ни нечётная;

4. возрастает при x∈[0;+∞);

5. yнаим.=0;

6. ограничена снизу;

7. выпукла вниз;

8. непрерывна.

2. Степенная функция y=xmn, где 0<mn<1 — правильная дробь.

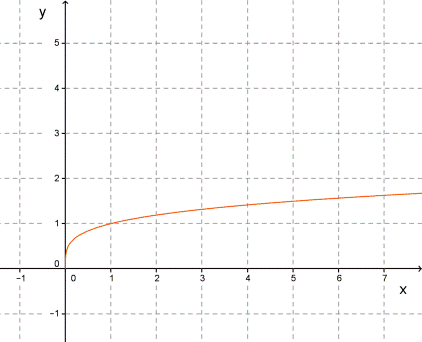
Свойства функции y=xmn, где 0<mn<1:

1.D(f)=[0;+∞);

2.E(f)=[0;+∞);

3. функция ни чётная, ни нечётная;

4. возрастает при x∈[0;+∞);

5. yнаим.=0;

6. ограничена снизу;

7. выпукла вверх;

8. непрерывна.

График — положительная ветвь гиперболы.

Горизонтальная асимптота графика — прямая у=0 и вертикальная асимптота — прямая х=0.

Свойства функции y=x−mn:

1.D(f)=(0;+∞);

2.E(f)=(0;+∞);

3. ни чётная, ни нечётная;

4. убывает на промежутке x∈(0;+∞);

5. нет наибольшего и наименьшего значений;

6. ограничена снизу;

7. выпукла вниз;

8. непрерывна.

12 Следующая ⇒