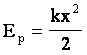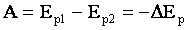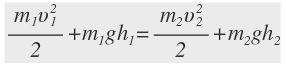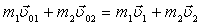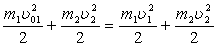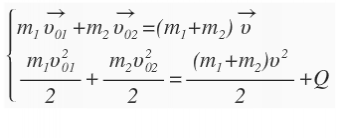Главная
Контакты
Случайная статья
|
Потенциальная энергия тел, взаимодействующих посредством гравитационных сил.
Потенциальная энергия тел, взаимодействующих посредством гравитационных сил.
|
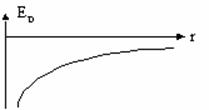
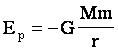 , где r- расстояние между взаимодействующими телами.
Знак "-" говорит о том, что это энергия притягивающихся тел.
При сближении тел потенциальная энергия увеличивается по модулю.
Работа по сближению двух астрономических объектов: , где r- расстояние между взаимодействующими телами.
Знак "-" говорит о том, что это энергия притягивающихся тел.
При сближении тел потенциальная энергия увеличивается по модулю.
Работа по сближению двух астрономических объектов: 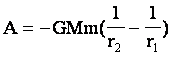 . .
| 
|
|
Потенциальная энергия упруго деформированного тела. Работа силы упругости.
|
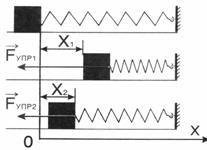
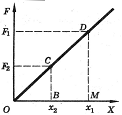
Для вывода формулы используем, что работа численной равна площади под графиком зависимости силы от координаты. При малых упругих деформациях сила упругости прямо пропорциональна абсолютной деформации (з-н Гука) - см. рис.
Тогда работа при изменении деформации от х1 до х2 равна: 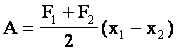 . .
| 
|
Учитывая з-н Гука, получим: 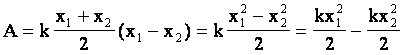
| 
|
Т.о., если принять за потенциальную энергию упруго деформированного тела величину 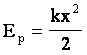 ,
где k - коэффициент жесткости, а х - абсолютная деформация тела, то можно сделать вывод , что ,
где k - коэффициент жесткости, а х - абсолютная деформация тела, то можно сделать вывод , что 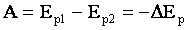 ,
т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком. ,
т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком.
| 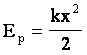
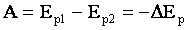
|
| Работа силы упругости зависит только от координат (начальной и конечной деформаций) тела и, следовательно, не зависит от траектории. Работа по замкнутой траектории равна нулю.
|
|
| Консервативные силы.
Консервативными (сохраняющими) наз. силы, работа которых не зависит от траектории и по замкнутой траектории равна нулю (эти силы не зависят от скоростей). Примеры: гравитационные, упругие.
|
|
| Диссипативные силы
Диссипативными (рассеивающими) наз. силы, работа которых зависит от траектории и по замкнутой траектории не равна нулю (такие силы зависят от скорости). Пример: сила трения.
|
|
|
Закон сохранения механической энергии.
|
| Сумма кинетической и потенциальной энергий системы тел называется полной механической энергиейсистемы.
| E = Ep + Ek
|
| Учитывая, что при совершении работы A = ΔEk и, одновременно, A = - ΔEp, получим: ΔEk = - ΔEp или Δ(Ek + Ep)=0 – изменение суммы кинетической и потенциальной энергий (т.е. изменение полной механической энергии) системы равно нулю.
| ΔEk = - ΔEp
|
| Значит, полная энергия системы остается постоянной:
E = Ep + Ek = const.
В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется. (Или: полная механическая энергия системы тел, взаимодействующих силами упругости и гравитации, остается неизменной при любых взаимодействиях внутри этой системы).
| E = Ep + Ek = const
|
| Например, для тела, движущегося под действием силы тяжести (падение; тело, брошенное под углом к горизонту, вертикально вверх или движущееся по наклонной плоскости без трения):
| 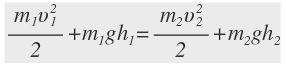
|
|
Работа силы трения и механическая энергия.
|
| Если в системе действуют силы трения (сопротивления), которые не являются консервативными, то энергия не сохраняется. При этом E1 - E2 = Aтр. Т.е. изменение полной механической энергии системы тел равно работе сил трения (сопротивления) в этой системе. Энергия изменяется, расходуется, поэтому такие силы наз.диссипативными (диссипация – рассеяние).
| E1 - E2 = Aтр
|
| Т.о. механическая энергия может превращаться в другие виды энергии, напр., во внутреннюю(деформация взаимодействующих тел, нагревание).
|
|
Столкновения тел.
|
| З-н сохранения и превращения механической энергии применяется, например, при изучении столкновений тел. При этом он выполняется в системе с з-ном сохранения импульса. Если движение происходит так, что потенциальная энергия системы остается неизменной, то может сохраняться кинетическая энергия.
|
| Удар, при котором сохраняется механическая энергия системы, наз. абсолютно упругим ударом.
| 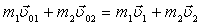 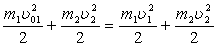
|
| Удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью, наз. абсолютно неупругим ударом (при этом механическая энергия не сохраняется – деформация, тепло).
| 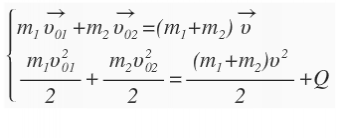
|
| Удар, при котором тела до соударения движутся по прямой, проходящей через их центр масс, наз. центральным ударом.
|
|

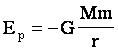 , где r- расстояние между взаимодействующими телами.
Знак "-" говорит о том, что это энергия притягивающихся тел.
При сближении тел потенциальная энергия увеличивается по модулю.
Работа по сближению двух астрономических объектов:
, где r- расстояние между взаимодействующими телами.
Знак "-" говорит о том, что это энергия притягивающихся тел.
При сближении тел потенциальная энергия увеличивается по модулю.
Работа по сближению двух астрономических объектов: 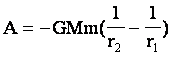 .
.

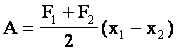 .
.

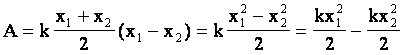

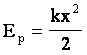 ,
где k - коэффициент жесткости, а х - абсолютная деформация тела, то можно сделать вывод , что
,
где k - коэффициент жесткости, а х - абсолютная деформация тела, то можно сделать вывод , что 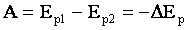 ,
т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком.
,
т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком.