октября 2021 г. (среда) . Модели оптимального планирования

13 октября 2021 г. (среда)

Дисциплина: Информатика и ИКТ

Группа: № 78

Урок № 19

Тема: Модели оптимального планирования.

Цель: получить представлене о моделях оптимального планирования.

Учебник: Информатика. Базовый уровень : ученик для 11 класса / И.Г. Семакин, Е.К. Хеннер, Т.Ю. Шеина. – 5-е изд. – М. : БИНОМ. Лаборатория знаний, 2015. – 224 с. : ил.

Модели оптимального планирования

Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец государства. Постановка задачи планирования выглядит следующим образом :

• имеются некоторые плановые показатели : Х, У, и др . ;

• имеются некоторые ресурсы: R l , R2 и др . , за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;

• имеется определенная стратегическая цель, зависящая от значений Х, У и др. плановых показателей, на которую следует ориентировать планирование.

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Если мы хотим использовать компьютер для решения задачи оптимального планирования, то нам снова нужно построить математическую модель. Следовательно, задача планирования должна быть переведена на язык чисел , формул , уравнений и других средств математики . В полном объеме для реальных систем эта задача очень сложная . Рассмотрим очень простой пример, из которого можно получить представление об одном из подходов к решению задачи оптимального планирования.

Пример. Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 штук изделий . Рабочий день в кондитерском цехе длится 8 часов . Производство пирожных более трудоемко, поэтому если выпускать только их, за день можно произвести не более 250 штук , пирожков же можно произвести 1000 штук (если при этом не выпускать пирожных) . Стоимость пирожного вдвое выше , чем стоимость пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку кондитерского цеха.

Плановыми показателями являются:

- х - дневной план выпуска пирожков;

- у - дневной план выпуска пирожных.

Что в этом примере можно назвать ресурсами производства? Из того , о чем говорится в условии задачи, это :

- длительность рабочего дня - 8 часов;

- вместимость складского помещения - 700 мест .

Предполагается для простоты, что другие ресурсы (сырье, электроэнергия и пр . ) не ограничены. Формализацию цели (достижение максимальной выручки цеха) мы обсудим позже.

Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада, т. е. суммарного числа изделий.

Из постановки задачи следует, что на изготовление одного пирожного затрачивается в 4 раза больше времени, чем на выпечку одного пирожка. Если обозначить время изготовления пирожка как t мин, то время изготовления пирожного будет равно 4t мин .

Значит , суммарное время на изготовление х пирожков и у пирожных равно

tx + 4ty = (х + 4y)t.

Но это время не может быть больше длительности рабочего дня. Отсюда следует неравенство :

(х + 4y)t ≤ 8 · 60,

или

(х + 4y)t ≤ 480 .

Легко посчитать t - время изготовления одного пирожка. Поскольку за рабочий день их может быть изготовлено 1000 штук , на один пирожок тратится 480/ 1000 = 0,48 мин . Подставляя это значение в неравенство , получим :

(х + 4у) · 0,48 ≤ 480.

Отсюда

х + 4у ≤ 1000.

Ограничение н а общее число изделий дает совершенно очевидное неравенство:

х + у ≤ 700.

К двум полученным неравенствам следует добавить условия положительности значений величин х и у (не может быть отрицательного числа пирожков и пирожных). В итоге получим систему неравенств:

х + 4у ≤ 1000;

х + у ≤ 700; (1)

х ≥ 0;

у ≥ 0.

А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка - это стоимость всей проданной продукции. Пусть цена одного пирожка - r рублей. По условию задачи, цена пирожного в два раза больше, т.е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна

rx + 2ry = r(x + 2у).

Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:

F(x, у) = r(x + 2у) .

Она называется целевой функцией.

Поскольку значение r - константа, максимальное значение F(x,у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять

f(x, у) = х + 2у. (2)

Следовательно , получение оптимального плана свелось к следующей математической задаче:

Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств (1) и придающих максимальное значение целевой функции (2).

Итак, математическая модель задачи оптимального планирования для школьного кондитерского цеха построена.

Теперь следующий вопрос: как решить эту задачу? Вы уже догадываетесь, что решать ее за нас будет компьютер с помощью табличного процессора Excel. А мы обсудим лишь подход к решению, не вникая в подробности метода .

Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием.А поскольку в целевую функцию f(x, у) величины х и у входят

линейно (т.е. в первой степени), наша задача относится к разделу этой науки, который называется линейным программированием.

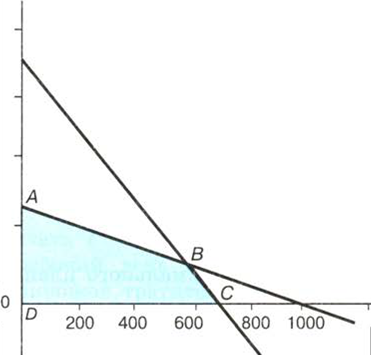
Система написанных выше неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми, соответствующими линейным уравнениям:

х + 4у = 1000,

х + у = 700,

х = 0 (ось У),

у = 0 (ось Х) .

На рис. 1 эта область представляет собой четырехугольник ABCD. Любая точка четырехугольника является решением системы неравенств (1) . Например, х = 200, у = 100. Этой точке соответствует значение целевой функции f(200, 100) = 400. А другой точке (х = 600, у = 50) соответствует f(600, 50) = 700 . Но, очевидно, искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования.

В математическом арсенале Excel имеется средство Поиск решения, с помощью которого можно решить данную задачу.

В результате решения задачи получается следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют координатам точки В на рис . 1. В этой точке значение целевой функции f(600,100) = 800. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.

800

600

400

200

Рис. 1. Область поиска оптимального плана

Система основных понятий

12 Следующая ⇒