Группа23 информатика. Тема: Модели статистического прогнозирования.. Ход урока. I. Организационный момент.. II. Актуализация знаний.. Модели

13.10.2021

Группа23 информатика

Тема: Модели статистического прогнозирования.

Цели урока:

· образовательная: ввести понятие статистических регрессионных моделей, тренда, научить строить регрессионные модели в среде ТП Excel.

· развивающая: расширить кругозор, учить применять знания в исследовательской и творческой деятельности.

· воспитательная: воспитывать активность в решении творческих задач, отстаивание собственного суждения, мнения.

Оборудование: мультимедийный проектор, ПК с установленной программой Excel.

Ход урока

I. Организационный момент.

Сегодня я хочу предложить вам поговорить о моделировании, вспомнить понятие информационной модели и изучить новый вид моделей: это – регрессионные статистические модели.

II. Актуализация знаний.

Давайте дадим общее определение модели.

Модель – это упрощенное подобие реального объекта.

Как можно классифицировать модели?

Посмотрим одну из классификаций:

Модели

Натурные или материальные – передают свойства и признаки объекта с целью:

а) создания чувственного образа (игрушка);

б) проведения с этой моделью каких-либо физических действий, испытаний (эталонная пара обуви).

2) Информационные – призваны воздействовать на мышление, т.е. на абстрактное восприятие. В них передается информация о существенных свойствах и признаках объекта.

3) Идеальные – складываются в сознании каждого конкретного человека. Эти модели субъективны – индивидуальное представление геометрической точки, идеального газа, бесконечности может значительно отличаться у разных людей.

Задание: Определите, какие из следующих моделей являются информационными.

(Демонстрируется слайд презентации. Приложение 1)

· Математические формулы

· Уравнения химических реакций

· Манекен

· Компьютерная программа

· Программа телевидения

· Авиамодель

· Оглавление книги

· Игрушечные часы

· Эталон килограмма

· Блок-схема алгоритма

Информационные модели необходимы для “наведения мостов” между внутренними представлениями разных людей, обмена знаний между ними. Использование общего языка (разговорного, математического и пр.) при построении информационной модели делает ее объективно существующей. Ее можно изучать, передавать, хранить и т.д.

Какие бывают информационные модели?

· вербальные (словесные)

· табличные

· графические

· математические (аналитические)

(Демонстрируется слайд презентации.

Давайте попытаемся смоделировать путь свободно падающего тела (без начальной скорости).

Вам вспомнилась формула: S=gt²/2. Это математическая модель. Используя эту формулу, мы можем построить таблицу, в которой отобразим зависимость переменной S от t. Это будет табличная модель. Также можно построить графическую модель свободно падающего тела. (Демонстрируется слайд из презентации.

Все это мы смогли сделать, потому что из курса физики нам известна зависимость S от t для свободно падающего тела. Но, если обратиться к истории, то станет ясно, что человек не всегда обладал знаниями об этой информационной модели.

Кем же было исследовано свободное падение тел?

Существует легенда о том, что, изучая свободное падение тел, Галилео Галилей отпускал разные шары с высокой наклонной башни в г. Пиза. Наблюдая за их падением и выполняя при этом необходимые измерения, Галилео Галилей установил законы падения тел. (Демонстрируется слайд из презентации.

Данные измерений, полученные Галилеем, носили массовый характер, т.е. их было достаточно много. В дальнейшем они были обобщены и проанализированы. Таким образом собранные данные называются статистическими.

Существует специальная наука статистика.

Статистика – это наука о сборе, измерении и анализе массовых количественных данных.

Статистические данные:

· всегда являются приближенными, усредненными, носят оценочный характер, однако, они верно отражают характер зависимости величин.

· для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.

Статистика опирается на сложные математические методы и расчеты, но в арсенале ТП Excel заложены возможности использования этих методов.

Рассмотрим пример: Наиболее сильное влияние на рост заболеваемости бронхиальной астмой производит угарный газ.

Цель: выявить эту зависимость.

Действия:

Подготовительный этап: собираем данные из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (количество больных на тысячу человек).

Этап моделирования:

1. строим таблицу.

2. строим точечную диаграмму по данным таблицы. (Рисунок 2.)

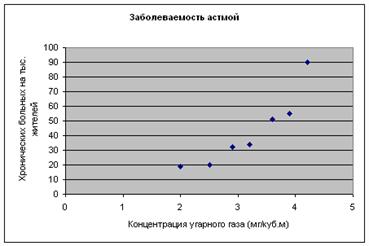
Рисунок 2

подбираем функцию, график которой пройдет как можно ближе к экспериментальным точкам.

Строить функцию так, чтобы график точно проходил через все точки, не имеет смысла, т.к.:

· функция примет довольно сложный вид

· собранные нами данные носят приближенный характер

Основные требования к функции:

· функция должна иметь простой вид

· отклонения графика функции от экспериментальных точек должны быть минимальны.

Один из методов подбора такой функции и вычисления ее параметров был предложен в XVIII веке немецким математиком Карлом Гауссом. Он называется метод наименьших квадратов. Как и все методы математической статистики он не является простым для исполнения.

(Демонстрируется слайд из презентации.

Полученную функцию, график которой приведен на рис. 3, называют регрессионной моделью.

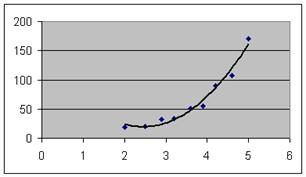
Рисунок 3

Область определения данной функции – концентрация угарного газа в атмосфере.

График регрессионной модели называется трендом.

Trend (англ.) – общее направление, тенденция.

Чтобы можно было определить, насколько удачной будет регрессионная модель, вводится величина R²: коэффициент достоверной аппроксимации.

0< R²<1. R²должен стремиться к 1 для удачно подобранной функции.

4. копируем точечную диаграмму три раза.

У нас получилось четыре заготовки с изображением точечной диаграммы зависимости уровня заболеваемости от концентрации угарного газа в атмосфере.

· Далее выполняем следующие действия:

· щелкнуть левой кнопкой мыши по полю диаграммы;

· выполнить команду => Диаграмма => Добавить линию тренда;

· в открывшемся окне на закладке “Тип” выбрать “Линейный тренд”;

· перейти к закладке “Параметры”; установить галочки на флажках “показывать уравнения на диаграмме” и “поместить на диаграмму величину достоверной аппроксимации R^2”, щелкнуть по кнопке ОК.

Диаграмма готова. Смотри приложение 2.

Аналогично получаем другие типы трендов: экспоненциальный и квадратичный (полиномиальный тип функции с указанием степени 2)

R²ближе всего к 1 у квадратичной модели. Значит, она самая удачная. А самая неудачная – линейная модель.

Для чего же нам нужно выявлять эти зависимости (создавать модели)?

1. для объяснения явлений и процессов.

2. для прогнозирования процессов.

3. для управления процессами.

4. мы будем прогнозировать по модели.

Прогноз бывает двух видов:

1. восстановление значения внутри области экспериментальных данных (интерполяция)

2. продолжение линии тренда за границы экспериментальных данных (экстраполяция)

На четвертой диаграмме прогнозируем на 2 единицы вперед.

· на вкладке “Параметры” в области “Прогноз” в строке “вперед на” установить 2 единицы.

Далее в таблице исходных данных тоже попытается осуществить прогноз. Заводим данные о концентрации угарного газа: 5,5; 6; 6,5; 7; 7,5; 8; 8,5; 9 мг/куб.м, и для г. Калуги 3 мг/куб.м. В область значений заводим регрессионную модель (математическую функцию y=21,845x²-106,97x+150,21)

С экстраполяцией надо быть осторожными, т.к. применимость любой регрессионной модели ограничена, особенно, за пределами экспериментальной области.

Например, если С=9 мг/куб.м., то Р приблизительно равно 1000 больных.

В таких крайних случаях система находится в неравновесной, неопределенной ситуации. Точки, вблизи которых резко усиливается хаотическое развитие системы, называются точками бифуркации. Модель перестает быть адекватной ситуации. Нужны новые экспериментальные данные и, возможно, новая модель.

IV. Использование полученных знаний в других ситуациях.

Давайте обратимся еще к одному примеру: проследим рост численности населения Земли. (демонстрируется слайд презентации)

При анализе данной модели наглядно видно, что ветвь графика уходит в бесконечность между 2010 и 2025 годами. Как можно это интерпретировать? Очевидно, что здесь мы имеем дело с точкой бифуркации, т.е. система хаотична. По данной модели прогнозировать численность населения Земли нельзя. Можно говорить только о разного рода предсказаниях..

VI. Домашнее задание.

Составить конспект.