
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Свойства функций у=cosx, y=sinx и их графики
| Урок №11 | 02 ноября 2021г. | 11 класс. Алгебра |
| Тема урока: | ||
Свойства функций у=cosx, y=sinx и их графики
- изучение свойств функции y=cos x, y=sinx. построение графика функции, применение полученных знаний на практике.
- формирование умений построения и отображения свойств графиков функции у=cosx; y=sinx
- активизировать интерес к получению новых знаний;
- формирование точности и аккуратности при выполнении чертежей.
урок усвоения новых знаний
Рассказ учителя, самостоятельная работа, работа учащихся с учебником.
ДО, Учебник – «Алгебра и начала математического анализа» 10-11 класс, авторы Ш.А.Алимов, Ю.М.Колягин и др.М.:-Просвещение,2016
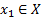 и
и 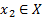 ,
, 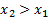 выполняется неравенство
выполняется неравенство 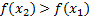 . Другими словами – большему значению аргумента соответствует большее значение функции.
Функция y=f(x) убывает на интервале X, если для любых
. Другими словами – большему значению аргумента соответствует большее значение функции.
Функция y=f(x) убывает на интервале X, если для любых 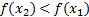 . Другими словами – большему значению аргумента соответствует меньшее значение функции.
Точку х0 называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство
. Другими словами – большему значению аргумента соответствует меньшее значение функции.
Точку х0 называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство 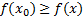 . Значение функции в точке максимума называют максимумом функции и обозначают ymax.
Точку х0 называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство
. Значение функции в точке максимума называют максимумом функции и обозначают ymax.
Точку х0 называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство 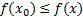 . Значение функции в точке минимума называют минимумом функции и обозначают ymin.
Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции
. Значение функции в точке минимума называют минимумом функции и обозначают ymin.
Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции 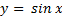 , где a≠0.
, где a≠0.