
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение
Дата:14 октября 2021г. группа: 2-СПХ-5-20
Предмет: Прикладная математика.
Преподаватель:Шкурко Лариса Александровна
Тема занятия:4-я пара: Векторы. Скалярное произведение векторов и его свойства.
Тип занятия: занятие усвоения нового материала.
Форма учебного занятия:дистанционная.
Цели занятия:
· закрепить умение находить угол между векторами;
· повторить понятие скалярного произведения и закрепить умение применять его при решении задач;
· сформулировать и доказать теорему о скалярном произведении двух векторов в координатах и ее следствия;
- познакомить учащихся со свойствами скалярного произведения векторов;
- показать применение скалярного произведения векторов в координатах при решении задач.
Использованные источники:
· Атанасян Л. С. и др. Геометрия 7–9, 10-11 классы.
· http://www.yaklass.ru/p/geometria/9-klass/sootnoshenie-mezhdu-storonami-i-uglami-treugolnika-skaliarnoe-proizvedenie_-9222/skaliarnoe-proizvedenie-vektorov
· https://interneturok.ru/geometry/9-klass/skalyarnoe-proizvedenie-vektorov/skalyarnoe-proizvedenie-v-koordinatah-svoystvo-skalyarnogo-proizvedeniya
Лекционный материал
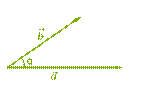 Вспомним: очень важно правильно определить угол между векторами. Если векторы не имеют общей начальной точки, необходимо представить, какой угол бы образовался, если их переместить к общей начальной точке.
Вспомним: очень важно правильно определить угол между векторами. Если векторы не имеют общей начальной точки, необходимо представить, какой угол бы образовался, если их переместить к общей начальной точке.
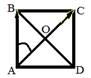
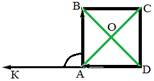
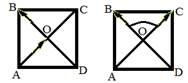
Вспомним свойства квадрата:
1. Все углы квадрата прямые.
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
 а) а)
| У векторов АВ и АС общее начало, значит  =45°. =45°.
|
 б) б)
| Вектор DA переместим в общую начальную точку А, получится вектор АК. Тогда 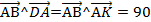 °. °.
|
 в) в)
| У векторов ОА и ОВ общее начало, значит 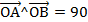 °. °.
|
 г) г)
| Вектор АО переместим в общую точку О, получится вектор ОС. Тогда 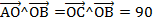 °. °.
|
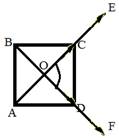
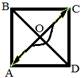 д) д)
| У векторов ОА и ОС общее начало – точка О. Значит  °. °.
|
 е) е)
| Переместим векторы АС и BD в общую начальную точку О.
Тогда  °. °.
|
 ж) ж)
| Переместим вектор DB в общую точку А, получится вектор АМ. Тогда 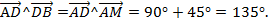
|
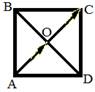 з) з)
| Векторы АО и ОС - сонаправленные. Значит 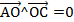 °. °.
|
Определение
| Скалярным произведением двух векторов a⃗ и b⃗ называется произведение их длин (модулей этих векторов) на косинус угла между ними: a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cosα. |
Свойства скалярного произведения векторов:
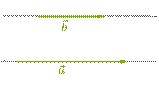
1. Если векторы сонаправлены, то a⃗ˆb⃗ =0°:
| Так как косинус угла в 0° равен 1, то скалярное произведение сонаправленных векторов является произведением их длин: a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 0°=|a⃗|⋅|b⃗|⋅1=|a⃗|⋅|b⃗|. |
| Если два вектора равны, то такое скалярное произведение называют скалярным квадратом: a⃗⋅a⃗ =|a⃗|⋅| a⃗|⋅cos 0°=|a⃗|⋅| a⃗|⋅1=|a⃗|2= a⃗2. |
2. Если векторы противоположно направлены, то a⃗ˆb⃗ =180°:
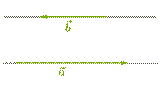 Так как косинус угла в 180° равен (-1), то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин:
a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 180°=|a⃗|⋅|b⃗|⋅(-1) = - |a⃗|⋅|b⃗|. Так как косинус угла в 180° равен (-1), то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин:
a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 180°=|a⃗|⋅|b⃗|⋅(-1) = - |a⃗|⋅|b⃗|.
|
3. Векторы называют перпендикулярными, если a⃗ˆb⃗ =90°:
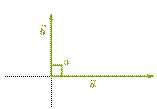 Так как косинус угла в 90° равен 0, то скалярное произведение перпендикулярных векторов равно 0: a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 90°=0. Так как косинус угла в 90° равен 0, то скалярное произведение перпендикулярных векторов равно 0: a⃗⋅b⃗ =|a⃗|⋅|b⃗|⋅cos 90°=0.
|
4. Внимательно рассматриваются ситуации, когда векторы образуют тупой угол:
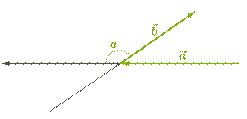
| 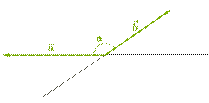
| Так как косинус тупого угла отрицательный, то скалярное произведение таких векторов, которые образуют тупой угол, является отрицательным. |
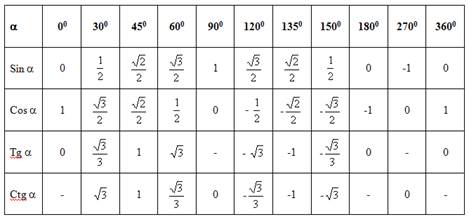
Таблица значений синуса, косинуса, тангенса и котангенса некоторых углов
Теорема. Скалярное произведение векторов 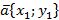 и
и 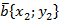 выражается формулой
выражается формулой
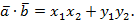
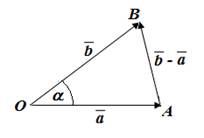
Доказательство.
1. При 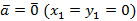 или
или 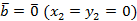 теорема очевидна.
теорема очевидна.
2. Пусть  и
и 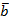 – ненулевые векторы. Тогда по теореме косинусов
– ненулевые векторы. Тогда по теореме косинусов
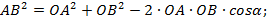
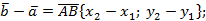
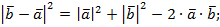
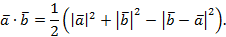
Перейдем в этой формуле к координатам.
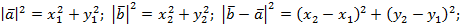
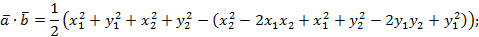
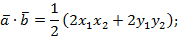
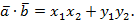
Уточним, что теорема доказана для случая неколлинеарных векторов, в доказательстве был использован треугольник, теорема косинусов, поэтому случай коллинеарных векторов тоже рассмотрим, при этом учтем, что угол между коллинеарными векторами может быть равен 180° или 0°.
3. Пусть 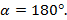
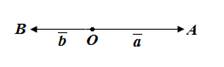
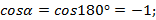
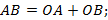
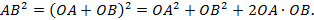
Подгоним это равенство под формулу, полученную при доказательстве теоремы.
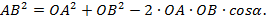
Формула та же самая, если записать ее в координатах, то получим
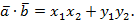
4. Аналогично рассмотрим случай 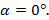
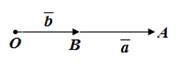
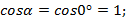
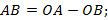
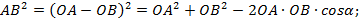
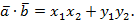
Вывод: 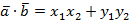 для всех векторов
для всех векторов  и
и 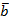 .
.
2) Следствия из теоремы
Сформулируем следствия из доказанной теоремы.
Следствие 1. Ненулевые векторы  и
и 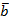 перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда 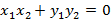 .
.
Действительно, 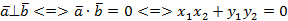 .
.
Следствие 2. Косинус угла между ненулевыми векторами  и
и 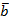 выражается формулой:
выражается формулой:
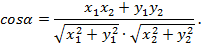
Действительно, 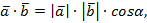
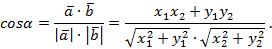
3) Свойства скалярного произведения векторов
Рассмотрим свойства скалярного произведения векторов.
Для любых векторов 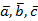 и любого числа k справедливы соотношения:
и любого числа k справедливы соотношения:
1. 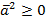 , причем
, причем 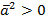 при
при 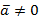 .
.
Доказательство.
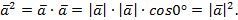
Но 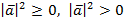 при
при 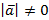 .
.
2. 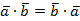 (переместительный закон).
(переместительный закон).
Доказательство (из определения).

3. 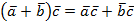 (распределительный закон).
(распределительный закон).
Доказательство.
Для доказательства используем метод координат.
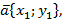
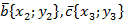 , тогда
, тогда
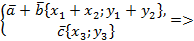
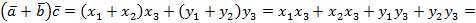
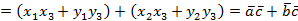 .
.
4. 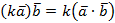 (сочетательный закон).
(сочетательный закон).
Доказательство.
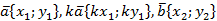 , значит,
, значит,
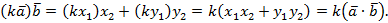
Замечание. Распределительный закон справедлив и в случае нескольких слагаемых, например,
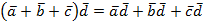 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|