МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №91 С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ОТДЕЛЬНЫХ ПРЕДМЕТОВ

ЛЕНИНСКОГО РАЙОНА ГОРОДА НИЖНЕГО НОВГОРОДА

Научное общество учащихся

ПРИЛОЖЕНИЯ ТЕОРЕМЫ ПИФАГОРА

Работу выполнил:

ученик 9 Г1 класса

Манкеров Александр Сергеевич

Руководитель:

Ларькина Галина Александровна

Учитель математики

Нижний Новгород

Пифагор VI в. до н.э.

Содержание.

Введение	Стр.

Глава I. Пифагор и его теорема.
1.1 Краткая биография Пифагора.
1.2 О теореме Пифагора, ее истории и доказательствах.

Глава II. Приложения теоремы Пифагора.
2.1 Теорема о гиппократовых луночках.
2.2. Теорема о сумме квадратов диагоналей параллелограмма.
2.3 Длина медианы треугольника.
2.4 Решение задач.

Заключение.
Список литературы.
Приложения.

Введение.

Пребудет вечной истина, как скоро

Ее познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принес в жертву быка». Сегодня теорема Пифагора обнаружена в различных частных задачах и чертежах: и в египетском треугольнике в папирусе времен фараона Аменемхета I (ок. 2000 до н.э.), и в древнейшем китайском трактате «Чжоу-би суань цзинь» («Математический трактат о гномоне»), время создания которого точно не известно, но где утверждается, что в XII в. до н.э. китайцы знали свойства египетского треугольника, а к VI в. до н.э.— и общий вид теоремы, и в древнеиндийском геометрическо-теологическом трактате VII — V вв. до н.э. «Сульва сутра» («Правила веревки»),— несмотря на все это, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадется.

Теорема Пифагора является одной из главных теорем геометрии, её изюминкой, но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных применений.

Интересна для изучения именно эта тема, так как многие слышали о теореме Пифагора, но немногие знают об интересных и полезных приложениях основанных на ней. Поэтому цель моей работы – показать именно приложения и различные применения теоремы Пифагора.

В первой части моей работы рассмотрен исторический материал, связанный с именем Пифагора, а также рассмотрены некоторые способы ее доказательства, интересна история самой теоремы. Во второй главе будут приведены примеры приложений и применений теоремы Пифагора, решены интересные задачи практического содержания.

Глава I. Пифагор и его теорема.

1.1. Краткая биография Пифагора

О жизни Пифагора известно немного. Он родился в 580 г . до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.

Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.

Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки.

Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги — в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки.

Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду.

Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне умели решать линейные, квадратные и некоторые виды кубических уравнений.

Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В одной из греческих колоний Южной Италии, в городе Кротоне, Пифагор основал свою школу.

Школа Пифагора являлась тайным союзом молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками.

Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:

• теорема о сумме внутренних углов треугольника;

• построение правильных многоугольников и деление плоскости на некоторые из них;

• геометрические способы решения квадратных уравнений;

• деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;

• доказательство того, что 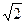не является рациональным числом;

• создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.

Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.

Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания.

После его смерти ученики окружили имя своего учителя множеством легенд.

Союз пифагорейцев был тайным. Эмблемой или опознавательным знаком союза являлась пентаграмма — пятиконечная звезда. Пентаграмме присваивалась способность защищать человека от злых духов.

У немецкого поэта Гёте в трагедии «Фауст» описывается случай, когда дьявол Мефистофель проник в жилище учёного Фауста, потому что пентаграмма на его доме была плохо начерчена, и промежуток в уголке остался (см. рис. 1).

Рис.1

Мефистофель: Нет, трудновато выйти мне теперь. Тут кое-что мешает мне немного: Волшебный знаку вашего порога.

Фауст: Не пентаграмма ль этому виной? Но как же, бес, пробрался ты за мной? Каким путем впросак попался?

Мефистофель: Изволили ее вы плохо начертить, И промежуток в уголку остался, Там, у дверей, -и я свободно мог вскочить.

Этот пятиугольник обладает интересным геометрическим свойством: поворотной симметрией пятого порядка, т.е. имеет пять осей симметрии, которые совмещаются при каждом повороте на 72 градуса. Именно этот тип симметрии наиболее распространён в живой природе: у цветков незабудки, гвоздики, колокольчика, шиповника, лапчатки гусиной, вишни (см. рис.2), груши, яблони, малины, рябины и т.д. Поворотная симметрия пятого порядка встречается и в животном мире, например, у морской звезды (см. рис.3) и панциря морского ежа.

Рис.2

Рис.3

1.2. О теореме Пифагора, ее истории и доказательствах.

Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.

Предполагают, что во времена Пифагора теорема звучала не так как сегодня, а именно:

«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».

Рис.5

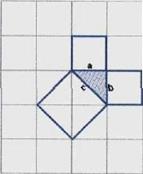Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников (см.рис.5). Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

Учащиеся средних веков при изучении теоремы придумывали стишки, рисовали шаржи (см.рис.6,7,8), например, такие:

1. стихи - «Пифагоровы штаны во все стороны равны».

2. шаржи —

Рис.8

Рис.6

Рис.7.

Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. На протяжении последующих веков были найдены другие доказательства теоремы Пифагора. В настоящее время их насчитывается более 500 (геометрических, алгебраических, механических и т.д.) и общепринятая формулировка теоремы такова: «Впрямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

Глава II. Приложения теоремы Пифагора/

Всего известно около 500 различных доказательств теоремы Пифагора. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности и свидетельствует о её широком применении. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана.

На сегодняшний день существует несколько интересных приложений теоремы Пифагора, которые встречаются во многих учебниках геометрии.

2.1 Теорема о гиппократовых луночках.

Рис.9.

Предложение в том виде, в каком оно будет здесь сформулировано, не встречается у самого Гиппократа, который   нашёл квадратуру только для некоторых луночек Данную теорему доказал араб Ибн Альхаитам, французские математики А. де Лион и Г. Парди высказали её вновь в 1654 и в 1671 гг.

Теорема: Если на гипотенузе прямоугольного треугольника как на диаметре описать полуокружность, лежащую с той же стороны гипотенузы, что и сам треугольник, то площадь полукруга, построенного на гипотенузе, будет равна сумме площадей полукругов, построенных на катетах этого прямоугольного треугольника (см. рис. 9).

Дано: прямоугольный треугольник; полуокружность

Доказать: вершина треугольника принадлежит полуокружности

Доказательство:

1)Пусть Sа, Sb и Sс - площади полукругов, построенных на катетах и гипотенузе.

2)Согласно следующей теореме о подобных фигурах, построенных на сторонах прямоугольного треугольника: «Если на катетах и на гипотенузе прямоугольного треугольника построены какие угодно подобные между собой фигуры Sа, Sb, Sс, так, что катеты и гипотенуза являются сходственными отрезками этих фигур, то имеет место равенство»:

Sа + Sb = Sс.

3)Этот же результат можно получить, умножив обе части равенства:

с²= а²+ b²на π/8. В самом деле, равенство

π*с/8 = π*а/8 + π*b/8

означает, что площадь полукруга с диаметром с равна сумме площадей двух других полукругов, с диаметрами а и b.

Если мы отнимем одни и те же части (на рисунке они не закрашены) как от полукруга, построенного на гипотенузе, так и от полукругов построенных на катетах, то, вследствие только что доказанной теоремы, получим, что сумма площадей луночек равна площади треугольника.

2.2. Теорема о сумме квадратов диагоналей параллелограмма.

Дано: параллелограмм АВСD со сторонами а,b и диагоналями с,d. рис. 10). Доказать: с² + d² = 2а²+ 2b²

    B1

Рис.10

В b             D C1

Доказательство:

1. Построим высоты: ВВ1,СС1 и рассмотрим треугольник ВB1D, тогда по теореме Пифагора: ВВ1²+В1D²= с²= (а²- АВ1²)+ (b-АВ1)²=

= а²- АВ1²+ b²- 2bАВ1+АЙ1² = а²+b²-2bАВ1.

2. Рассмотрим треугольник АСС1, тогда по теореме Пифагора: СС1² +АС1²= =d² =(а² – DC1²) + (b + DC1)² = а² – DC1² + b² + 2bDC1 +DС1²= a² + b² + 2bDC1

3. с² + d² = а²+b²– 2bАВ1+ а²+b²+2bDС1= 2а²+2b²– 2bAВ1+2bAВ1=2а²+2b²,

что и требовалось доказать.

2.3. Длина медианы треугольника.

Дано: треугольник АВС со сторонами а,b,n и медианой m (см. рис. 11).

Доказать: m² = ¼ ( 2а²+ 2b²- n²)

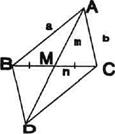
Доказательство:

Достроим треугольник АВС до параллелограмма АВСD, на основании равенства параллелограмма

Рис.11.

4m² + n² = 2а² + 2b²→ m² =1/4 (2а² + 2b² - n²),

что и требовалось доказать.

2.4 Решение задач.

Рассмотрим применение теоремы Пифагора в школьном курсе геометрии. Воспользуемся, прежде всего, возможностями, которые даёт теорема Пифагора для вычисления длин отрезков некоторых известных нам фигур:

Задача 1:

                   Дано: Треугольник ВСЕ - прямоугольный с гипотенузой DE (см. рис. 12)

                       Решение:

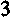
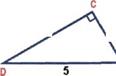                             по теореме Пифагора:

DЕ² = DC² + СЕ², DС² = DЕ² - СЕ², DС² =52 - 32, ВС² = 25-9,
В         DС² = 16,

Рис.12



                    Ответ: DC = 4

Получили прямоугольный треугольник со сторонами 3, 4, и 5 ед. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, т.к. он был известен ещё древним египтянам. Они использовали этот треугольник в «правиле верёвки» для построения прямых углов при закладке зданий, храмов и алтарей.

Задача 2:

Дано:

Из одного порта вышли два корабля: один – на восток, другой – на север.

Расстояние от главного порта до порта на востоке – 300 миль, а до порта на севере – 400 миль. Каково расстояние между двумя портами?

Решение 1:

Угол между курсами кораблей будет составлять 90 , отрезок, соединяющий порты назначения является гипотенузой (х) треугольника, вершинами которого являются порты назначения и главный порт. Следовательно, из условия задачи нам известны длины катетов прямоугольного треугольника.

По теореме Пифагора:

х = 300 + 400 = 250000,

х = ,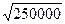

х = 500.

Ответ: 500 миль от восточного порта до северного.

Решение 2:

Используя понятие египетского треугольника ( стороны которого равны 3,4 и 5) мы можем решить эту задачу, не проводя вычислений, т.е. гипотенуза прямоугольного треугольника равна 500 миль.

Ответ: 500 миль от восточного порта до северного.

Задача 3:

Какую наибольшую высоту должна иметь телевизионная вышка, чтобы передачу можно было осуществить в радиусе R=200 км? ( R Земли =6380 км).

Рис. 13

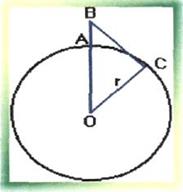Решение:

Пусть АВ= х, ВС=R=200 км, ОС= r =6380 км, ОВ = OА+АВ,

ОВ = r + х, ВС является касательной к окружности в точке С, значит угол ОСВ = 90 , следовательно треугольник ОСВ прямоугольный, где ОВ - гипотенуза.

Используя теорему Пифагора, получим:

X=√ (r²+R²) - r = 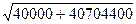- 6380 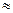6383,13 – 6380 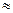3,13 км

Ответ: телевизионная вышка должна иметь высоту не менее чем 3,13 км.

Задача 4:

Дано:

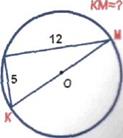
Угол КLМ вписан в окружность и опирается на диаметр КМ, КL=5, LМ=12, найти диаметр окружности (см. рис.14).

Решение:

Так как вписанные углы, опирающиеся на диаметр, - прямые, то угол КLМ - прямой. Значит, треугольник КLМ - прямоугольный.

Рис.14.





По теореме Пифагора для прямоугольного треугольника КLМ с гипотенузой КМ:

КМ² = КL² + LМ²= 5² + 12²=169,

КМ=√169 = 13.

Рис.15

Ответ: диаметр окружности равен 13
Задача 5: (из китайской «Математики в девяти книгах» )

Дано:

«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу,      то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?»(см. рис. 15).

       Решение:

1. Пусть глубина водоёма равна х, согласно условиям задачи расстояние от камыша до берега равна половине ширины водоема, т.е. 5 чи. Треугольник, образованный камышом, растущим со дна и наклонённым к берегу, и поверхностью водоёма, является прямоугольным, в котором поверхность водоёма (5 чи) и растущий камыш (х чи) являются катетами, а наклонённый камыш((х+1) чи) является

гипотенузой данного треугольника.

2.Согласно теореме Пифагора,

    (х+1)² = х² +5² ,

х²+2х+1-х²= 25,

2х = 24,

x=12

3. Глубина водоёма составляет 12 чи, а длина камыша равна глубина водоёма + 1=13 чи.

Ответ: Глубина водоёма равна 12 чи, а длина камыша – 13 чи.

Задача 6:

Дано:

Рис.16

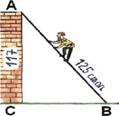
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготъю 125 стоп. И ведати хочет, колико стоп сея лестницы пилений конец от стены отстояти имать» (см. рис.16).

Решение:

1. Обозначим основание стены – С , соединение лестницы со стеной – А, а основание лестницы – В, в результате получили треугольник АВС, в котором угол ВСА прямой.
Согласно условию задачи катет АС=117(стоп), гипотенуза АВ=125(стоп).

2. Согласно теореме Пифагора АВ² = АС² + СВ² ,

СВ²= АВ²- АС²= 125²-117²= 1936,

СВ = 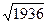  = 44( стопы)

Ответ: основание лестницы надо расположить на 44 стопы от стены.
Задача 7 : (индийского математика ХII века Бхаскары) (Рис. 17)

Дано:

Рис.17

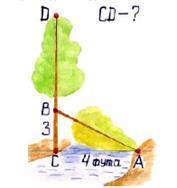
«На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?» (см.рис.17)

Решение:

1. Обозначим основание тополя – С, соединение вершины тополя с противоположным берегом реки –А, точку надлома тополя – В, а вершину тополя – D, в результате получили треугольник АВС, в котором угол ВСА прямой. Согласно условию задачи катет АС = 4(фута), катет СВ = 3(фута).

2.Согласно теореме Пифагора АВ²= АС² +СВ²,

АВ²= СВ² +АС² = 3²+4² = 25,

                                     АВ = √25 = 5 ( футов)

3.Высота всего тополя равна CD = CB + BD, т.к. BD = АВ = 5 футов, то СD = 3+5 = = 8 (футов).

Примечание: используя понятие египетского треугольника решение данной задачи может быть следующим: т.к. треугольник АВС прямоугольный и катеты равны 3,4 футам, то гипотенуза равна 5 футам, высота тополя соответственно равна 8 футам.

Ответ: высота тополя составляет 8 футов.

3аключение.

В заключении данной работы можно сделать следующий вывод : невозможно глубоко познать такую науку как математика (алгебра, геометрия и т.п.) без подробного изучения истории данной науки, ее выдающихся личностей-ученых, философов, путешественников.

Только владея знаниями исторического развития науки можно участвовать в продвижении и углублении данной науки в дальнейшем, к чему и стремятся не только представители ученого мира, но и все человечество.

В настоящем реферате рассмотрены приложения теоремы Пифагора, приведены некоторые иллюстрации к доказательствам теоремы Пифагора, некоторые задачи практического содержания. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для закрепления знаний по теме.
     Работа над рефератом потребовала изучения большого количества литературы (мной изучены: научные статьи, различная учебная и справочная литература по геометрии и истории математики)., позволила научиться решать практические задачи.

Основной частью данной работы является раздел, посвященный приложению теоремы Пифагора, где повествуется о применении теоремы, как в геометрии, так и на практике, и других науках сегодня и в древние времена, а так же о теоремах, основанных на теореме Пифагора. В данной научной работе изложены как формулировки задач и теорем, так и их подробные решения и доказательства с применением наглядной демонстрации. Таким образом, цель работы рассмотреть приложения теоремы Пифагора достигнута.

В дополнение к вышесказанному хотелось бы отметить, что приведенная информация в реферате - лишь малая часть того, что можно рассказать об этой уникальной теореме и есть еще много интересных аспектов, исторических фактов, задач и научных споров, связанных с именем Пифагора и его достижениями, что еще раз подтверждает, что теорема Пифагора как была актуальна в древние времена, так и сегодня не дает покоя умам ученого мира.

Список литературы.

1. Акимова С. Занимательная математика, серия «Нескучный учебник». - Санкт-Петербург.: «Тритон», 1997.

2. Бронштейн И.Н., К. А. Семендяев. Справочник по математике для инженеров и учащихся ВУЗов, Москва «Наука», 1980г.

3. Геометрия, 7-9: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, СБ. Кадомцев и др. - 14-е изд. - М.: Просвещение, 2004г.

4. Глейзер Г.И. История математики в школе. - М.: Просвещение, 1981.

5. Еленьский Ш. По следам Пифагора. М., 1961.

6. Иген В., Чемпион Н., Детская энциклопедия, Москва, ОНИКС 21 век, 2001г.

7. Погорелов А.В. Геометрия: Учеб. для 7 - 11 кл. общеобразоват. учреждений. - 5-е изд.- М.: Просвещение, 1995.

8. Ресурсы Интернет: www.Math.ru

9. Чистяков В.Д. Старинные задачи по элементарной математике. Минск, 1978.

10. Энциклопедический словарь юного математика / Сост. А.П. Савин. - 3-е изд., испр. и доп. - М.: Педагогика-Пресс, 1997.

11. Я познаю мир: Детская энциклопедия: Математика. — М, 1997.