Сфера и шар. Площадь сферы. Уравнение сферы. Взаимное расположение сферы и плоскости

Сфера и шар

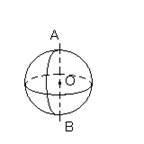Сферойназывается поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (центра сферы). Данное расстояние называется радиусом сферы R. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Диаметр сферы равен 2R.

Тело, ограниченное сферой, называется шаром.

Центр, радиус и диаметр сферы называется также

центром, радиусом и диаметром шара.

Площадь сферы

R – радиус сферы

Уравнение сферы

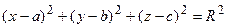
Если центр сферы находится в точке А(a, b, c),

а радиус сферы R, тогда уравнение сферы имеет вид:

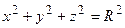Если центром сферы является начало координат,

то уравнение имеет вид:

Линия пересечения двух сфер есть окружность.

Взаимное расположение сферы и плоскости

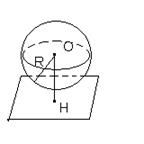
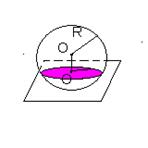R – радиус сферы; d – расстояние от центра сферы до плоскости α.

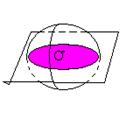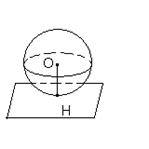
1. d < R OO₁ = d	2. d = 0	3. OH ┴ α d = \| OH \| d > R
Сечение сферы плоскостью есть окружность		Сфера и плоскость не имеют общих точек
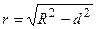
r – радиус сечения	Радиус сечения равен радиусу сферы R.
4. OH ┴ α \| OH \| = d d = R	Сфера и плоскость α имеют только одну общую точку. Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка (Н) называется точкой касания плоскости и сферы. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.