Лабораторная работа №1

Минобрнауки России

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Юго-Западный государственный университет»

(ЮЗГУ)

Кафедра теоретической механики и мехатроники

Лабораторная работа №1

По дисциплине: «Компьютерное управление мехатронными системами»

На тему: «Дискретизация и квантование непрерывных сигналов»

В-III

Выполнил: ст. гр. МТ-91 Яковлев И.А.

Проверил: к.т.н., ст. преподаватель

Яцун А.С.

Курск, 2013 г.

Цель работы:исследование влияние частоты дискретизации на точность восстановленных сигналов. Исследование эффекта поглощения частот.

Выполнение работы:

Заданная функция: y(t)=cos(0.5t)+sin(0.08t)

График приведённой функции представлен на рисунке 1:

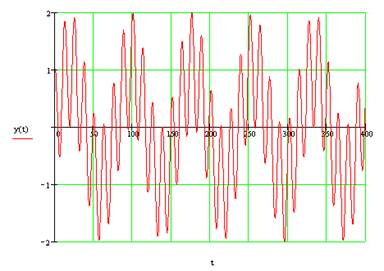
Рис.1 График зависимости функции y(t)=cos(0.5t)+sin(0.08t) от времени t

Выберем время квантования сигнала T=5 c. Полученные дискретные отсчёты (рисунок 2) соединим прямыми:

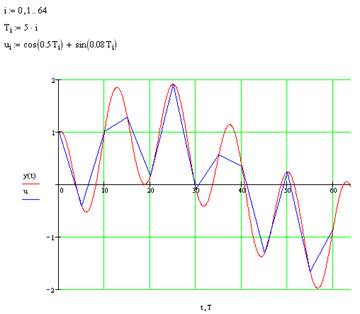
Рис.2 Графики зависимостей исходной функции y(t) и функции полученной в результате квантования u от непрерывного времени t и дискретного времени T

Применим быстрое преобразование Фурье для получения спектра частот для заданной функции (рисунок 3):

Рис.3 Частотный спектр функции y(t)=cos(0.5t)+sin(0.08t)

Вычислим максимальную частоту. В исходной функции y(t)=cos(0.5t)+sin(0.08t) наибольшую круговую частоту имеет cos(0.5t), то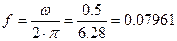

Как видно из результатов, максимальная частота приближённо совпадает с максимальной частотой спектра на рис. 3.

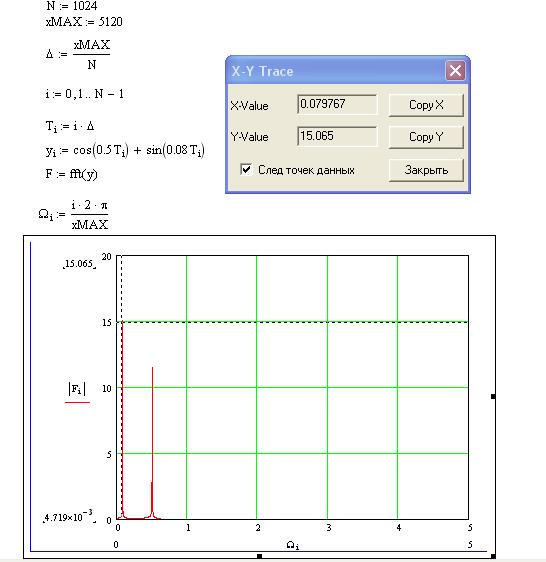
Рис.4 Частотный спектр функции y(t)=cos(0.5t)+sin(0.08t)

Согласно теореме Котельникова-Найквиста(Шеннона), частота квантования должна быть в 2 и более раз быть больше найденной т.е.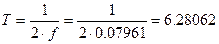

Частота квантования при этом будет равна:

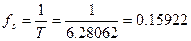
Функция cos(0.5t) находится в максимуме в нулевой момент времени, то квантование начинаем с T.

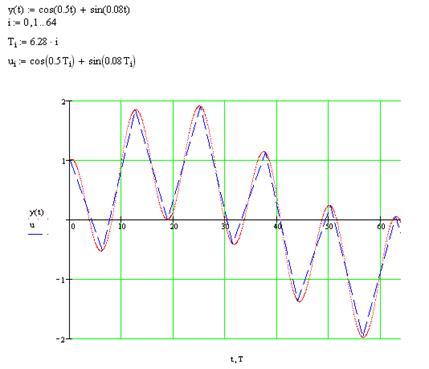
Рис.5 Графики зависимостей исходной функции y(t) и функции u, полученной в результате квантования с частотой f_s от непрерывного времени t и дискретного времени T

Если взять частоту квантования меньше, чем, частота спектра, то мы будем наблюдать так называемый эффект поглощения частот: частота квантования окажется недостаточной для качественной передачи сигнала.

При увеличении частоты квантования качество получаемого сигнала значительно увеличивается. Например для частоты квантования f=8f_s почулим следующую диаграмму (рисунок 6):

Рис.6 Графики зависимостей исходной функции y(t) и функции u, полученной в результате квантования с частотой 8*f_s от непрерывного времени t и дискретного времени T

Выводы: в ходе лабораторной работы была экспериментально проверена и доказана теорема Котельникова-Найквиста(Шеннона0 для квантования сигнала. При частоте квантования меньше, чем f_s, непрерывный сигнал квантуется некачественно (возникает эффект «поглощения частот»). При квантовании с частотой больше или равной f_s мы получаем качественный дискретный сигнал без потери информации.