
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема урока Многоугольники и их свойства
Урок 29 20.10.2021
Обратная связь:работыприсылать личным сообщением ВК
Задание:проработать конспект, изучить видеоматериал, выполнить д/з.
Тема урока Многоугольники и их свойства
Цели урока:
познакомиться с понятием и видами правильных многоугольников, с некоторыми их свойствами;научить пользоваться формулой для вычисления угла правильного многоугольника
Ход урока
Дано:
ΔABC∾ΔKMN;
AB и KM – сходственные;
BC и MN – сходственные;
АВ=4 см;
ВС=5 см;
СА=7 см;
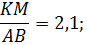 Найти:
KM; MN; KN.
Найти:
KM; MN; KN.

| Решение:
1) Сходственные стороны в подобных треугольниках лежат против равных углов.
АВ и КМ – сходственные, значит ∠С=∠N.
ВС и МN – сходственные, значит ∠А=∠К.
2)Получаем следующий чертеж
3) 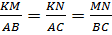 (так как ΔMNK∾ΔBCA) и (так как ΔMNK∾ΔBCA) и 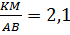 . Тогда . Тогда
|
Ответ: KN=14,7 см; KM=8,4 см; MN=10,5 см.
Новая тема
1. Как найти сумму углов правильного многоугольника (S = (n-2)180°).
2. Как найти градусную величину внутреннего угла правильного выпуклого многоугольника? ( (n-2)180°: n ).
Сторона правильного треугольника равна 4 см. Найдите радиусы вписанной и описанной окружностей.
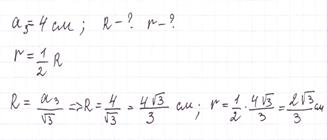
Радиус окружности, описанной около квадрата равен 4√ 3 см. Найдите сторону квадрата и радиус вписанной в него окружности.
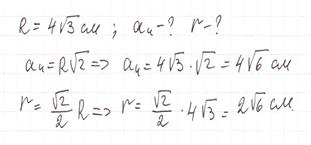
Радиус окружности, вписанной в правильный шестиугольник, равен 4√ 3 см. Найдите сторону шестиугольника и радиус описанной около него окружности.
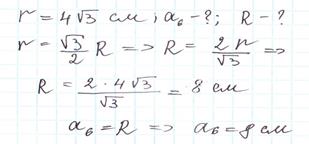
В треугольнике ABC АС = 4, ВС = 3, угол C равен 900. Найдите радиус вписанной окружности.
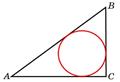
Воспользуемся формулой радиуса окружности вписанной в треугольник:
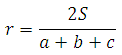
где a, b, c – стороны треугольника
S – площадь треугольника
Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.
По теореме Пифагора:
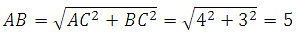
Найдём площадь:
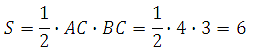
Таким образом:
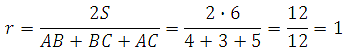
Ответ: 1
№2. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
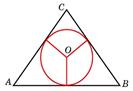
Воспользуемся формулой радиуса окружности вписанной в треугольник:
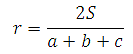
где a, b, c – стороны треугольника
S – площадь треугольника
Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:
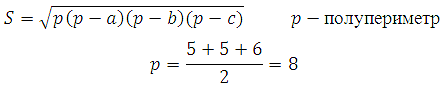
Тогда
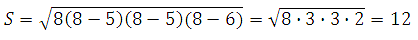
Таким образом:
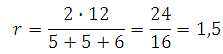
Ответ: 1,5
Домашняя работа. Конспект
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|

 .
.