Тема:Иррациональная функция.. Цель: систематизировать и обобщить изученный материал по данной теме, выработать умения решать задачи.. По графикам известных Вам функций исследовать свойства функции при чётном и нечётном n, выполнить упражнения и ответить

Урок

Тема:Иррациональная функция.

Цель: систематизировать и обобщить изученный материал по данной теме, выработать умения решать задачи.

Задание к уроку:

По графикам известных Вам функций исследовать свойства функции при чётном и нечётном n, выполнить упражнения и ответить на контрольные вопросы.

Краткая теория

Определение. Функция называется иррациональной, если переменная величина находится под знаком корня.

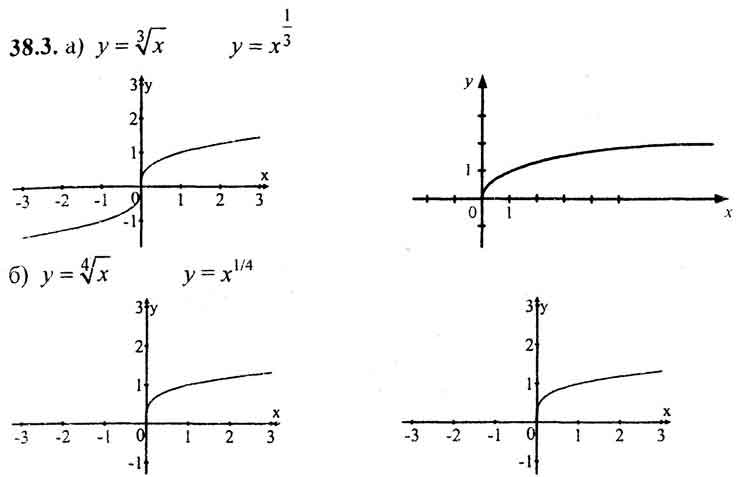На рисунках представлены графики функций:

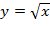
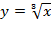
Прочитайте по графикам свойства этих функций.

1. D(y)=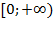

2. E(y)=

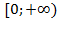3. Монотонно возрастает 4. Непрерывна 5. Ограничена снизу

1. D(y)=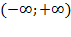

2. E(y)=

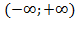3. Монотонно возрастает 4. Непрерывна 5. Не ограничена

При чётном n график функции 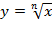обладает теми же свойствами, что и график .

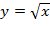При нечётном n график функции 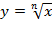обладает теми же свойствами, что и график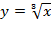

Рассмотрим примеры:

Пример 1: Найти область определения функции f(x) =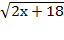

Решение: Чтобы найти область определения данной функции, надо решить неравенство 2x-18³ 0 2x³ -18 x ³ -9

Ответ: D(f) = [ -9; + )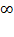

Пример: Найти область определения функции f(x) =

Решение: Чтобы найти область определения данной функции, надо решить неравенство 5x² -4x – 1 ³ 0. Данный квадратный трехчлен имеет корни -1/5 и 1. Так как a = 5 > 0, то ветви параболы направлены вверх. Следовательно наш квадратный трехчлен неотрицателен при x Є (- ∞; -1/5] и [ 1; +∞)

Ответ: D(f) = ( -∞; -1/5] и [ 1; + ∞)

12 Следующая ⇒