Контакты

Случайная статья

Схема полного исследования функции.

Схема полного исследования функции.

1) Область определения функции.

2) Чётность, нечётность.

3) Периодичность.

4) Точки пересечения с осями.

5) Точки разрыва, вертикальные асимптоты.

6) Интервалы монотонности, точки экстремума.

7) Точки перегиба, интервалы выпуклости и вогнутости.

8) Наклонные, горизонтальные асимптоты.

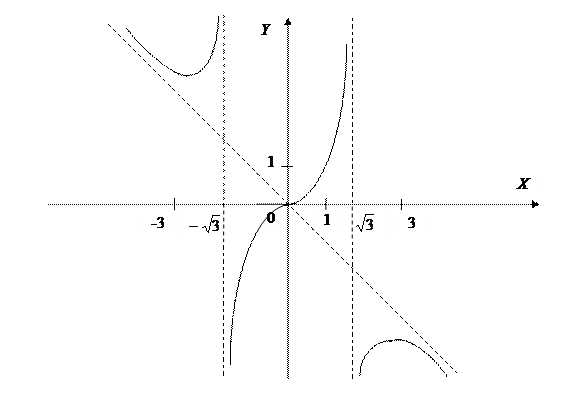
Пример: Исследуйте функцию и постройте её график.

Решение.

1)

2) 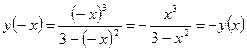- функция нечётная, график симметричен относительно начала координат;

3) функция непериодическая;

4) точка пересечения с осями Ox и Oy - ;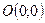

5) найдём односторонние пределы для точек разрыва:

; ;

; .

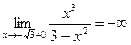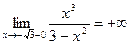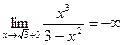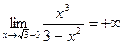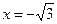- точка разрыва второго рода;

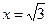- точка разрыва второго рода.

Прямые 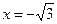, 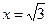- вертикальные асимптоты.

6) найдём первую производную функции :

;

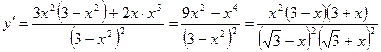из уравнения 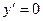получаем критические точки , , .

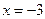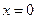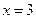Определяем знаки первой производной.

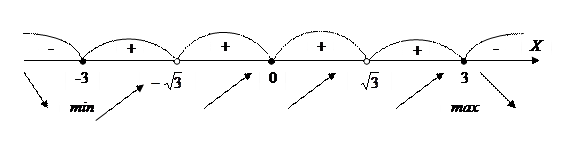
В результате получаем две точки экстремума 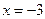и 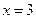. Находим значения функции в этих точках: , .

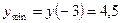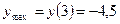7) найдём вторую производную функции :

;

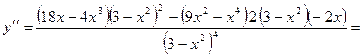
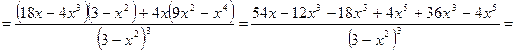
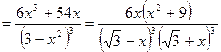при 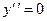получаем точку .

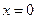Определяем знаки второй производной.

Точка 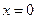является точкой перегиба. На интервалах и 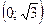график функции вогнутый, а на интервалах 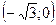и 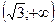– выпуклый.

8) найдём коэффициенты k и b:

; .

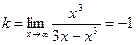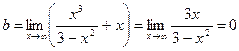Уравнение наклонной асимптоты имеет вид .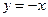

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.