Контакты

Случайная статья

Метод Крамера (используется только в том случае, если число уравнений равно числу неизвестных).

⇐ ПредыдущаяСтр 2 из 2

Метод Крамера (используется только в том случае, если число уравнений равно числу неизвестных).

Пусть дана система 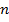линейных уравнений с 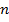неизвестными

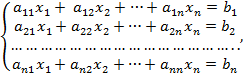
причем 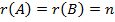, т. е. система имеет единственное решение. Пусть 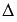- определитель основной матрицы системы, а 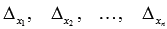- определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

...,

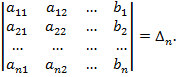
Таким образом, получаем формулы для нахождения значений неизвестных, которые называются формулами Крамера.

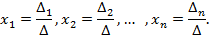
Пример 1.Решить методом Крамера следующую систему линейных уравнений .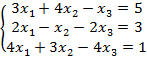

Решение. Найдем определитель основной матрицы системы

.

Так как 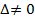, то 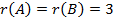, система имеет единственное решение.

Найдем остальные определители для формул Крамера

,

,

.

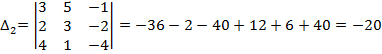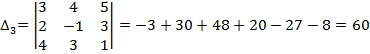По формулам Крамера находим значения переменных

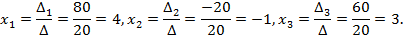
Ответ: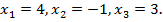

Метод Гаусса.

Метод заключается в последовательном исключении переменных.

Пусть дана система 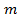линейных уравнений с 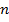неизвестными.

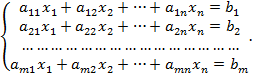
Процесс решения по методу Гаусса состоит из двух этапов:

На первом этапе расширенная матрица системы приводится с помощью элементарных преобразований к ступенчатому виду

,

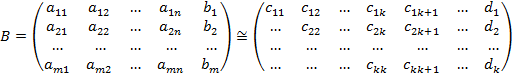Пример 2. Решить методом Гаусса следующую систему

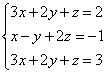
Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду

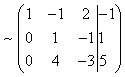
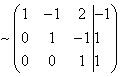
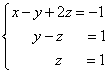
Решение найдём "с конца" - обратный ход. Для этого из последнего уравнения определим z:
.
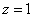Подставив это значение в предшествующее уравнение, найдём y:

Из первого уравнения найдём x:

Ответ: .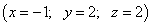

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.