
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ
РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ
Рассмотрим еще примеры нахождения действительных решений систем уравнений.
ìx + y = 12,
| í |
ïî x + y
= 3 .
 Если (х; у) – решение этой системы уравнений, то х ≠ 0 и у ≠ 0. Запишем второе
Если (х; у) – решение этой системы уравнений, то х ≠ 0 и у ≠ 0. Запишем второе
уравнение системы так:
x + y = 3 .
xy 8
Подставляя значение х + у = 12 в полученное уравнение, находим 12 = 3 , откуда ху = 32.
xy 8
Решение данной системы свелось к решению системы
ìx + y = 12,
| î |
Пользуясь теоремой, обратной теореме Виета, получим х1 = 4, у1 = 8, х2 = 8, у2 = 4.
 Ответ: (4; 8), (8; 4).
Ответ: (4; 8), (8; 4).
ìïx - y2 = 3,
| î |
= 28.
 Выразим у2 из первого уравнения системы и подставим это выражение во второе уравнение:
Выразим у2 из первого уравнения системы и подставим это выражение во второе уравнение:
у2 = х – 3, х(х – 3) = 28, х2 – 3х – 28 = 0, откуда х1 = 7, х2 = –7.
Пользуясь формулой у2 = х – 3, находим значение у: если х = 7, то у2 = 7 – 3, у2 = 4, откуда у = 2 или у = –2; если х = –4, то у2 = –4 – 3 = –7 < 0, поэтому действительных корней нет.
 Ответ: (7; 2), (7; –2).
Ответ: (7; 2), (7; –2).
Эту систему уравнений можно было решить иначе.
ìïx + (- y2 )= 3,
| î |
íïx(- y2
)= -28,
можно было составить по теореме, обратной
теореме Виета, уравнение z2 – 3z + 28 = 0; решив это уравнение, получим z1 = x = 7, z2 = x = – 4, откуда, естественно, получим тот же ответ.
Заметим, что замена х через у из первого уравнения и подстановка найденного выражения во второе уравнение привели бы к решению биквадратного уравнения.
ìïx3 - y3 = 7,
ìïx2 - 2xy + 4 y2 = 7,
| î |
+ 8 y3
= 35.
 Применяя формулу суммы кубов, запишем второе уравнение системы в виде
Применяя формулу суммы кубов, запишем второе уравнение системы в виде
(x + 2y)(x2 - 2xy + 4y2 )= 35.
Используя первое уравнение системы, находим х + 2у = 5.
Выразим из этого уравнения 2у через х и подставим найденное выражение во второе уравнение системы: 2у = 5 – х, х2 + (5 – х)2 = 35, откуда
х3 + 125 – 75х + 15х2 – х3 = 35, 15х2 – 75х + 90 = 0.
х2 – 5х + 6 = 0; х1 = 3, х2 = 2.
Теперь находим соответствующие значения у: 2у = 5 – 3, откуда у1 = 1,
2у = 5 – 2, откуда у2 = 3 .
Ответ: (3; 1), (2; 3/2)
| î |
Задача 4*.При каких значениях а система уравнений
решение (х; у), где х = 1?
íax + y = 8
имеет
Если х = 1 входит в решение системы, то получаем следующую систему двух
ì1+ ay2 + y2 = 25,
уравнений относительно у и а: í
îa + y = 8.
Решая эту систему уравнений способом подстановки, получаем
а = 8 – у, 1 + (8 – у)у + у2 = 25,
откуда 1 + 80 – у2 + у2 = 25, 8у = 24, у = 3. Поэтому а = 8 – у, т.е. а = 5. 
Ответ: а = 5.
Домашнее задание
Решить систему уравнений
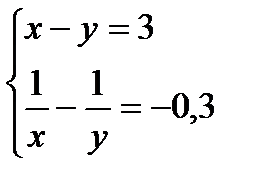
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|