Хелпикс

Главная

Контакты

Случайная статья



Разбор задач к первому коллоквиуму 1 семестра



Разбор задач к первому коллоквиуму 1 семестра

Билет № 21 (дополнительный)

 

Задание повышенной сложности на оценку 5++ (после ответа по билетам).

 

В систему объемом 40 л ввели 4 моль красного фосфора (Р) и 5,5 моль хлора (Cl2). Систему нагрели до 214 °С. В ней установилось равновесие

 

P4 + 6Cl2 = 4PCl3 (все вещества – газы),

 

а равновесное давление газа составило 5 атм.

Найти равновесные количества всех молекулярных форм в системе (P4, Cl2, PCl3) и константу равновесия KP при данной температуре.

 

Решение

Обозначим за x¢, y¢ и z¢ давления паров P4, Cl2 и PCl3 соответственно.

За x, y и z обозначим числа молей P4, Cl2 и PCl3 соответственно.

Тогда по закону Дальтона получаем

x¢ + y¢ + z¢ = P,                                               (1)

где P – общее давление в системе.

Запишем закон сохранения по фосфору. Этот закон показывает, что число атомов фосфора до и после реакции остается неизменным.

Для этого закона получаем 4x + 0y + z = B или

4x + z = B                                                    (2)

где B – число молей фосфора в расчете на атомы. (У нас B = 4 мол.).

Аналогично для закона сохранения по (атомам) хлора. Имеем:

0x + 2y + 3z = C, где С – число молей атомов хлора. Последних вдвое больше, чем исходных молекул хлора (У нас С = 5,5×2 = 11 мол.) Итак

2y + 3z = C                                                    (3)

Если бы уравнение (1) содержало числа молей, а не давления, то мы бы получили систему из трех уравнений с тремя неизвестными. Однако от парциальных давлений к числам молей легко перейти, если уравнение (1) умножит на величину (V/RT). Тогда, согласно закону идеального газа получаем

x + y + z = PV/RT,                                                   (1¢)

где P – общее давление в системе. Обозначая для краткости записи

PV/RT = A, получаем систему из трех уравнений с тремя неизестными x, y и z.

В нашем случае A = 5×101325×40×0,001/(8,314×(273+214)) » 5

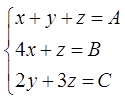                                                                    (4)

Или в нашем случае

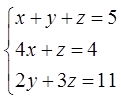                                                                     (5)

Решение системы дает:

x = n(P4) = ½ мол.;

y = n(Cl2) = 2,5 мол.;

z = n(PCl3) = 2 мол.

Соответствующие величины парциальных давлений вычислим, также исходя из уравнения идеального газа:

pi = niRT/V или

p(P4) = ½×8,314×(273+214)/0,04 » 50000 Па » 0,5 атм;

p(Cl2) = 2,5 атм;

p(PCl3) = 2 атм.

 .


 

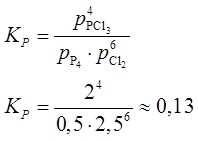Билет №12

2. Известно, что при стандартном давлении и любых температурах a-карбин
(–СºС–)n является метастабильной фазой углерода и самопроизвольно превращает­ся в графит. Известно, что озон разлагается до О2 также со значительным тепловыделением. Доказать, что реакция

3Скарбин + 2O3газ = 3CO2газ

сопровождается большим выделением теплоты (в расчете на одно и то же количество газообразного СО2), чем реакция между графитом и кислородом в тех же условиях. Принять, что энтропии графита и карбина одинаковы.

Решение

Запишем цикл согласно закону Гесса.

                                                             DrH1

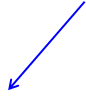
Скарбин + 2/3O3газ                            CO2газ

 

              DrH3 (< 0)                                                 DrH2

                                                   DrH4 (< 0)

 Сграфит (+2/3O3) 2/3O3газ                                       O2газ (+Сграфит)

 

Исходя из полученного цикла получаем:

DrH1 = DrH2 + DrH3 + DrH4.

Т.к. DrH3 и DrH4 < 0, то DrH1 имеет более отрицательное значение, чем DrH2.

Это значит, что в одинаковых условиях тепловыделение Q1 > Q2. Что и требовалось доказать.

Теперь докажем строго, что DrH3 действительно < 0.

DrG3 < 0.

Это по условию задачи (раз процесс самопроизвольный в закрытой системе).

DrG3 = DfGграфит – DfGкарбин = DfHграфит – T×Sграфит – DfHкарбин + T×Sкарбин

Отсюда DrG3 < 0 возможно только при DfHграфит – DfHкарбин < 0.

Но DfHграфит – DfHкарбин = DrH3.

 


 

Билет № 18

 

1. Гомогенные и гетерогенные равновесия.

 

2. Рассчитайте тепловой эффект образования гексагидрата нитрата магния Mg(NO3)2×6H2O, если известны следующие данные:

Mg(мет.) + 2H+(p-p) = Mg2+(p-p) + H2­;                        DH1 = –465,8 кДж/моль;

H2 +N2 + 3O2 = 2H+(p-p) + NO3–(p-p)                         DH2 = –409,4 кДж/моль;

Mg(NO3)2×6H2O = Mg2+(p-p) + NO3–(p-p) + 6H2O(ж.)        DH3 = +21,3 кДж/моль;

H2 + ½O2 = H2O(ж.)                                             DH4 = –285,8 кДж/моль.

Если агрегатное состояние вещества не указано, считать его газом.

Решение

Запишем цикл согласно закону Гесса.

                                              DrH0

Mg + N2 + 3O2 + 6(H2+½O2)                             Mg(NO3)2×6H2O

 

DrH1      + 2H+(p-p)

 

Mg2+(p-p) + H2 {+ N2 + 3O2 + 6(H2+½O2)}

 

DrH2     H2 +N2 + 3O2 = 2H+(p-p) + NO3–(p-p) (+ Mg2+)

 

2H+(p-p) + NO3–(p-p) (+ Mg2+) {+ N2 + 3O2 + 6(H2+½O2)}

 

6×DrH4   6(H2 + ½O2) = 6H2O(ж.) {2H+(p-p) + NO3–(p-p) + Mg2+)}

 

6H2O(ж.) {2H+(p-p) + NO3–(p-p) + Mg2+)}

 

–DrH3                          Mg2+(p-p) + NO3–(p-p) + 6H2O(ж.) {2H+(p-p)}

 

Mg(NO3)2×6H2O {+2H+}

Итого: DrH0 = DrH1 + DrH2 +6DrH4 – DrH3
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.