Контакты

Случайная статья

контрольная работа № 2. по теме: «векторы». Вариант 1. контрольная работа № 2. Вариант 2

контрольная работа № 2

по теме: «векторы»

Вариант 1

1. Векторной величиной является:

а) масса тела

б) скорость тела

в) время

г) площадь.

2. На рисунке АВСD – ромб. Тогда вектор будет равен вектор:

а)

б)

в)

г)

3. Равенство называется:

а) переместительным законом

б) сочетательным законом

в) правилом параллелограмма

г) правилом треугольника

4. Вектор является суммой векторов и на рисунке:

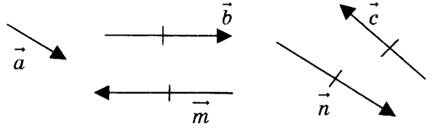5. На рисунке изображены векторы. Вектором, равным вектору , будет вектор:

а)

б)

в)

г)

6. Начертите два неколлинеарных вектора и . Постройте векторы, равные:

а)

б)

7. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.

8. На стороне ВС ромба ABCD лежит точка К так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы и .

контрольная работа № 2

по теме «векторы»

Вариант 2

1. Коллинеарные сонаправленные векторы изображены на рисунке:

2. На рисунке АВСD – прямоугольник. Тогда вектор будет равен вектору:

а)

б)

с)

д)

3. Равенство + = , где А, В, С – произвольные точки, называется:

а) переместительным законом

б) сочетательным законом

в) правилом параллелограмма

г) правилом треугольника

4. Вектор является разностью векторов и на рисунке:

5. На рисунке изображены векторы. Вектор, равный вектору , будет вектор:

а)

б)

в)

г)

6. Начертите два неколлинеарных вектора и . Постройте векторы, равные:

а)

б)

7. В равнобедренной трапеции один из углов равен 60⁰, боковая сторона равна 8 см, а меньшее основание 7 см. найдите среднюю линию трапеции.

8. На стороне СD квадрата ABCD лежит точка Р так, что СР = PD, О – точка пересечения диагоналей. Выразите векторы , , через векторы и .

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.