
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача о диете. Транспортная задача. Задача о раскрое
Задача о диете
|
| в 100гр продукта | Норма потребления | min | max | ||
| масло | мясо | хлеб | сок | |||
| калории | ||||||
| белок | 0,6 | |||||
| жир | ||||||
| углеводы | ||||||
| холестерин | 0,16 | 0,08 | 0,5 | |||
| цена | ||||||
| х1 | х2 | х3 | х4 | |||
2400 ≤ 800x1 + 280x2 + 246x3 + 80x4 ≤ 2800
0,6x1 + 16x2 + 8x3 = 60
0 ≤ 20x1 + 5x2 ≤ 30
10 ≤ 5x3 + 10x4 ≤ 40
0 ≤ 0,16x1 + 0,08x2 ≤ 0,5
x1, x2, x3, x4 ≥ 0
z = 30x1 + 40x2 + 5x3 + 10x4 → min
Транспортная задача
В пунктах А1, …, Аm производится продукт в количествах a1, …, am
В пунктах B1, …, Bn продукт потребляют в количествах b1, …, bn
Дана C = (cij) mxn
cij – стоимость перевозки единицы товара от Ai к Bj
Требуется:
1) От каждого Ai все вывезти;
2) Заявку каждого Bj выполнить;
3) Минимизировать общую стоимость перевозки;
Переменные:
xij – количество товара, перевозимого от Ai к Bj
ai = xi1 + … + xin 1 ≤ i ≤ m
bj = x1j + x2j + … + xmj 1≤ j ≤ n
xij ≥ 0
z = ∑ xijcij → min
Теорема. Транспортная задача имеет решение тогда и только тогда, когда ∑ai = ∑bi.
Задача о раскрое
45см х 90 (х1)
50см х 96 (х2)
65см х 88 (х3)
85см х 56 (х4)
а) → min общими отходами
184 = 4 х 45 х1
184 = 3 х 50 х2
184 = 2 х 65 х3
184 = 2 х 85 х4
4х1 ≤ 90
3х2 ≤ 96
2х3 ≤ 88
2х4 ≤ 56
х1, х2, х3, х4 ≥ 0
z = 4x1 + 3x2 + 2x3 + 2x4 → min
б) потребление min количества листов
x1, x2, x3, x4 ≥ 0
x1, x2, x3, x4 - целые
x1 + x2 + x3 + x4 → min
Сведение к симплексной форме:
x1 + x2 ≤ 1
x1 – 3x2 ≥ -3
Сведение к неотрицательным переменным:
x1= y1 – y2; yi, zj ≥ 0
x2 = z1 – z2
y1 – y2 + z1 – z2 ≤ 1
y1 – y2 – 3z1 + 3z2 ≥ -3
y1, y2, z1, z2 ≥ 0
Процесс выравнивания:
y1 - y2 + z1 – z2 + t1 = 1
y1 – y2 -3z1 + 3z2 – t2 = -3
y1, y2, z1, z2, t1, t2 ≥ 0
Свободные члены ≥0
y1 – y2 + z1 – z2 + t1 = 1 Симплексная форма
-y1 + y2 + 3z1 – 3z2 + t2 = 3
y1, … t2 ≥ 0
Условия, характ. симплексную форму:
а) неизвестные ≥ 0
б) ограничение уравнения
в) свободные члены ≥ 0
Прямая задача линейного программирования
а11 х1 + … + а1n xn ≤ b1
an1 x1 + … + amn xn ≤ bm
x1, …, xn ≥ 0
z= p1 x1 + … + pn xn -> max
Опр. Подмножество М в Rn выпукло, если из А, В ∈ М => [А ; B] ∈ М
Т. С-ма неравенства прямой задачи ЛП задает замкнутое выпуклое мн-во.
Опр. Подмножество М в Rn замкнуто, если предел любой сходящейся последовательности из М содержатся в М.
Т. Если с-ма неравенства прямой задачи ЛП имеет ограниченное мн-во решений. То задача ЛП имеет решение.
Опр. Вершина в прямой задачи.
Выберем из всех неравенство n неравенство. Превратим их в уравнение. Получается с-ма из n уравнений с n неизвестными. Пусть оно имеет ед. решение,, которое удовлетворяет отсальным неравенствам. Тогда это решение наз. Вершиной.
Т. Max z, если он существует, достигается в вершине.
Выпуклым многогранным множеством(ВММ)-назыв. пересечение семейства
полупространств.
Х ∈ Ω назыв. угловой точкой (вершиной) выпуклого многогранного множества Ω, если
она не является внутренней точкой какого-либо отрезка с концами в Ω:
Задание выпуклого многогранника с помощью уравнений и неравенств.
Пусть грани выпуклого многогранника лежат в плоскостях, задаваемых уравнениями
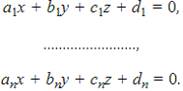
Y
Тогда сам многогранник является пересечением соответствующих полупространств и,следовательно, для его точек должна выполняться система неравенствY которая и определяет этот многогранник.
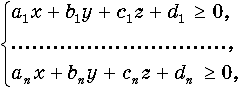
Прямая задача ЛП Двойственная задача
a11 x1 + … + am xn ≤ b1 y1a1 + … + yn am1 ≥ p1
am1 x1 + … + amn xn ≤ bm y1an + … + yn amn ≥ pn
x1, …, xn ≥ 0 y1…yn ≥ 0
z= p1x1 + pnxn -> max t = b1y1 + … + bm ym -> min
a11 …… am1 p1 a11 ….. a1n b1
……………………….. -------> ………………………….
a1n…….amn pn am1…..amn bm
b1………bn 0 p1……..pn 0
Теорема: пусть неравенства в прямой задаче и в двойственной задаче имеют решения. Тогда обе задачи имеют решение и ответы совпадают ( max z = min t)
Пусть х* = ( x*1, …. х*n) – точка макс z
Y* = ( y*1, …, y*m) – точка мин t
Тогда ∀j = 1, …, m ∀i=1, …, n
y*j ( aj1x*1 + … + ajn x*n – bi) = 0 y*I ( y*1a1i + … + y*ma mi)=0
Пусть y*j >0
Aj1x*1 + … + ajnx*n = bj
Дает возможность найти вершину х*, ulе достигается макс z
y*j>0 => j-ый ресурс будет полностью израсходован
Вопрос о дефиците( из производственной задачи):
I(x1) II(x2) Запас
Товары R1 0,5 0,7 100
R2 0,6 0,4 200
R 3 0,3 0,5 150
Отпускная 10 20
цена
0,5x1 + 0,7x2 ≤ 100 Оказалось, что yj*> 0, что,
0,6x1 + 0,4x2 ≤ 200 что jый ресурс будет израсход.
0,3x1 + 0,5x2 ≤ 150 полностью.
z= 10x1+20x2 max
В пунктах А1, …, Аm производится продукт в количествах а1, …,аm. В пунктах B1, …, Bn продукт потребляется в количествах в1, …, вn
Дано С= ( сij) myn ; Cij – стоимость перевозки единицы товара от Аi к Bj
Требуется:
а) от каждого Аi все вывести
б) заявку каждого Bj выполнить
в) минимизировать общую стоимость перевозки
Переменные:
Xij – кол-во товара, перевозимого от Аi к Bj
ai = Xi1 + Хin; j≤ I ≤ m
bj = X1j + X2j + … + Xmj; i≤ j ≤ n
xi j≥ 0 z=
Т: транспортная задача имеет решение тогда и только тогда =
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления (производства) 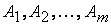 в n пунктов назначения (потребления)
в n пунктов назначения (потребления) 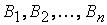 . При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через
. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через 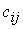 тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через
тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через 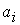 – запасы груза в i-м пункте отправления, через
– запасы груза в i-м пункте отправления, через 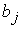 – потребности в грузе в j-м пункте назначения, а через
– потребности в грузе в j-м пункте назначения, а через 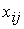 – количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения.
– количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения.
Составим математическую модель задачи. Найти наименьшее значение линейной функции
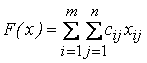 (12.1)
(12.1)
при условиях
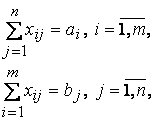
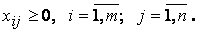 (12.2)
(12.2)
| Пункты отправления | Пункты назначения | Запасы | ||||

| 
| 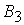
| … | 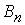
| ||
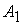
| 
| 
| 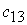
| … | 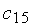
| 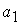
|
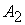
| 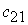
| 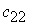
| 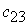
| … | 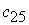
| 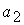
|
| … | … | … | … | … | … | … |
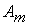
| 
| 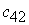
| 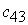
| … | 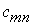
| 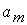
|
| Потребности | 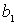
| 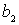
| 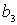
| … | 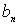
| |
План 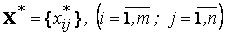 , при котором функция (12.1) принимает свое минимальное значение, называется оптимальным планомтранспортной задачи. Обычно исходные данные транспортной задачи записывают в виде таблицы.
, при котором функция (12.1) принимает свое минимальное значение, называется оптимальным планомтранспортной задачи. Обычно исходные данные транспортной задачи записывают в виде таблицы.
ТеоремаДля разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство
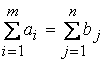 (12.3)
(12.3)
Модель такой транспортной задачи называется закрытой, или замкнутой, или сбалансированной, в противном случае модель называется открытой.
В случае 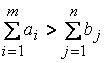 вводится фиктивный (n + 1)-й пункт назначения с потребностью
вводится фиктивный (n + 1)-й пункт назначения с потребностью 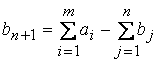 и соответствующие тарифы считаются равными нулю:
и соответствующие тарифы считаются равными нулю:  аналогично, при
аналогично, при 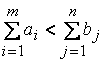 вводится фиктивный (m + 1)-й пункт отправления с запасом груза
вводится фиктивный (m + 1)-й пункт отправления с запасом груза 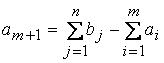 и тарифы полагаются равными нулю:
и тарифы полагаются равными нулю: 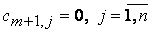 .
.
Этим задача сводится к обычной транспортной задаче. В дальнейшем будем рассматривать закрытую модель транспортной задачи. Число переменных 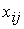 в транспортной задаче с m пунктами отправления и n пунктами назначения равно mn, а число уравнений в системе (12.2) m + n. Так как мы предполагаем выполнение условия (12.3), то число линейно независимых уравнений равно m + n – 1. Следовательно, опорный план может иметь не болееm + n – 1 отличных от нуля неизвестных. Если в опорном плане число отличных от нуля компонент равно в точности m + n – 1, то план называется невырожденным, а если меньше – то вырожденным.
в транспортной задаче с m пунктами отправления и n пунктами назначения равно mn, а число уравнений в системе (12.2) m + n. Так как мы предполагаем выполнение условия (12.3), то число линейно независимых уравнений равно m + n – 1. Следовательно, опорный план может иметь не болееm + n – 1 отличных от нуля неизвестных. Если в опорном плане число отличных от нуля компонент равно в точности m + n – 1, то план называется невырожденным, а если меньше – то вырожденным.
f1(x)≥0 x=(x1,…, xm)
fm(x)≥0 f(x) – выпуклая функция
z max
f=f(x1,…., xm)= f(x) выпукла вниз, если ∀ x,y и ∀ θ ∈ {0;1]
θf(x)+(1- θ)f(y)≥f(θx+(1- θ)y
Если неравенство строгое ∀ 0< θ <1, то f строго выпукла вниз
f выпукла вверх (вогнута), если θf(x)+(1- θ)f(y)≤f(θx+(1- θy)
θf(x)+(1- θ)f(y)
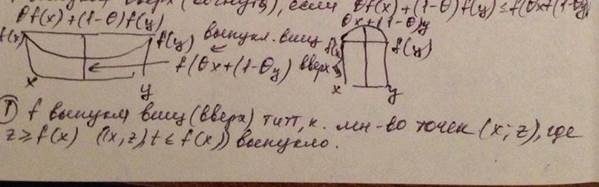
Теорема. (Достаточное условие выпуклости)
Пусть y = f (x) непрерывна на [a,b], и имеет в (a, b) производную до второго порядка включительно, тогда
а) если во всех точках интервала (a, b) вторая производная функции f (x) отрицательна f '' (x) < 0, то кривая на (a, b) выпукла вверх;
b) если во всех точках интервала вторая производная положительна f '' (x) > 0, то кривая на (a, b) выпукла вниз.
Доказательство. Если f''(x)>0, x X, то f'(x) возрастает на множестве X и по предыдущей теореме функция выпукла вниз на множестве X. Аналогично рассматривается случай, когда f''(x)<0
Задача выпуклого программирования - задача оптимизации, целевая функция и допустимое множество которой – выпуклые. Общая задача В. п. состоит в отыскании такого вектора x (т. е. такой точки выпуклого допустимого множества), который доставляет минимум выпуклой функции f(x) или максимум вогнутой функции y(x). Выпуклость (вогнутость) важна тем, что гарантирует нахождение оптимального решения задачи, так как соответственно локальные и глобальный экстремумы здесь обязательно совпадают. Критериями оптимальности в первом случае могут быть, напр., издержки при различных сочетаниях факторов производства, во втором случае — величина прибыли при этих сочетаниях.
Теорема (Необходимое условие экстремума) Если функция нескольких переменных u = f(x1, x2, … , xn) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует.
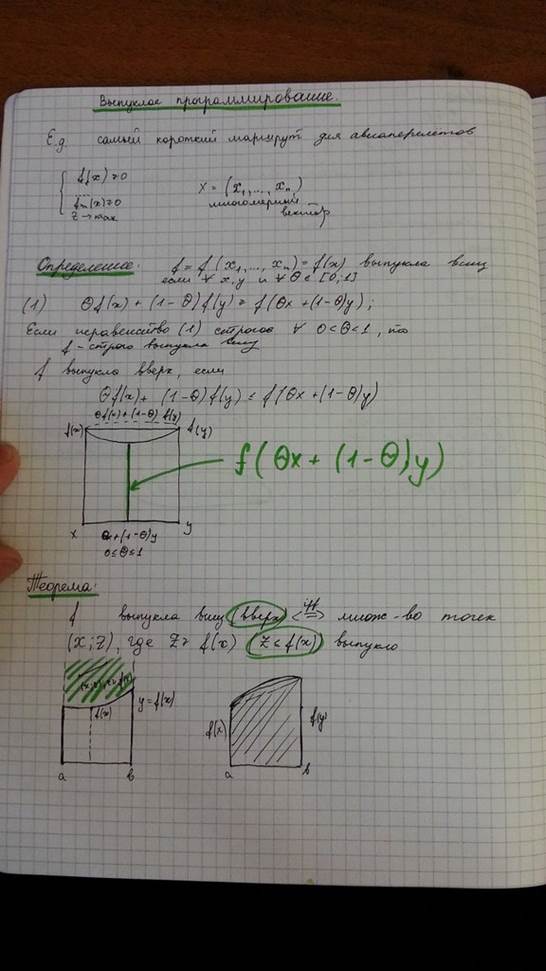






max f(x)
g1(x) ≤C1
…………….
gk(x) ≤ Ck
α=f(x)-j(gj(x)-Cj)
Теорема: если х – точка локального max, то в ней для некоторого набора α1,…, αk ≥0
α’x1=…= α’xn = 0 α’x1 = α’x2 = 0
α j(gj(x)-Cj) = 0 α 1(g1(x)-C1) = 0
α j ≥ 0 => α 1 ≥ 0
gj(x) ≤Cj g1(x) ≤C1
j=1,…k
Достаточное условие максимума. Условие Куна-Таккера
f(x)-> max
g1(x) ≤r1
…………….
gk(x) ≤ r2
x≥0
Условия Куна-Таккера
αx1 ≤ 0, …, α’xn≤ 0 α’α1 ≤ 0, …, α’αn ≥ 0
x1 ≥ 0, …, xn ≥ 0 α 1 ≥ 0, …, α n ≥ 0
x1*α’x1 = 0, …, xn*α’xn = 0 α 1*α’α1 = 0, …, α n*α’αn = 0
Если х удовлетворяет этим условиям, то это будет точка максимума.

. 




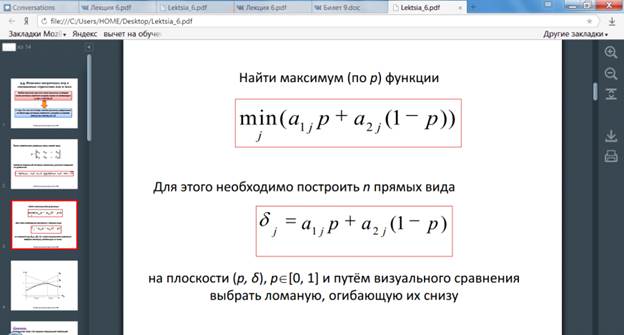
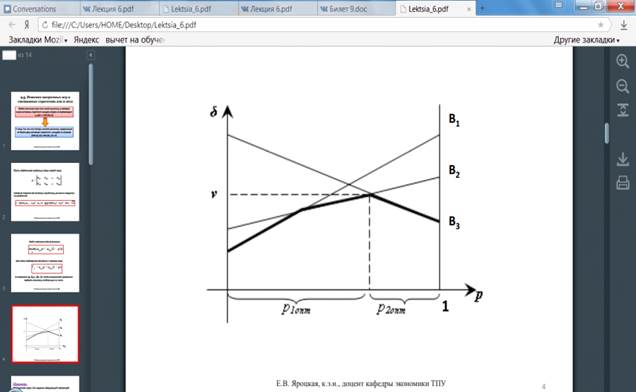
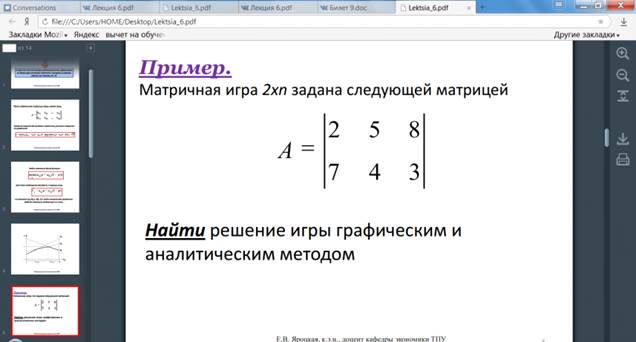
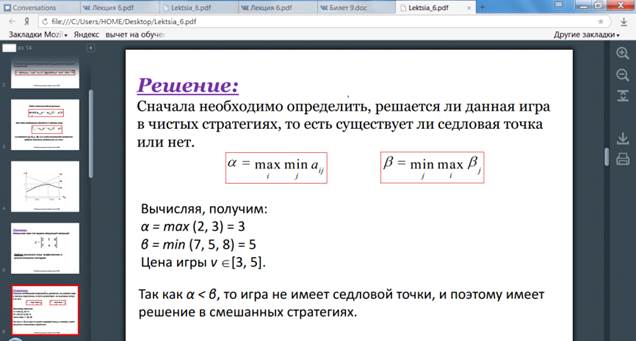
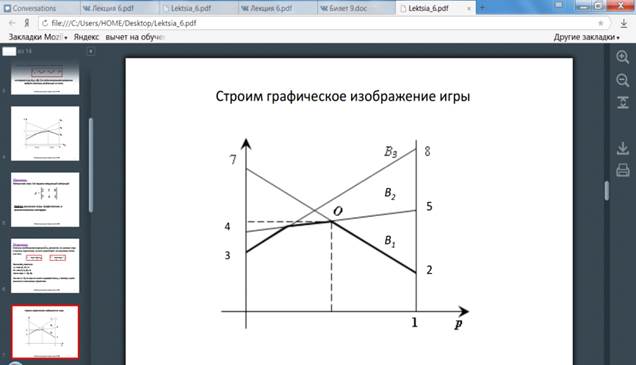
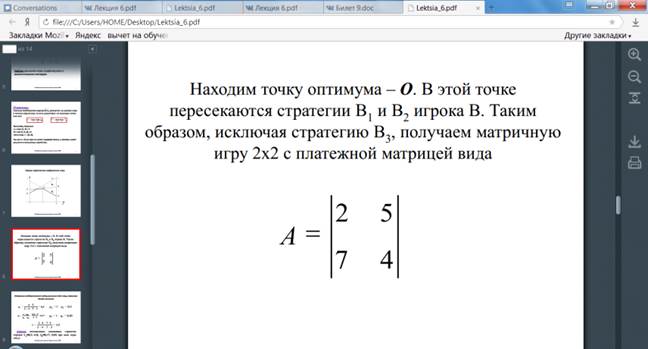
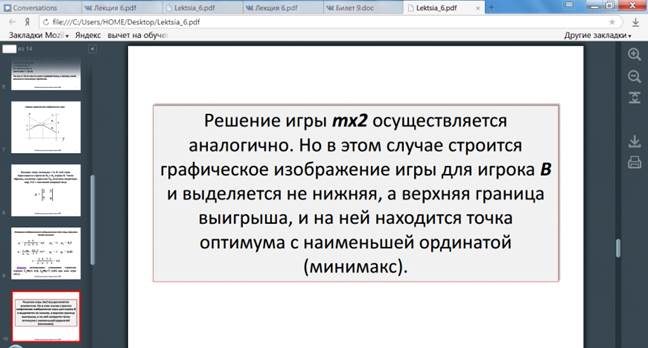
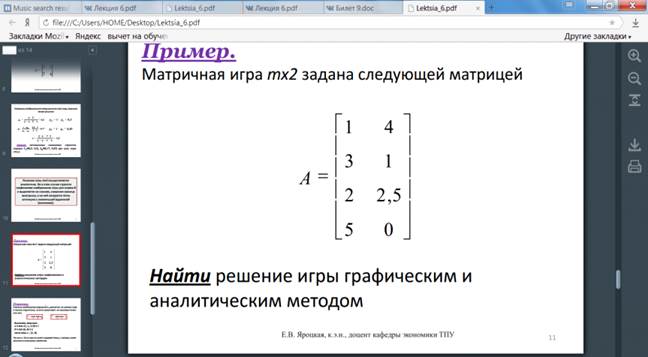
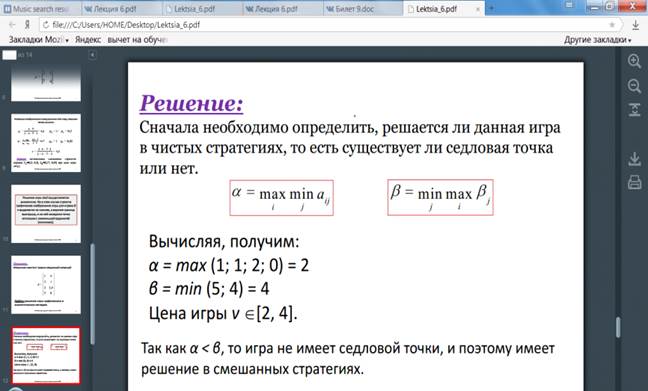
Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.
Критерий Сэвиджа — один из критериев принятия решений в условиях неопределённости. Условиями неопределённости считается ситуация, когда последствия принимаемых решений неизвестны, и можно лишь приблизительно их оценить. Для принятия решения используются различные критерии, задача которых — найти наилучшее решение максимизирующее возможную прибыль и минимизирующее возможный убыток.
Критерий заключается в следующем:
Строится матрица стратегий (платёжная матрица). Столбцы соответствуют возможным исходам. Строки соответствуют выбираемым стратегиям. В ячейки записывается ожидаемый результат при данном исходе и при данной выбранной стратегии.
Строится матрица сожаления (матрица рисков). В ячейках матрицы величина сожаления — разница между максимальным результатом при данном исходе (максимальном числе в данном столбце) и результатом при выбранной стратегии. Сожаление показывает величину, теряемую при принятии неверного решения.
Минимальное решение соответствует стратегии, при которой максимальное сожаление минимально. Для этого для каждой стратегии (в каждой строке) ищут максимальную величину сожаления. И выбирают то решение (строку), максимальное сожаление которого минимально.

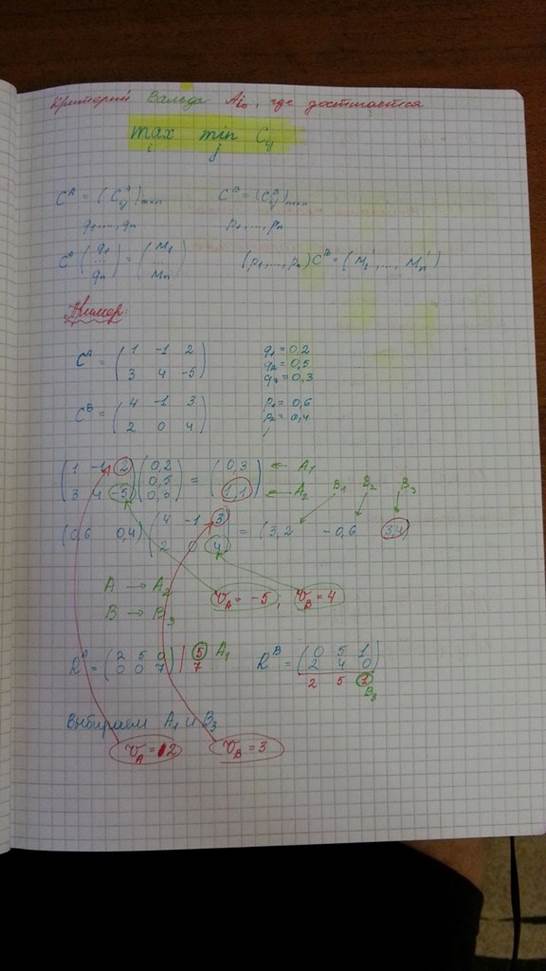







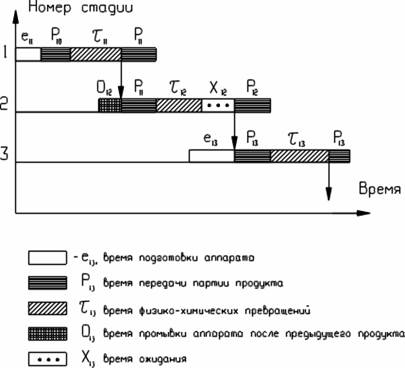
Календарный график строится на основе так называемой диаграммы Ганта. Диаграмма Ганта - это линейный график, задающий сроки начала и окончания взаимосвязанных работ, с указанием ресурсов, используемых для их выполнения.
По сути, диаграмма Ганта состоит из полос, ориентированных вдоль оси времени. Каждая полоса на диаграмме представляет отдельную задачу в составе проекта (вид работы), её концы — моменты начала и завершения работы, её протяженность — длительность работы. Вертикальной осью диаграммы служит перечень задач. Кроме того, на диаграмме могут быть отмечены совокупные задачи, проценты завершения, указатели последовательности и зависимости работ, метки ключевых моментов (вехи), метка текущего момента времени «Сегодня» и др.
СИМПАТИЧНОЕ УТОЧНЕНИЕ: (не обязательно писать это)
В отличие от Gantt Chart (График Гантта), Метод оценки и пересмотра планов (PERT) не предполагает наличия графика, поэтому вы не можете точно следить за тем, когда должна быть выполнена та или иная задача. С другой стороны, в методе PERT проще отслеживать зависимости. Поэтому PERT, как правило, предпочтительнее для более крупных проектов.
Ранний срок начала работы: продолжительность самого длительного пути от начального
события до предшествующего события данной работы.
Ранний срок окончания работы: сумма раннего начала и продолжительности данной работы (если работа начата в ранний срок).
Поздний срок начала работы: это такое допустимое начало работы, которое не вызывает задержки окончания всего комплекса работ.
Поздний срок начала работы определяется путем вычитания из продолжительности критического пути самого длительного пути от предшествующего события данной работы до конечного события.
Поздний срок окончания работы: Сумма позднего начала и продолжительности данной работы, если работа начата в поздний срок
Позднее окончание и начало для всех работ графика определяется последовательно, начиная отсчет не от начального, а от конечного события.
Раннее время меньше позднего, но на критическом пути они равны.
(можно привести пример сетевого планирования, чтобы все стало яснее)
Правило Борда
· Каждый избиратель сообщает свой линейный порядок
предпочтений в виде A>B>C>D
· Каждый за 1 место кандидат получает x1=(n-1) очков; за второе –
x2=(n-2) очков; … за последнее – xn=0 очков.
· В общем случае должны выполняться неравенства:
x1≥x2 ≥ … ≥ xn
· Все очки складываются, итоговый порядок предпочтений
утверждается по убыванию количества очков (при равенстве очков –
кандидаты считаются неразличимыми)
· Правило относительного большинства является частным случаем
правила Борда (x1=1; x2 = … = xn=0)
· Итоговый порядок предпочтений зависит от чисел x1≥x2 ≥ … ≥ xn
· В некоторых случаях правило Борда получает победителя, не
соответствующего победителю по принципу абсолютного
большинства.
Попарные сравнения
(победитель по Кондорсе)
· Есть правило сравнения двух кандидатов между собой
– большинство.
· Победитель по Кондорсе – выигрывает при всех
попарных сравнениях.
Теорема Эрроу: Если число кандидатов не меньше
трех, не существует голосования, удовлетворяющего
трем условиям:
· Условие единогласия
· Условие независимости от посторонних альтернатив
· Условие отсутствия диктатора
Правило большинства
· Голос = фамилия одного кандидата
· Правило большинства – если кто-то набрал больше половины голосов -> победитель
· Иначе результата голосования нет.
· Правило относительно большинства – вне зависимости от
половины кто больше – тот победитель.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|