Прикладная задача.

Прикладная задача.

В 1980 г. в стране было 108,5 тыс. тракторов и получено с одного гектара 8,5 ц зерновых. В 2012 г. в стране было 400 тыс. тракторов и получено с одного гектара 25,9 ц зерновых. Изучить влияние расширения тракторного парка на возрастание урожая зерновых.

	1980 г.	2012 г.
количество тракторов, тыс. штук	108,5
урожайность, ц/ га	8,5	25,9

Решение:

Обозначим время – х, количество тысяч тракторов – у; урожай, полученный с одного гектара, обозначим z (центнеров).

По условию задачи имеем четыре точки:

А (х₁; у₁); х₁ = 1980, у₁ = 108,5;

В (х₂; у₂); х₂ = 2012, у₂ = 400;

С (х₁; z₁); х₁ = 1980, z₁ = 8,5;

D (х₂; z₂); х₂ = 2012, z₂ = 25,9.

Найдем уравнения прямых – графиков возрастания тракторного парка и урожайности зерновых с одного гектара за 1980 – 2012 года в виде y = kx + b, - уравнения прямой с угловым коэффициентом.

Используя уравнение прямой, проходящей через две заданные точки, получаем:

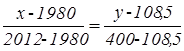
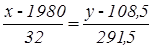
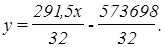
Таким образом, угловой коэффициент прямой возрастания тракторного парка равен:

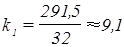
Используя точки С и D, аналогично находим уравнение прямой возрастания урожайности зерновых с одного гектара.

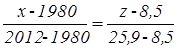
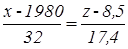
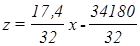
Следовательно, ее угловой коэффициент равняется: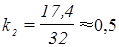

Из условия задачи можно сделать вывод, что с возрастанием тракторного парка урожайность зерновых с 1 га также возрастает. Но угловой коэффициент k₁ графика возрастания количества тракторов значительно больше углового коэффициента k₂ графика возрастания урожайности зерновых, но не пропорционально (9,1 и 0,5 соответственно). Возрастание количества тракторов, т.е. возрастание оснащенности сельского хозяйства, не является основным фактором в повышении его эффективности. Необходимо учитывать влияние других факторов: качества семян, культуру агротехники и т.д.

Вопросы для обсуждения:

1) в какой системе координат можно построить каждую прямую?

2) можно ли построить обе прямые в одной системе, чтобы наглядно увидеть взаимное расположение прямых?

3) какие еще математические модели окружающей действительности вам известны?

4) опишите математическую модель движения автомобиля.