
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача о работе переменной силы на криволинейном участке пути
Задача о работе переменной силы на криволинейном участке пути
Пусть на плоскости задана кривая линия.
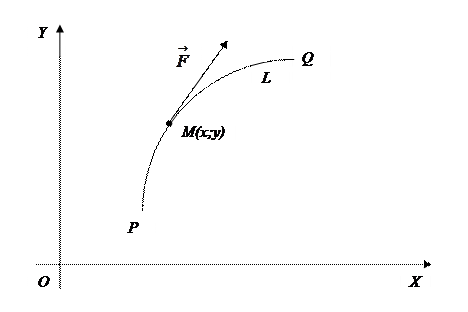
Предположим, что материальная точка M(x;y) перемещается по дуге PQ от точки P до точки Q под действием переменной силы 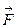 . Сила
. Сила 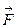 изменяет, вообще говоря, и свою величину, и своё направление в зависимости от перемещения точки M, т.е., в конечном итоге, в зависимости от координат (x;y). Требуется вычислить работу A переменной силы
изменяет, вообще говоря, и свою величину, и своё направление в зависимости от перемещения точки M, т.е., в конечном итоге, в зависимости от координат (x;y). Требуется вычислить работу A переменной силы 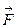 на криволинейном участке пути. Координаты вектора
на криволинейном участке пути. Координаты вектора 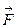 обозначаются обычно через
обозначаются обычно через 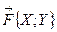 . Очевидно, координаты вектора
. Очевидно, координаты вектора 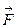 будут зависеть от положения точки M, т.е. от координат (x;y):
будут зависеть от положения точки M, т.е. от координат (x;y):  . Будем предполагать, что эти функции непрерывны в некоторой области D, содержащей линию L. Очевидно:
. Будем предполагать, что эти функции непрерывны в некоторой области D, содержащей линию L. Очевидно:
 . (1)
. (1)
Из формулы (1) следует, что вектор 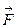 есть переменный вектор, величина и направление которого зависят от двух переменных x и y.
есть переменный вектор, величина и направление которого зависят от двух переменных x и y.
Для решения задачи разделим дугу PQ на n произвольных частей. Рассмотрим i–ую часть дуги PQ: 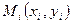 ,
,  ,
, 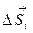 - вектор перемещения на i–ом участке пути. Очевидно, вектор
- вектор перемещения на i–ом участке пути. Очевидно, вектор 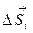 имеет две координаты
имеет две координаты  ,
, 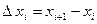 ,
, 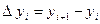 :
:
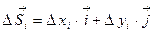 . (2)
. (2)
Далее будем считать, что на i–ом участке пути сила 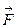 является величиной постоянной, равной значению в точке
является величиной постоянной, равной значению в точке 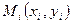 (в силу малости i–го участка пути). Тогда из формулы (1) следует, что
(в силу малости i–го участка пути). Тогда из формулы (1) следует, что
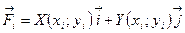 . (3)
. (3)
Далее найдём работу на i–ом участке пути:
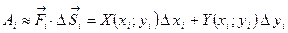 .
.
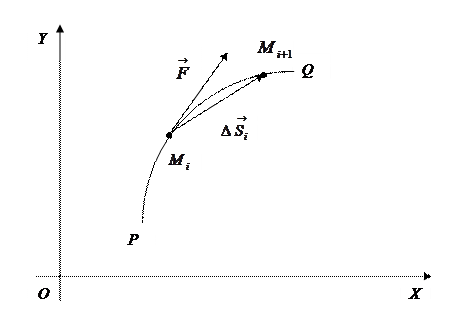
Просуммируем все 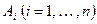 . Получим:
. Получим:
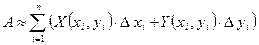 .
.
Перейдём к пределу при 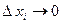 ,
,  , т.е. при
, т.е. при 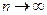 . Получим:
. Получим:
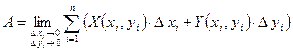 .
.
Полученный предел называют криволинейным интегралом от 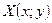 и
и  по дуге PQ, т.е. по кривой L и обозначают:
по дуге PQ, т.е. по кривой L и обозначают:
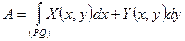 . (4)
. (4)
В частном случае, если PQ - замкнутый контур, т.е. точки P и Q совпадают, то криволинейный интеграл (4) обозначается символом:
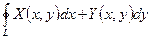 .
.
Этот криволинейный интеграл называется циркуляцией вектора 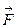 по замкнутому контуру L.
по замкнутому контуру L.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|