Задание 1.. Задание 3.. Задание 4.. Задание 5.. Задание 6.. Задание 7.. Задание 8.. Задание 9.. Задание 10.. Задание 11.. Задание 12.. Задание 13.. Задание 14.. Задание 15.. Задание 16.. Задание 17.. Задание 18.. Условие для заданий 19-21.

Чтобы открыть дополнительные материалы к варианту, скачайте архив на компьютер и переименуйте его, заменив расширение “zip1” на “zip”.

Задание 1.

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах.

	П1	П2	П3	П4	П5	П6	П7
П1
П2
П3
П4
П5
П6
П7

Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта Г в пункт Ж, если передвигаться можно только по указанным дорогам. В ответе запишите целое число — длину пути в километрах.

Задание 2.

Логическая функция F задаётся выражением (x∨ z)∧(y∨z). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

?	?	?	F

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.

Задание 3.

В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Таблица «Магазин» содержит информацию о местонахождении магазинов. На рисунке приведена схема указанной базы данных.

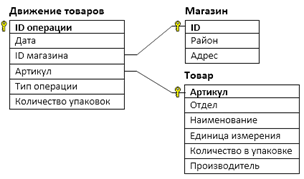
Используя информацию из приведённой базы данных, определите, какова суммарная выручка за товар «сливки 35% для взбивания» в магазинах Заречного района в период с 1 по 5 июня включительно. В ответе запишите только число.

Задание 4.

Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=0, Б=100, В=110. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?

1) 101 2) 10 3) 11 4) 01

Задание 5.

Автомат обрабатывает натуральное число N по следующему алгоритму:
1. Строится двоичная запись числа N.
2. В конец двоичной записи добавляются две первые цифры этой записи в обратном порядке.
3. Результат переводится в десятичную систему и выводится на экран.

Пример. Дано число N = 11 Алгоритм работает следующим образом:
1. Двоичная запись числа N: 1011
2. В конец записи добавляются цифры 01 – первые две цифры в обратном
порядке (сначала вторая, затем первая), получается 101101
3. На экран выводится число 45

При каком наименьшем исходном N результат на экране автомата будет больше 90?

Задание 6.

Сколько различных значений числа d можно ввести, чтобы после выполнения программы было напечатано 171?

Python	Паскаль	Си++
d = int(input()) n = 27 s = 12 while s <= 2019: s += d n += 16 print(n)	var n, s, d: integer; begin readln(d); n := 27; s := 12; while s <= 2019 do begin s := s + d; n := n + 16 end; write(n) end.	#include <iostream> using namespace std; int main() { int n, s, d; cin >> d; n = 27, s = 12; while (s <= 2019) { s += d; n += 16; } cout << n << endl; return 0; }

Задание 7.

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла –8 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в раза 2 выше и частотой дискретизации в 1,25 раз большей, чем в первый раз. Сжатие данных не производилось.
Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Задание 8.

Вася составляет 5-буквенные слова, в которых есть только буквы А, Р, Б, У, З, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

Задание 9.

Откройте файл электронной таблицы, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите количество дней в мае, когда температура в 09:00 была выше, чем средняя температура в этот день.

Задание 10.

С помощью текстового редактора определите, сколько раз, не считая сносок, встречается местоимение «кто» (со строчной буквы) в тексте романа А.С. Пушкина «Капитанская дочка». В ответе укажите только число.

Задание 11.

При регистрации на сервере каждый пользователь получает уникальный персональный код, состоящий из 21 символа, каждый из которых может быть одной из 26 заглавных латинских букв. При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством бит, а для кода в целом выделяется минимально возможное целое количество байт.
Для хранения данных о 40 пользователях потребовалось 2400 байт. Сколько байт выделено для хранения
дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байт.

Задание 12.

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

заменить (v, w)

нашлось (v)

Если при выполнении команды заменить цепочка, которую нужно заменить, не найдена, то строка не изменяется. Дана программа для исполнителя Редактор:

НАЧАЛО

ПОКА нашлось (56) ИЛИ нашлось (3333)

заменить (56, 3)

заменить (3333, 3)

КОНЕЦ ПОКА

КОНЕЦ

Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 121 строки 563 (563563563…563)?

Задание 13.

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт О, проходящих через пункт Ж?

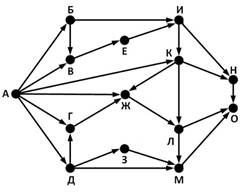
Задание 14.

Значение арифметического выражения: 9⁷+3²¹–19 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?

Задание 15.

Для какого наименьшего целого неотрицательного числа A выражение (3x+5y<A)∨(x≥у)∨(y>8) тождественно истинно при любых целых неотрицательных x и y?

Задание 16.

Алгоритм вычисления функции F(n)F(n), где nn – натуральное число, задан следующими соотношениями:

(n)=n–1 при n<4,

F(n)=n+2∗F(n–1), когда n≥4 и кратно 3,

F(n)=F(n–2)+F(n–3), когда n≥4 и не кратно 3.

Чему равна сумма цифр значения F(25)?

Задание 17.

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 1 до 10 000 включительно. Найдите количество чисел, которые делятся на 5 и не делятся на 6, 10, 15, 16 и максимальное из них. В ответе запишите два целых числа без пробелов и других дополнительных символов: сначала количество, затем максимальное число.

Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц.

Задание 18.

Квадрат разлинован на N×N клеток (1<N<201<N<20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из трёх команд: вправо, вверх или вправо-вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх – в соседнюю верхнюю, а по команде вправо-вверх – на одну клетку вправо и вверх по диагонали. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата записана величина вознаграждения от 1 до 100. Попав в клетку после хода вправо или вверх, Робот получает указанное в ней вознаграждение, а если он попал в клетку после выполнения команды вправо-вверх, вознаграждение удваивается. Это также относится к начальной и конечной клетке маршрута Робота. Определите максимальное и минимальное вознаграждение, которое может получить Робот, пройдя из левой нижней клетки в правую верхнюю. В ответе укажите два числа – сначала максимальное вознаграждение, затем минимальное. Исходные данные записаны в файле в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата.

Условие для заданий 19-21.

За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 71. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 71 или больше камней. В начальный момент в первой куче было 10 камней, во второй куче – S камней; 1 ≤ S ≤ 60

Задание 19.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

Задание 20.

Найдите три таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

− Петя не может выиграть за один ход;

− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания через пробел.

Задание 21

Сколько существует значений S, при которых одновременно выполняются два условия:

– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Задание 22.

Получив на вход число х, этот алгоритм печатает два числа a и b. Укажите наибольшее из таких чисел х, при вводе которых алгоритм печатает сначала 2, а потом 15.

Паскаль	Python	C++
var x, a, b: longint; begin readln(x); a := 0; b := 0; while x > 0 do begin a := a+1; b := b+(x mod 100); x := x div 100; end; writeln(a); write(b); end.	x = int(input()) a = 0; b = 0 while x > 0: a = a + 1 b = b + (x % 100) x = x // 100 print("%d\n%d" % (a, b))	#include <iostream> using namespace std; int main() { int a, b, x; cin << x; a = 0; b = 0; while (x > 0) { a = a+1; b = b+(x % 100); x = x / 100; } cout << a << endl << b; return 0; }

Задание 23.

Исполнитель "Двоечник" преобразует число на экране. У исполнителя есть три команды, которым

присвоены номера:

1 Возводит в квадрат

2 Прибавить 2

3 Умножить на 2

Сколько существует программ, для которых при исходном числе 2 результатом является число 64 и при этом траектория вычислений не содержит число 8?

Задание 24.

В текстовом файле находится цепочка из символов латинского алфавита A, B, C, D, E. Найдите количество цепочек длины 3, удовлетворяющих следующим условиям:

· 1-й символ – один из символов B, C или D;

· 2-й символ – один из символов B, D, E, который не совпадает с первым;

· 3-й символ – один из символов B, C, E, который не совпадает со вторым.

Задание 25.

Назовём нетривиальным делителем натурального числа его делитель, не равный единице и самому числу. Найдите все натуральные числа, принадлежащие отрезку [152346; 957812] и имеющие ровно три нетривиальных делителя. Для каждого найденного числа запишите в ответе само число и его наибольший нетривиальный делитель. Найденные числа расположите в порядке возрастания. Ответ запишите в одну строку, через пробел.

Задание 26.

Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов.

Известно, какой объём занимает файл каждого пользователя. Системный администратор старается сохранить файлы как можно большего размера. При этом используя выделенную память максимально эффективно – сохраняя файлы меньшего размера, если файлы большего не могут быть сохранены.

Входные данные.

В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.

Запишите в ответе два числа: сначала число сохраненных файлов, затем размер наименьшего сохраненного файла. Через пробел.

Пример входного файла:

100 4

При таких исходных данных можно сохранить три файла – 70, 25, 3. Поэтому ответ должен содержать два числа – 3 и 3.

Задание 27.

Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 7 и при этом была максимально возможной. Программа должна напечатать одно число – максимальную возможную сумму, соответствующую условиям задачи.

Входные данные:Даны два входных файла: файл A и файл B, каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 1 000.

Пример входного файла:

1 3

5 12

6 9

7 4

3 3

1 1

Для указанных входных данных значением искомой суммы должно быть число 33.

В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.