Хелпикс

Главная

Контакты

Случайная статья



Практическая работа ___. Расчет сложных цепей постоянного тока методом контурных токов». Цель: научиться решать задачи методом контурных токов. Сделать вывод к работе



Практическая работа ___

«Расчет сложных цепей постоянного тока методом контурных токов»

Цель: научиться решать задачи методом контурных токов

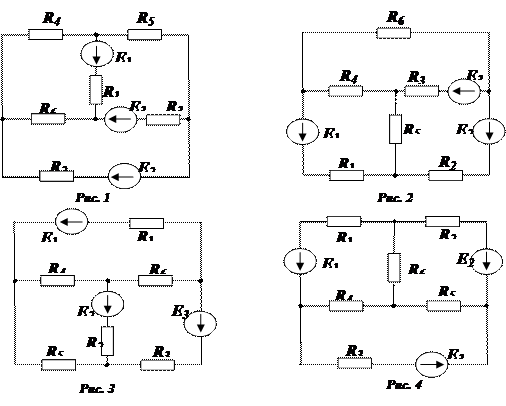
1. Определить токи в ветвях схемы методом контурных токов.

2. Составить уравнение баланса мощностей.

 

№ варианта рис. Е1, В Е2, В Е3, В R1, В R2, В R3, В R4, В R5, В R6, В
1. рис.1.
2. рис.2.
3. рис.3.
4. рис.4.
5. рис.1.
6. рис.2.
7. рис.3.
8. рис.4.
9. рис.1.
10. рис.2.
11. рис.3.
12. рис.4.
13. рис.1.
14. рис.2.
15. рис.3.

 

 

 

Сделать вывод к работе

Методика решения:

 

 

 

 

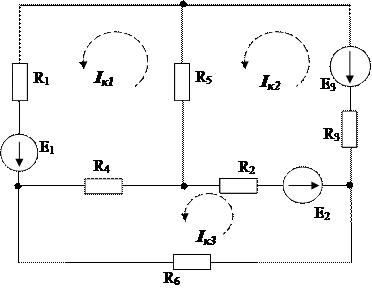
                                           Рис.1

Дано:

 

Е1=100 В;          R2=5 Ом;

Е2=120 В;          R3=16 Ом;

Е3=200 В;          R4=21 Ом;

R1=4 Ом;            R5=15 Ом;

                           R6=23 Ом;

1. Определить токи в ветвях схемы методом контурных токов,

2. Составить уравнение баланса мощностей.

 

Решение: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС, так и величина падения напряжения на элементах может быть, как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

- ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

- напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

1. Составим уравнение для каждого контура по 2 закону Кирхгофа.

 

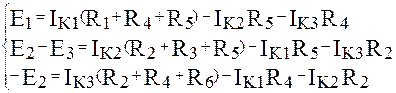
2. Подставим исходные данные в полученную систему уравнений и решим ее относительно неизвестных Iк1, Iк2, I к3:

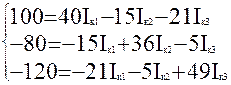
Главный определитель:

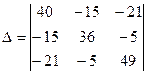= 40·36·49 + (-15) · (-5) · (-21) + (-15) · (-5) · (-21) - (-21) · 36· (-21) -

- (-15) · (-15) · 49 - (-5) · (-5) ·40 = 70560-1575-1575-15876-11025-1000 = 39509

 

Определитель по первому неизвестному:

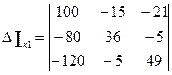= 100·36·49 + (-15) · (-5) · (-120) + (-80) · (-5) · (-21) - (-21) · 36· (-120)- (-15) · (-80) ·49 - (-5) · (-5) ·100 = 176400 – 9000 – 8400 – 90720 – 58800 – 1225 = 8255

 

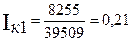 А

Определитель по второму неизвестному:

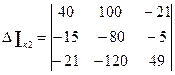= 40· (-80) · 49 + 100· (-5) · (-21) + (-15) · (-120) · (-21) - (-21) · (-80) · (-21) - 100· (-15) · 49 - (-5) · (-120) · 40 = -156800+10500-37800+35280+73500-24000 = -99320

 

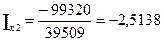 А=-2,51 А

Определитель по третьему неизвестному:

= 40·36·(-120) + (-15) · (-80)·(-21) + (-15)·(-5)·100 - 100·36·(-21) -

- (-15)·(-15)·(-120) - (-80)·(-5)·40 = -172800 – 25200 + 7500 + 75600 + 27000 - 16000=-103900

 

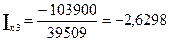 А=-2,63А

 

3.Определим реальные токи в ветвях:

I1 = Iк1 = 0,21 A

I2 = Iк2 - Iк3 = -2,52 - (-2,63) = 0,11 A

I3 = Iк2 = -2,52 A (Ток I3 направлен встречно Iк2)

I4 = Iк1-Iк3 = 0,18 - (-2,63) = 2,81 A

I5 = Iк1- Iк2 = 0,18 - (-2,51)=2,69 A

I6 = Iк3 = -2,63 A (Ток I6 направлен встречно Iк3)

4. Составим уравнение баланса мощностей:

ΣРИСТ=ΣРПОТР

 

ΣРИСТ = Е1I1+Е2I2+Е3I3 =100·0,21+120·0,11+200·2,52=21+13,2+504=538,2 Вт;

 

ΣРПОТР = I12R 1+ I22R2+ I32R3+ I42R4+ I52R5+ I62R6 = 0,212·4 + 0,112·5 + 2,522·16 +

+2,812·21+ 2,692·15++2,632·23 = 0,18 + 0,061+101,61 +165,82 +108,54+159,09=538,3 Вт

 

538,2 Вт ≈ 538,3 Вт

 

Таким образом, баланс мощностей выполняется.

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.