
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие 4. Задание 1
Практическое занятие 4
Тема.Использование математического моделирования в медицине.
Цель –изучить принципы построения и использования математических моделей в медицинских исследованиях.
Задание 1
Определить остаточный объем левого желудочка, конечнодиастолический объем и оценить диастолическую функцию левого желудочка для данных, представленных в таблице 4.1.
Таблица 4.1 – Значения гемодинамических показателей пациентов
| Пол | АДд | t | k | Vуд | АДп |
| Мужской | 79,8 | 0,278 | 68,9 | ||
| Мужской | 72,9 | 0,27 | 72,4 | 43,5 | |
| Женский | 70,3 | 0,306 | 93,3 | 44,2 |
Построение математической модели
Остаточный объем левого желудочка определяет эффективность насосной функции сердца и резервные функциональные возможности миокарда. Определение остаточного объема левого желудочка помогает врачу оценить функцию диастолы миокарда, часто изменяющуюся при ряде заболеваний сердца.
Для нахождения остаточного объема левого желудочка возможно использование математической модели, теоретической основой которой являются известные данные о том, что остаточный объем левого желудочка находится в прямой зависимости от времени изгнания крови сердцем и диастолического давления, а также в обратной зависимости от ударного объема и пульсового артериального давления. Кроме этого, известно, что в норме у здоровых людей Vост составляет приблизительно 40% от конечнодиастолического объема левого желудочка (или 2/3 ударного объема).
Таким образом, математическая модель для расчета объема левого желудочка имеет вид
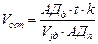 , ,
| (4.1) |
где 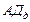 ,
, 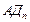 – диастолическое и пульсовое артериальное давление соответственно;
– диастолическое и пульсовое артериальное давление соответственно;
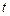 – время изгнания крови;
– время изгнания крови;
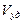 – ударный объем сердца;
– ударный объем сердца;
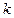 – коэффициент, равный для мужчин 9284; для женщин – 5732.
– коэффициент, равный для мужчин 9284; для женщин – 5732.
Конечнодиастолический объем левого желудочка можно определить, суммируя значения ударного и остаточного объемов
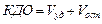 , ,
| (4.2) |
где 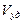 ,
, 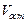 – ударный и остаточный объемы соответственно.
– ударный и остаточный объемы соответственно.
Оценить диастолическую функцию левого желудочка можно, используя формулу
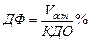 , ,
| (4.3) |
где 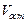 – остаточный объем;
– остаточный объем;
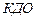 – конечнодиастолический объем.
– конечнодиастолический объем.
За норму берется значение ДФ= 40%.
Ход выполнения
1 Запустить программу Excel. Создать новую книгу C:\User\ЛД???\моделирование.xls, открыть новый лист рабочей книги. Переименовать Лист1 на Задание1.
2 Ввести данные из таблицы 4.1 в электронную таблицу. Оформить их в виде таблицы 4.2.
3 Рассчитать остаточный объем левого желудочка по формуле (4.1). Для этого в ячейку G2 ввести формулу = B2*C2*D2/(E2*F2). Нажать Enter. При помощи автозаполнения заполнить ячейки G3 и G4.
Таблица 4.2
| А | В | С | D | E | F | G | H | I | |
| Пол | АДд | t | k | Vуд | АДп | Vост | КДО | ДФ | |
| Мужской | 79,8 | 0,278 | 68,9 | ||||||
| Мужской | 72,9 | 0,27 | 72,4 | 43,5 | |||||
| Женский | 70,3 | 0,306 | 93,3 | 44,2 |
4 Рассчитать конечнодиастолический объем сердца по формуле (4.2). Для этого в ячейку Н2 ввести формулу = E2 + G2. Нажать Enter. При помощи автозаполнения заполнить ячейки H3 и H4.
5 Оценить диастолическую функцию левого желудочка по формуле (4.3). Для этого в ячейку I2 ввести = G2/H2 Нажать Enter. При помощи автозаполнения заполнить ячейки I3 и I4.
6 Выделить диапазон I2:I4. Выбрать пункт меню Формат, подменю Ячейки. Перейти на закладку Число. Выбрать из списка Числовой формат – Процентный. Нажать Ок.
7 Выделить диапазон G2:H4. Выбрать пункт меню Формат, подменю Ячейки. Перейти на закладку Число. Выбрать из списка Числовой формат – Числовой. Выбрать Число десятичных знаков - 2. Нажать Ок.
8 Записать в тетрадь математическую модель, входные данные и результаты расчетов. Сделать анализ полученных значений ДФ.
Результаты выполнения представлены в приложении В.
Задание 2
Исследовать показатели системной гемодинамики у здоровых людей, пациентов с граничной артериальной гипертензией и больных гипертонической болезнью I стадии для данных, приведенных в таблице 4.3.
Таблица 4.3
| Группа | Vн | Свb | ОПС | Ca | АДср |
Здоровые
ПАГ
ГБ
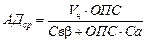 ,
,
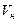 – напряженный объем крови;
– напряженный объем крови;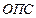 – общее периферическое сопротивление;
– общее периферическое сопротивление;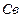 ,
, 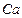 – эластичность венозных и артериальных сосудов соответственно ;
– эластичность венозных и артериальных сосудов соответственно ;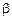 – насосный коэффициент сердца.
– насосный коэффициент сердца.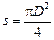 ,
,
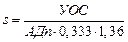 ,
,
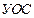 – ударный объем сердца;
– ударный объем сердца;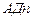 – пульсовое артериальное давление;
– пульсовое артериальное давление;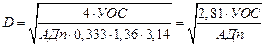 .
.